Механика электропривода
Какие моменты и силы действуют в системе при пуске, торможении, установившемся движении?
Что
определяет время переходных процессов
,
i(t),
их характер?
В основе анализа лежит уравнение движения ЭП.
Вывод уравнения.
П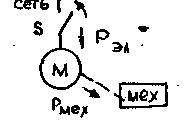
ри
включении М энергия с вала двигателя
Wq
поступает на механизм, часть идет на
полезную работу (преодоление сопротивления
Wс),
а часть запасается в виде кинетической
энергии Wj.
Баланс энергии имеет вид:
W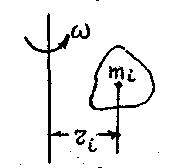
q=Wc
+ Wj
(Дж), где
W
поступательное
движение;
W
-вращательное
движение,
где J –момент инерции;
J=
,
где m
- масса, г - радиус вращения. V
и
-
скорость поступательного и вращательного
движения.
С
учетом того, что мощность Р =
(Вт),
уравнение энергии можно выразить:
Pd
= Pc+P
,
где Pj
= J
или Pj
=mV
.
Момент равен: M=
.
Если уравнение мощности разделить на
,
то получим: Мд=Мс
+ Mj,
где Mj
= J
.
Уравнение это можно записать в виде: МД – МС = J . Mj-инамический момент, который определяется алгебраической суммой моментов двигателя и сопротивления, обеспечивает изменение уровня кинетической энергии.
Следовательно режим работы ЭП обусловлен соотношением движущего момента Мд и момент сопротивления Мс. Если: Мд > Мс, > 0- разгон; Мд< Мс, < 0 — торможение; Мд = Мс, = 0 - установившееся движение.
Н
а
рис даны механические характеристики
двигателя АД
(Мд)
и механизма
(Мс).
Для удобства характеристика механизма
перенесена в 1 четверть
(-Мс).
Так как в момент пуска (
=0)
момент двигателя Мп > Мс, из уравнения
моментов
> 0, т.е. начинается разгон. Наибольшее
ускорение будет при Mjmax,
где динамический момент достигает
максимального значения. В т.А наступит
установившейся режим работы
;
Мд=Мс.
Переходный процесс при пуске (t) имеет вид на рисунке.
В
общем случае Мд и Мс могут быть направлены
согласно или против вращения.
С
учетом сказанного уравнение движения
можно записать:
=J
.
Правило знаков: если момент совпадает по направлению со скоростью «+», встречно «–».
а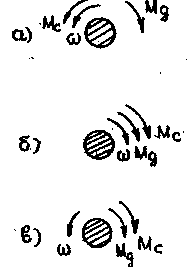
)
–
Мд + Мс =J
;
если Мс Мд – разгон;
если Мд Мс – торможение;
если Мд = Мс – установившееся движение.
б) Мд+Мс=J ; только разгон.
в) –Мд-Мс= J - только торможение.
Время
переходного процесса рассчитывается
из выражения уравнения движения: t=J
.
В общем виде Мд
и Мс
зависимы от
.
В ряде случаев это нелинейная зависимость,
что представляет значительные трудности
при расчете. Для оценки времени с
определенной погрешностью Мд,
Мс
на нелинейных участках спрямляют или
делают постоянными, что позволяет
перейти к алгебраическим методам
расчета. Механические характеристики
разбивают на участки, находят время
переходного процесса
;
для каждого участка. Сумма
представляет время переходного процесса.
П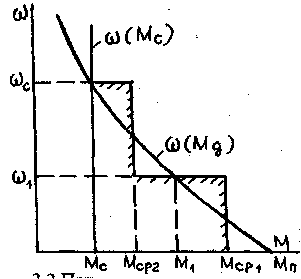
ример.
Дана механическая характеристика
двигателя ω(Мд) и механизма ω(Мс). Пуск
разбиваем на два участка: 1) от 0 до ω1
где
,
2)
от ω1
до ωс,
где
.
Время
первого участка
;
на втором
.
Время
пуска:
.
Приведение статических моментов и моментов инерции к одной оси.
Уравнение движения справедливо для оси, где все элементы механизма вращаются с одинаковой скоростью. В реальных системах оси вращаются с различными скоростями, которые определяются передаточными числами и соотношениями рычагов. Для составления уравнения движения кинематику системы сводят к одной оси, которая вращается со скоростью двигателя, имеет приведенный момент инерции JI и приведенный момент сопротивления МсI.
На этой же оси действует и момент двигателя Мд.
На рис дана схема лебедки и ее схема замещения:
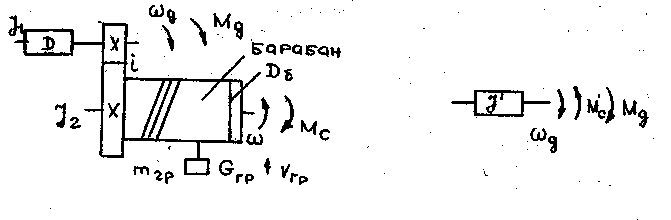
Здесь i - передаточное число; j1 и j2 - моменты инерции оси двигателя и барабана, Gгр и mгр - вес и масса груза. В основе приведения лежит закон сохранения энергии. Момент на оси барабана: МC = Grp · Dб/2.
Приведенный
статический момент к оси двигателя МСI
равен:
,
;
с учетом
;
.
Трение в редукторе или других передачах требует коррекции МCI.
При
подъеме и горизонтальном движении
,
- КПД редуктора.
При
спуске
.
Приведенный момент инерции jI должен запасать такое же количество энергии, как и вся система.
;
.
Разделив
получим:
.
Последнее слагаемое это приведение поступательно движущейся массы.
В
общем виде:
.
С
учетом приведения уравнение движения
имеет вид:
.