Момент импульса в квантовой механике[править | править исходный текст] Оператор момента[править | править исходный текст]

В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определенными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на   (  с чертой), определяемой, как постоянная Планка, поделенная на  . Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновой момент импульса всегда кратен  . Например, электрон в состоянии покоя имеет момент импульса  .^{[источник не указан 138 дней]}

В классическом определении момент импульса зависит от 6 переменных  ,  ,  ,  ,  , и  . Переводя это на квантов механические определения, используя принцип неопределенности Гейзенберга, получаем, что невозможно вычислить все шесть переменных одновременно с любой точностью. Поэтому есть ограничение на то, что мы можем узнать или подсчитать о практическом моменте импульса. Это значит, что лучшее, что мы можем сделать — это подсчитать одновременно величину вектора момента импульса и его компоненты по осям.

Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции:

где   и   — координатный и импульсный оператор, соответственно, а второй — на внутренние, спиновые. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как:

где   — оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная, она имеет следующие свойства:

, где   — Символ Леви-Чивиты;

и даже более важные подстановки с гамильтонианом частицы без заряда и спина:

Симметрия вращения[править | править исходный текст]

Операторы момента импульса обычно встречаются при решении задач сферической симметрии в сферических координатах. Тогда момент импульса в пространственном отображении:

Когда находят собственные значения этого оператора, получают следующее:

где

— сферические функции.

Вычисление момента импульса в нерелятивистской механике[править | править исходный текст]

Если имеется материальная точка массой  , двигающаяся со скоростью   и находящаяся в точке, описываемой радиус-вектором  , то момент импульса вычисляется по формуле:

где   — знак векторного произведения.

Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки и векторно просуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл:

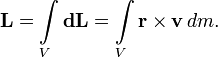
Можно переписать это через плотность  :

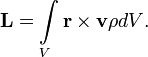
(Если считать, что   — обобщенная функция, включающая, возможно, и дельтообразные члены, то последняя формула применима и к распределенным, и к дискретным системам).

Для систем, совершающих вращение как целое (как абсолютно твёрдое тело) вокруг одной из осей симметрии (или, обобщенно — вокруг так называемых главных осей инерции тела), справедливо соотношение

где   — момент инерции относительно оси вращения,   — вектор угловой скорости.

В общем случае вектор момента связан с вектором угловой скорости через линейный оператор момента инерции (тензор инерции):

Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси: суммарный момент сил, действующих на тело, равен произведению момента инерции тела на угловое ускорение:  . Учитывая, что момент импульса твердого тела  , уравнение динамики твердого тела можно представить в виде .