Вычисление момента[править | править исходный текст]

Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам   и  . Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения. Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на неё можно указать ряд рецептов в соответствии с общими правилами нахождения векторного произведения двух векторов.

где   — угол между   и  , определяемый так, чтобы поворот от   к   производился против часовой стрелки с точки зрения наблюдателя, находящегося на положительной части оси вращения. Направление поворота важно при вычислении, так как определяет знак искомой проекции.

Запишем   в виде  , где   — составляющая радиус-вектора, параллельная вектору импульса, а   — аналогично, перпендикулярная ему.   является, по сути, расстоянием от оси вращения до вектора  , которое обычно называют «плечом». Аналогично можно разделить вектор импульса на две составляющие: параллельную радиус-вектору   и перпендикулярную ему  . Теперь, используя линейность векторного произведения, а также свойство, согласно которому произведение параллельных векторов равно нулю, можно получить ещё два выражения для  .

Сохранение углового момента[править | править исходный текст]

Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой неподвижной точки (или сумма моментов относительно любой неподвижной оси) для замкнутой системы остается постоянной со временем.

Производная момента импульса по времени есть момент силы:

Таким образом, требование замкнутости системы может быть ослаблено до требования равенства нулю главного (суммарного) момента внешних сил:

где   — момент одной из сил, приложенных к системе частиц. (Но конечно, если внешние силы вообще отсутствуют, это требование также выполняется).

Математически закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол  , радиус-вектор частицы с номером  изменятся на  , а скорости —  . Функция Лагранжа  системы при таком повороте не изменится, вследствие изотропии пространства. Поэтому

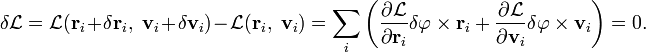
С учетом  , где   — обобщенный импульс  -той частицы, каждое слагаемое в сумме из последнего выражения можно переписать в виде

Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:

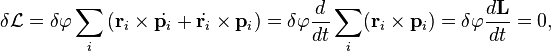
где,   — момент импульса системы. Ввиду произвольности  , из равенства   следует  .

На орбите момент импульса распределяется между моментами импульса собственного вращения планеты и её орбитального движения:

Момент импульса в электродинамике[править | править исходный текст]

При описании движения заряженной частицы в электромагнитном поле, канонический импульс   не является инвариантным. Как следствие, канонический момент импульса   тоже не инвариантен. Тогда берем реальный импульс, который также называется «кинетическим импульсом»:

где   — электрический заряд,   — скорость света,   — векторный потенциал. Таким образом, гамильтониан (инвариантный) заряженной частицы массы   в электромагнитном поле:

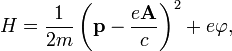
где   — скалярный потенциал. Из этого потенциала следует закон Лоренца. Инвариантный момент импульса или «кинетический момент импульса» определяется: