Центростреми́тельная си́ла — это название той составляющей действующих на тело сил, которая заставляет тело поворачивать (то есть двигаться по траектории, радиус кривизны которой в точке, где находится тело, не может быть принят равным бесконечности). Это составляющая, направленная перпендикулярно мгновенному вектору скорости тела.

Для образования траектории с радиусом кривизны в данной точке  , центростремительная сила  , где   — центростремительное ускорение в данной точке,   — масса тела,   — его скорость в данной точке, а   — его угловая скорость в данной точке

Центростремительная сила F поворачивает тело массой m, движущееся со скоростью V вокруг точки O по круговой траектории радиуса r

Физический смысл[править | править исходный текст]

Если обратить внимание на поворот траектории тела, можно выделить ускорение  , перпендикулярное скорости. Именно это ускорение изменяет направление движения тела, поворачивая траекторию, и для образования кривизны радиуса   на скорости   это ускорение должно быть равно  , или, что то же самое,  , где   — угловая скорость тела в данной точке относительно мгновенного центра поворота (связь между первой формулой и второй очевидна, учитывая что  ). Эта составляющая ускорения называется центростремительным ускорением. Согласновторому закону Ньютона, наблюдаемое ускорение тела соответствует сумме действующих на него сил. Это верно в инерциальных системах отсчёта, а согласно принципу Д’Аламбера это, при введении соответствующих сил инерции, верно и в неинерциальных. Составляющая действующих на тело сил, соответствующая центростремительному ускорению, называется центростремительной силой ( ).

Центростремительная сила не является самостоятельной силой и представляет собой лишь результат формального разложения суммы всех действующих на тело сил на две составляющие — вдоль и поперёк касательной к траектории движения. В случае установившегося (то есть при постоянной угловой скорости) движения тела по круговой траектории за счёт единственной силы, действующей в направлении центра вращения (например, силы натяжения нити, связывающей тело с центром, или при движении по круговой орбите в поле силы гравитации), вся эта сила является центростремительной. Она направлена перпендикулярно к вектору скорости, работы за полный круг не совершает, кинетическая энергия тела не изменяется. Такое движение может продолжаться неограниченно долго.

В общем случае, при движении по любой траектории, отличающейся от круговой, центр поворота не лежит на направлении суммы действующих на тело сил. Так, например, при движении Земли вокруг Солнца по своей эллиптической орбите, действующая на Землю сила взаимного тяготения Земли и Солнца полностью становится центростремительной лишь вафелии и перигелии. При этом тангенциальная составляющая силы реакции связи, совершает работу, ведущую к увеличению кинетической энергии тела (при разгоне) или уменьшению её (при торможении). Это периодически имеет место во Вселенной при движении небесных тел по кеплеровским эллиптическим орбитам вокруг общего центра тяготения, поскольку работа сил связи за полный оборот равна нулю. Так же, за счёт систематического опережения мгновенного центра вращения смещением точки приложения силы, раскручивают, например, пращу.

Так же как скорости, ускорения и траектории тел зависят от выбранной системы отсчёта, от выбора системы отсчёта зависит и то, какую часть суммы сил понадобится считать центростремительной. В частности, переходя в систему отсчёта, связанную непосредственно с движущимся телом, мы естественным образом сводим траекторию в неподвижную точку в центре системы отсчёта, и, соответственно, не можем в контексте этой системы отсчёта говорить ни о центростремительном ускорении данного тела, ни о соответствующей силе. И наоборот, перейдя в систему отсчёта, вращающуюся относительно тел, мы в ней получаем криволинейные траектории этих тел, соответствующие центростремительные ускорения и, соответственно, центростремительные силы.

С понятием «центростремительная сила» и переходом из инерциальной системы отсчёта во вращающуюся неинерциальную, тесно связано понятие «центробежная сила».

В связи со сложностью понимания переходов из одной системы отсчёта в другую, особенно если они движутся относительно друг друга с динамически меняющимся ускорением, понятия центростремительной и центробежной сил вызывают многочисленные споры и недоразумения.

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:

Если тело вращается вокруг неподвижной оси с угловой скоростью  , то линейная скорость i-ой точки равна  , где  , - расстояние от этой точки до оси вращения. Следовательно.

(5.11)

где   - момент инерции тела относительно оси вращения.

В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости   центра инерции тела, и вращения с угловой скоростью  вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

(5.12)

где   - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.

Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.

Основные кинематические характеристики вращательного движения тела — его угловая скорость ( ) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:

и кинетическая энергия

где I_z — момент инерции тела относительно оси вращения.

Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I₁, I₂ и I₃. Вращательная энергия такой молекулы задана выражением

где ω₁, ω₂, и ω₃ — главные компоненты угловой скорости.

В общем случае, энергия при вращении с угловой скоростью   находится по формуле:

, где   — тензор инерции.

Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.

В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.

Как и любой из фундаментальных законов сохранения, закон сохранения импульса связан, согласно теореме Нётер, с одной из фундаментальных симметрий, — однородность пространства.

Вывод в механике Ньютона[править | править исходный текст]

Согласно второму закону Ньютона для системы из N частиц:

где   импульс системы

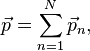
а   — равнодействующая всех сил, действующих на частицы системы

Здесь   — равнодействующая сил, действующим на n-ю частицу со стороны m-ой, а   — равнодействующая всех внешних сил, действующих k-ю частицу. Согласнотретьему закону Ньютона, силы вида   и   будут равны по абсолютному значению и противоположны по направлению, то есть  . Поэтому вторая сумма в правой части выражения (1) будет равна нулю, и получаем, что производная импульса системы по времени равна векторной сумме всех внешних сил, действующих на систему:

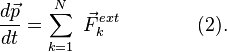
Внутренние силы исключаются третьим законом Ньютона.

Для систем из N частиц, в которых сумма всех внешних сил равна нулю

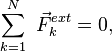
или для систем, на частицы которых не действуют внешние силы   (для всех k от 1 до n), имеем

Как известно, если производная от некоторого выражения равна нулю, то это выражение есть постоянная величина относительно переменной дифференцирования, а значит:

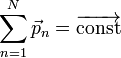 (постоянный вектор).

То есть суммарный импульс системы из N частиц, где N любое целое число, есть величина постоянная. Для N=1 получаем выражение для одной частицы.

Закон сохранения импульса выполняется не только для систем, на которые не действуют внешние силы, но и для систем, сумма всех внешних сил равна нулю. Равенство нулю всех внешних сил достаточно, но не необходимо для выполнения закона сохранения импульса.

Если проекция суммы внешних сил на какую-либо направление или координатную ось равна нулю, то в этом случае говорят о законе сохранения проекции импульса на данное направление или координатную ось.

соответствие некая симметрияуравнений, описывающих систему. В частности, закон сохранения импульса эквивалентен однородности пространства, то есть независимости всех законов, описывающих систему, от положения системы в пространстве. Простейший вывод этого утверждения основан на применении лагранжева подхода к описанию системы.

Вывод из формализма Лагранжа[править | править исходный текст]

Рассмотрим функцию Лагранжа свободного тела   зависящую от обобщённых координат   обобщённых скоростей   и времени t. Здесь точка над qобозначает дифференцирование по времени,   Выберем для рассмотрения прямоугольную декартову систему координат, тогда   для каждой  -той частицы. Используя однородность пространства, мы можем дать всем радиус-векторам частиц одинаковое приращение, которое не будет влиять на уравнения движения:  где   В случае постоянства скорости функция Лагранжа изменится следующим образом:

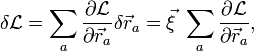
где суммирование идет по всем частицам системы. Так как приращение не влияет на уравнения движения, то вариация функции Лагранжа должна быть равной нулю:   С учётом того, что вектор   — произвольный, последнее требование выполняется при:

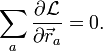
Воспользуемся уравнением Лагранжа 

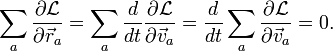
Это означает, что сумма, стоящая под знаком дифференциала, — постоянная величина для рассматриваемой системы. Сама сумма и есть суммарный импульс системы:

.

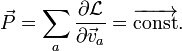Учитывая, что лагранжиан свободной частицы имеет вид:   нетрудно видеть, что последнее выражение совпадает с выражением в ньютоновом формализме:

Для релятивистской свободной частицы лагранжиан имеет несколько другую форму:   что приводит к релятивистскому определению импульса

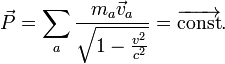
В настоящее время не существует каких-либо экспериментальных фактов, свидетельствующих о невыполнении закона сохранения импульса.