§4. Уравнения первого порядка, не разрешенные относительно производной
Рассмотренные выше уравнения, интегрируемые в квадратурах, были уравнениями, разрешенными относительно производной, либо их можно было представить в таком виде. В данном параграфе будет рассмотрен метод решения некоторых простейших уравнений, не разрешенных относительно производной, то есть уравнений вида
(1)
Иногда
это уравнение удается разрешить
относительно
тогда получаем одно или несколько
уравнений вида
.
(2)
В этом случае интегрируя эти, уже разрешенные относительно производной, уравнения, найдем общее решение исходного уравнения (1).
Пример 10. Проинтегрировать уравнение
(3)
▲ Используя
теорему Виета, разрешим это квадратное
уравнение относительно
:
и
.
Интегрируя каждое из полученных
уравнений, получим соответственно
следующие общие интегралы:
Оба семейства решений удовлетворяют исходному уравнению. Общий интеграл уравнения можно записать в виде одного соотношения
Изобразим картину расположения интегральных кривых уравнения (3) на плоскости (рис.7). Заметим, что через каждую точку плоскости проходят две интегральные кривые по разным направлениям. Это объясняется тем, что дифференциальное уравнение, являясь уравнением второй степени относительно , задает в каждой точке плоскости два направления. ▲
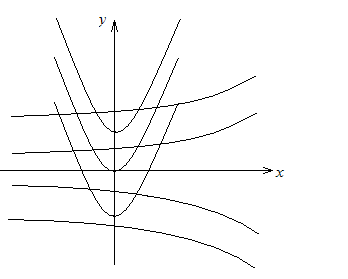
Рис. 7
4.1 Уравнения, не разрешенные относительно производной, но разрешенные относительно аргумента или функции
Однако,
не всегда уравнение (1) можно разрешить
относительно производной, таковы,
например, уравнения
В некоторых случаях к уравнениям вида
(1) применим своеобразный метод решения,
который называется методом
введения параметра.
Этот метод применяется, если уравнение
(1) легко разрешается относительно
переменной
или
,
то есть оно представимо в виде
или
Рассмотрим уравнение вида
(4)
которое является уравнением, неразрешенным относительно производной, но разрешенным относительно искомой функции.
Решение
уравнения.
Данное уравнение интегрируется методом
введения параметра. Обозначим
через
.
Тогда, подставляя
в (4), получим
(5)
Дифференцируем (5) по , учитывая, что зависит от как непосредствен-
но, так и через промежуточную переменную :
Заменяем
через
Разрешая
это уравнение относительно
,
получим уравнение
(6)
Дифференциальное уравнение (6) является уже уравнением, разрешенным относительно производной. Предположим, что уравнение (6) интегрируется в квадратурах и его общий интеграл есть
(7)
Могут представиться два случая:
1)
равенство (7) разрешимо относительно
,
то есть
Тогда, подставляя выражение для
в (5), получим общее решение уравнения
(4) в явном виде
;
(8)
2)
равенство (7) разрешимо относительно
,
то есть
Подставляя значение
в (5), получим
как функцию параметра
:
(9)
В итоге получим общее решение уравнения (4) в параметрическом виде ( – параметр):
Возможность интегрирования уравнения (4) в квадратурах зависит от того будет ли уравнение (6) интегрироваться в квадратурах. ▲
Замечание. Не следует путать метод введения параметра с методом замены переменной, то есть нельзя после нахождения общего интеграла (7) вместо параметра в (7) подставлять и далее находить интегрированием, так как равенство (7) есть общий интеграл уравнения (6), которое получено из исходного уравнения (4) не заменой, а дифференцированием его.
Аналогичными
рассуждениями, используя метод введения
параметра, решаются уравнения:
Пример 11. Решить уравнение
.
(10)
▲ Данное уравнение вида (4), поэтому для его интегрирования используем метод введения параметра. Обозначим через . Подставляя в (10), получим
.
(11)
Дифференцируем (11) по , учитывая, что зависит от как непосредственно, так и через промежуточную переменную :
.
В результате преобразований приходим к уравнению
,
которое распадается на два уравнения:
.
Общее
решение первого уравнения:
.
Подставляя это значение
в
(11), получаем общее решение исходного
уравнения:
.
Из второго уравнения получаем:
.
Если подставить это значение
в (11),
то
получим функцию
,
которая является еще одним решением
исходного уравнения, не входящим в его
общее решение. ▲