
- •Змістовий модуль 4. Пряма лінія на площині. Способи задання. Різні рівняння прямої
- •1. Основні теоретичні відомості Рівняння лінії на площині
- •Рівняння прямої на площині
- •Кут між прямими. Умова перпендикулярності
- •Взаємне розташування прямих і точок відносно прямих. Умова паралельності
- •Нормальне рівняння прямої. Відстань від точки до прямої. Рівняння бісектрис кутів між двома прямими
- •Пучок прямих на площині
- •2. Питання для самоперевірки
- •3. Методичні вказівки до розв’язування задач
- •4. Завдання для самостійної роботи
- •5. Завдання для контрольної роботи
- •Література
4. Завдання для самостійної роботи
1.
Знайти відстань
від точки
![]() до прямої, яка проходить через точки
до прямої, яка проходить через точки
![]() .
.
2. Написати рівняння прямої:
яка проходить через точки
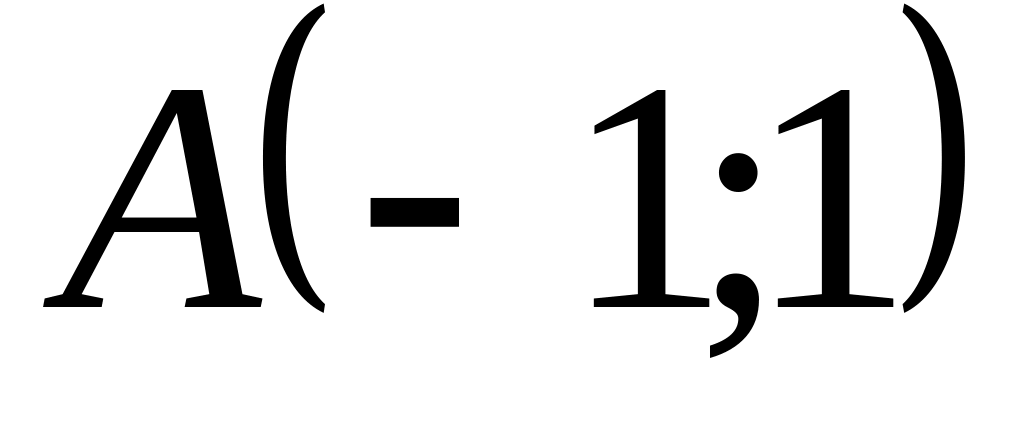 і
і
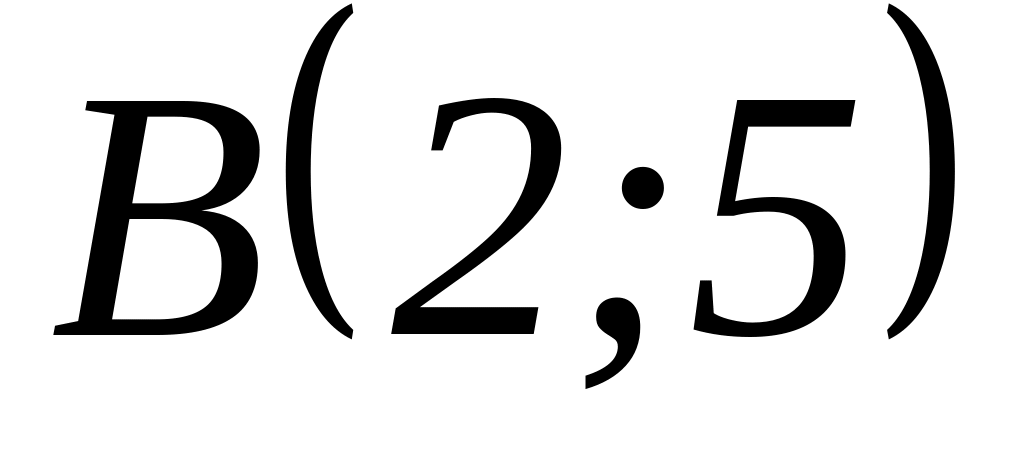 ;
;яка проходить через початок координат і точку
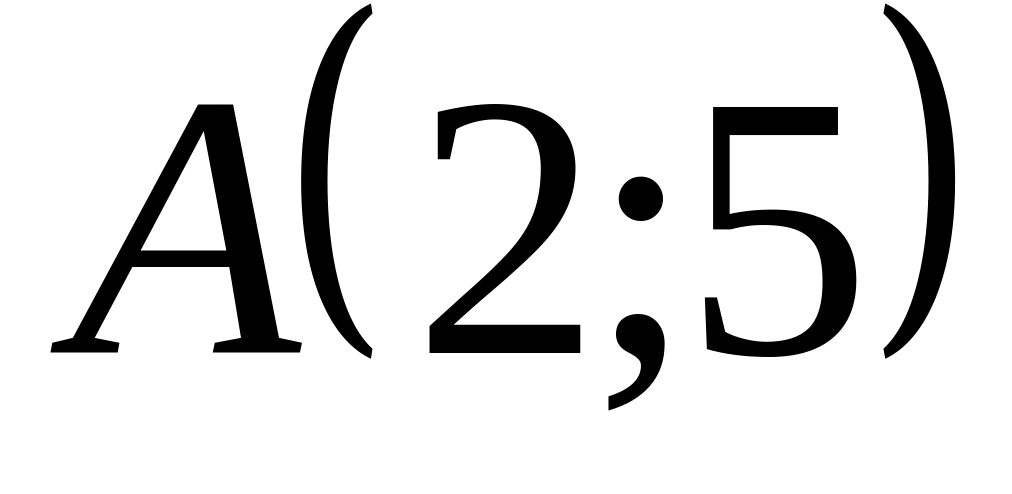 ;
;яка проходить через точку
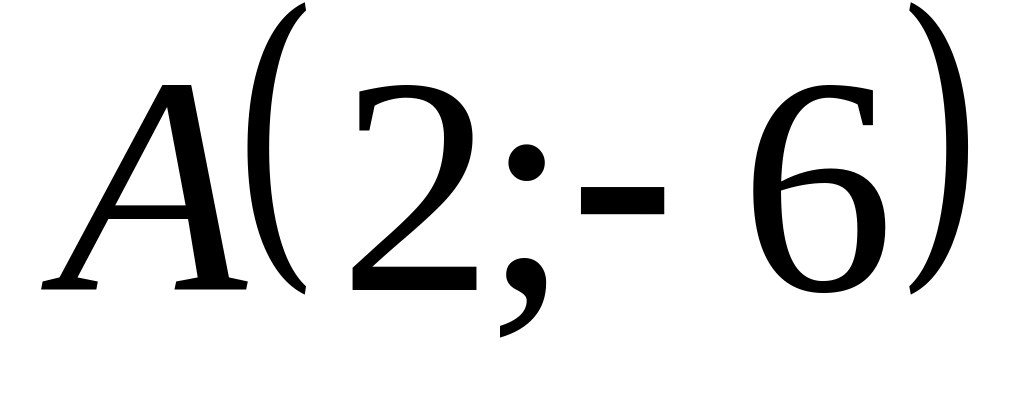 і паралельна вектору
і паралельна вектору
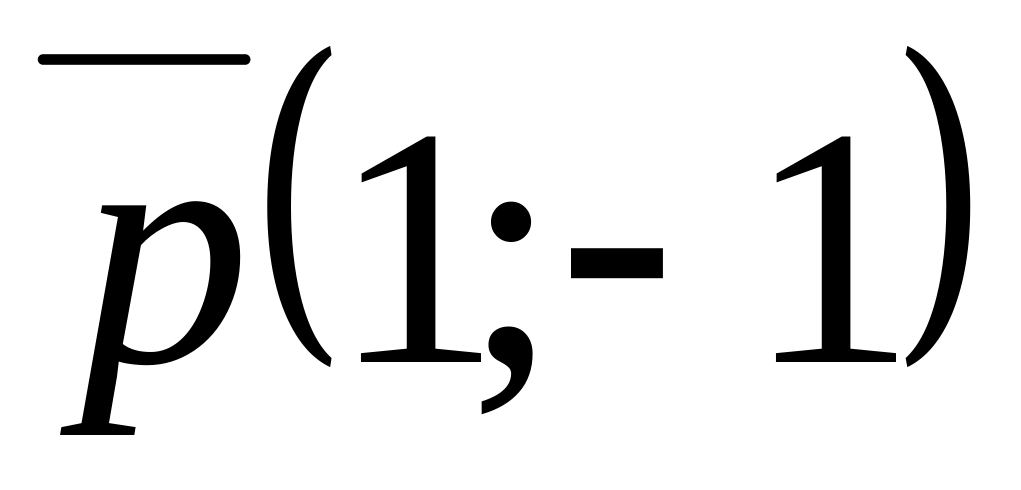 ;
;яка відтинає на осях координат відрізки
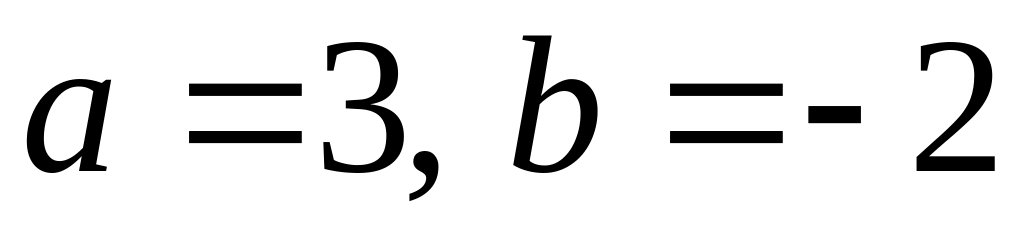 ;
;яка проходить через точку
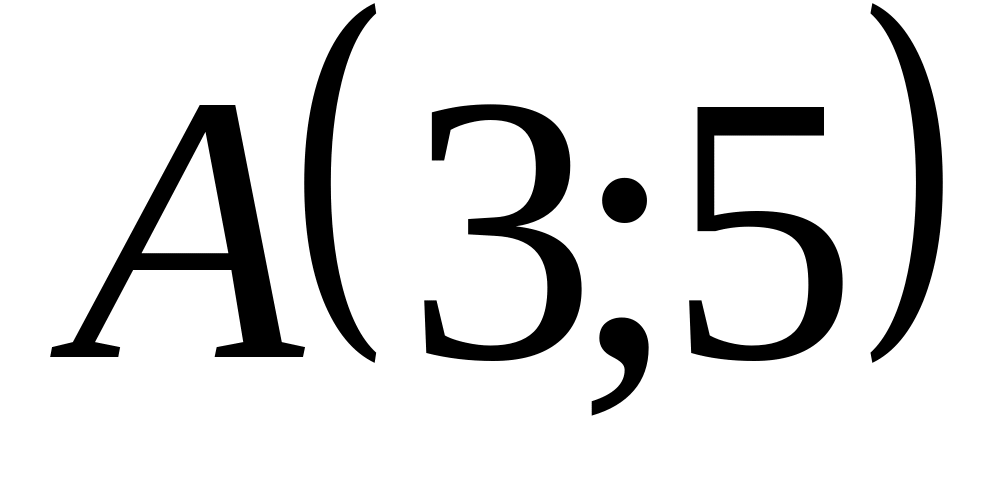 і паралельна осі
;
і паралельна осі
;яка проходить через точку
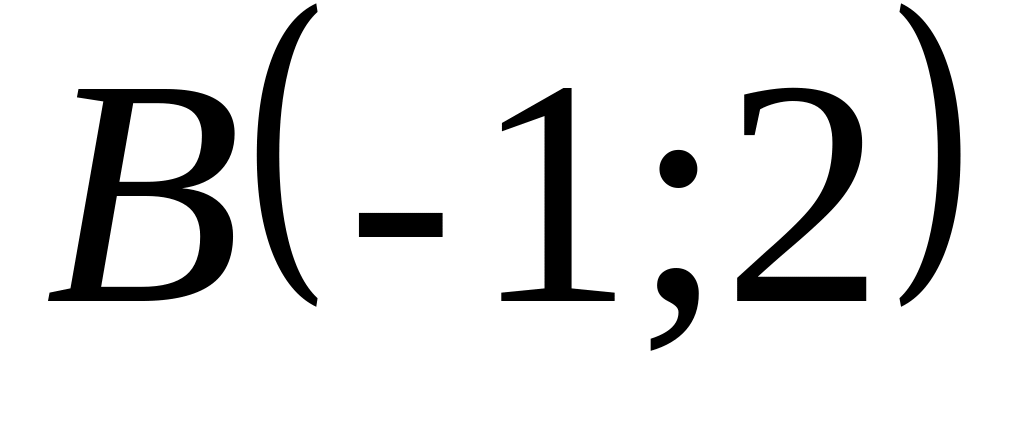 і паралельна осі
;
і паралельна осі
;яка проходить через точку
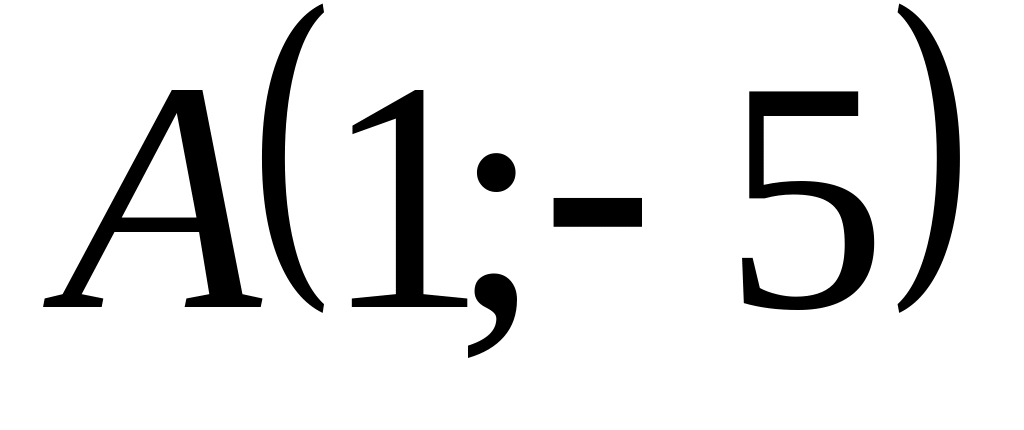 і паралельна прямій
і паралельна прямій
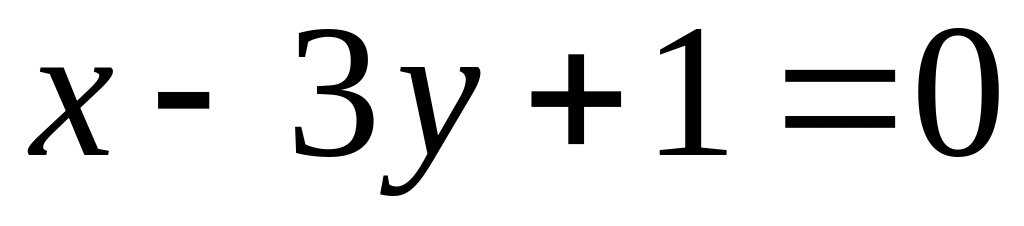 ;
;яка проходить через точку
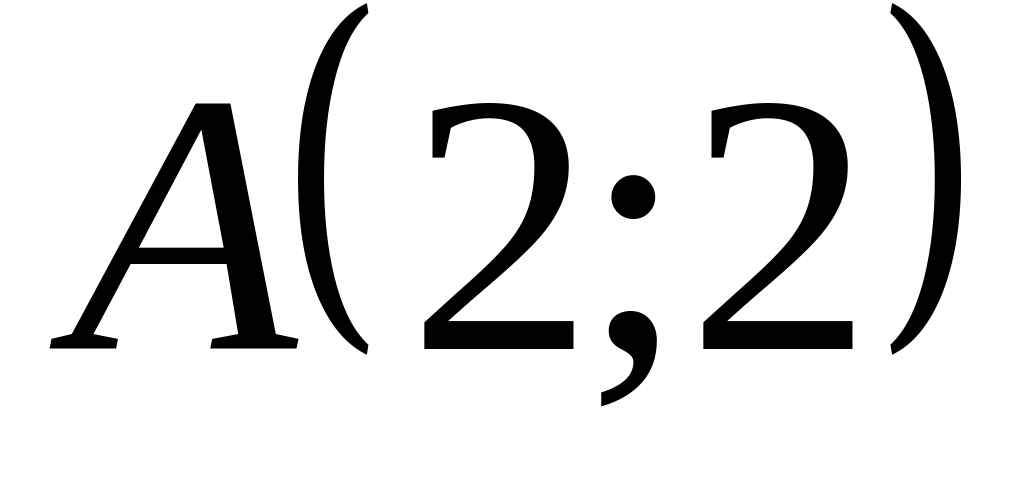 і паралельна прямій
і паралельна прямій
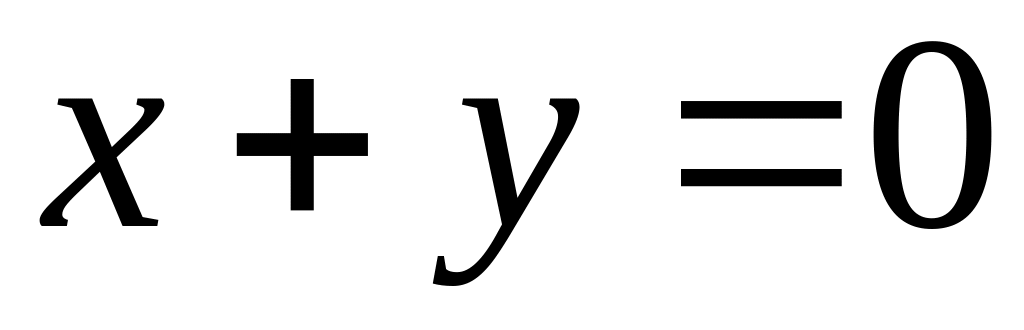 .
.
3.
Показати, що чотирикутник
![]() ,
де
,
де
![]() і
і
![]() ,
є трапецією. Скласти рівняння середньої
лінії та діагоналей цієї трапеції.
,
є трапецією. Скласти рівняння середньої
лінії та діагоналей цієї трапеції.
4.
Дано суміжні вершини
![]() і
і
![]() паралелограма
і точка
перетину його діагоналей. Скласти
рівняння сторін паралелограма.
паралелограма
і точка
перетину його діагоналей. Скласти
рівняння сторін паралелограма.
5.
Дано рівняння двох суміжних сторін
паралелограма
![]() і
та точка перетину його діагоналей
і
та точка перетину його діагоналей
![]() .
Написати рівняння двох інших сторін
паралелограма.
.
Написати рівняння двох інших сторін
паралелограма.
6. Написати рівняння прямої:
яка проходить через точку і має кутовий коефіцієнт
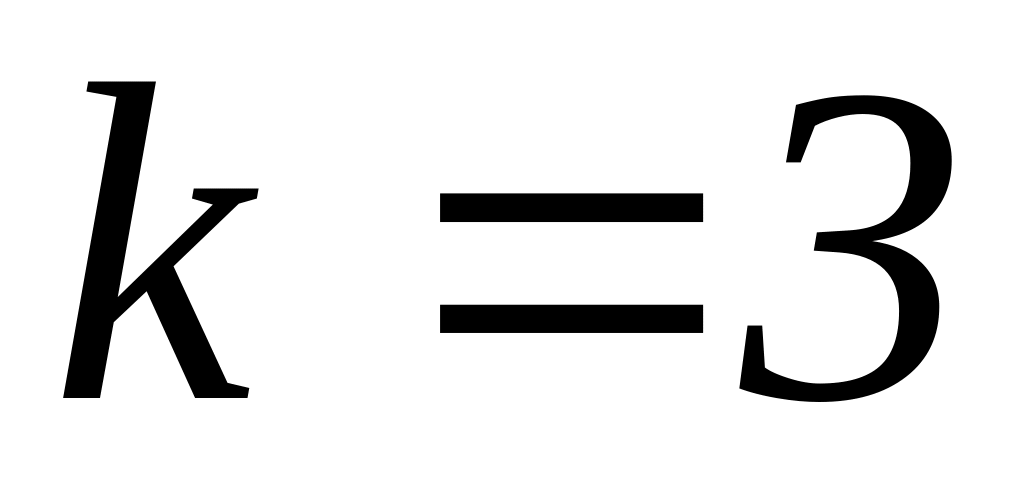 ;
;яка проходить через початок координат і має кутовий коефіцієнт
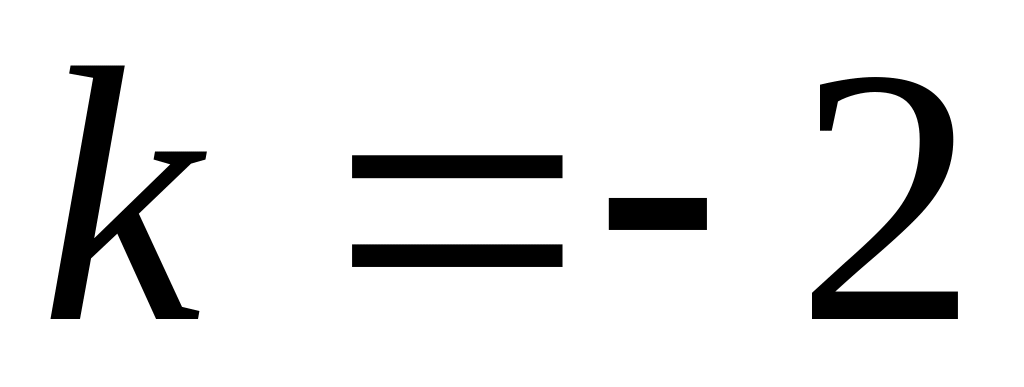 ;
;яка є бісектрисою координатного кута
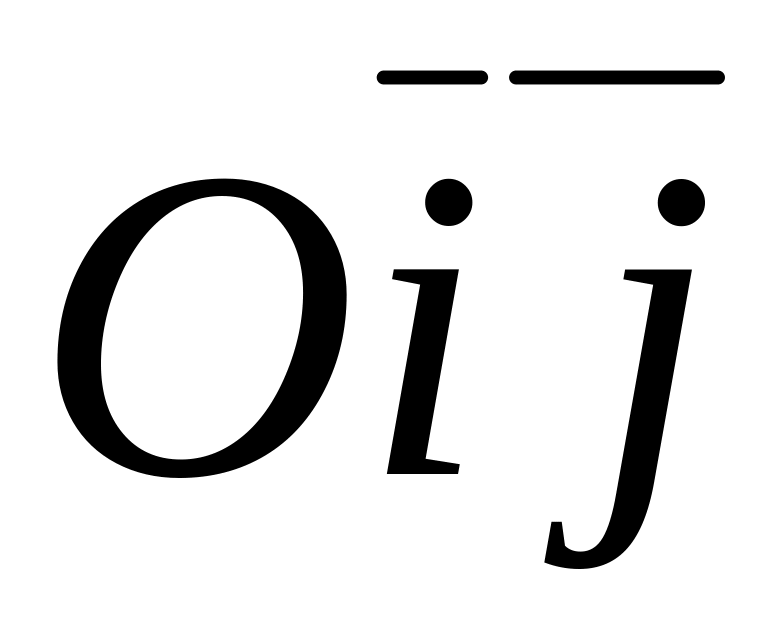 ;
;яка проходить через початок координат і утворює з віссю кут
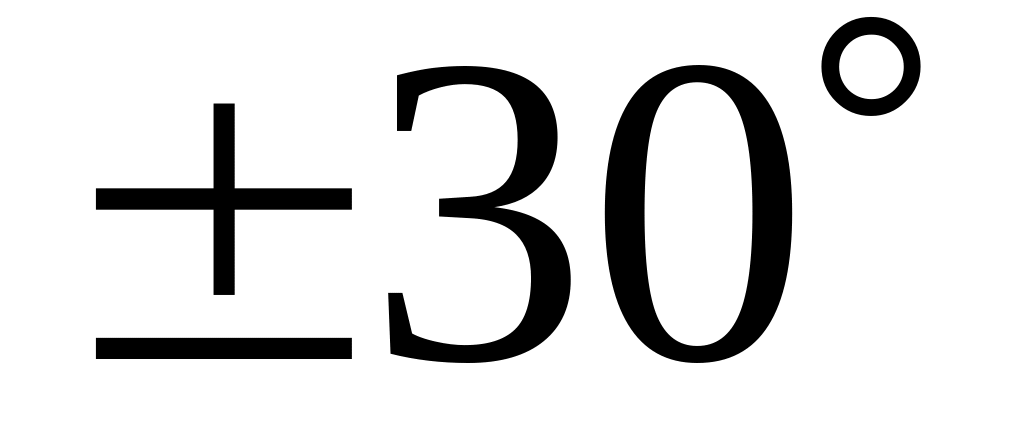 ;
;яка проходить через початок координат і утворює з віссю кут
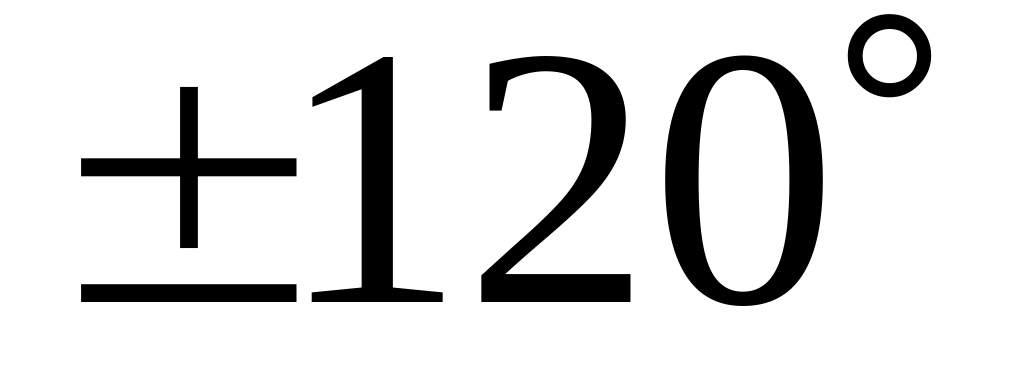 ;
;яка відтинає від осі відрізок
 і має кутовий коефіцієнт
.
і має кутовий коефіцієнт
.
7. Написати рівняння прямої:
яка проходить через точку
 і перпендикулярна до вектора
і перпендикулярна до вектора
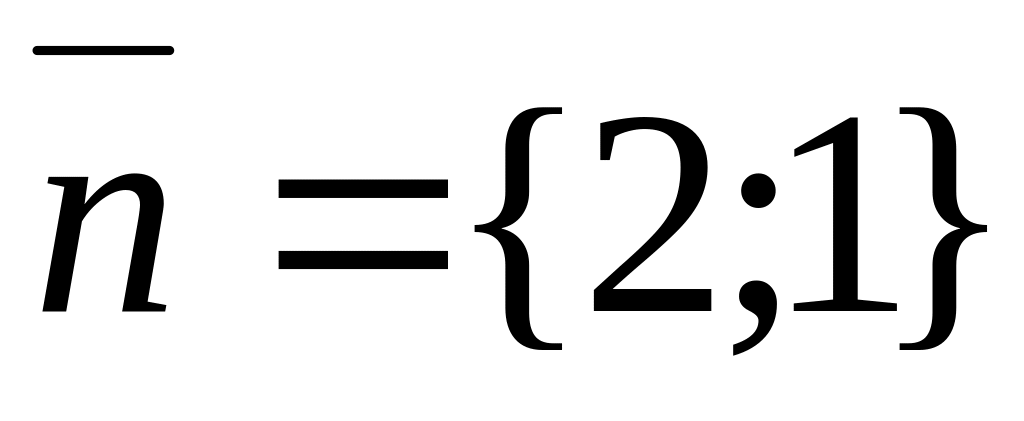 ;
;яка проходить через точку
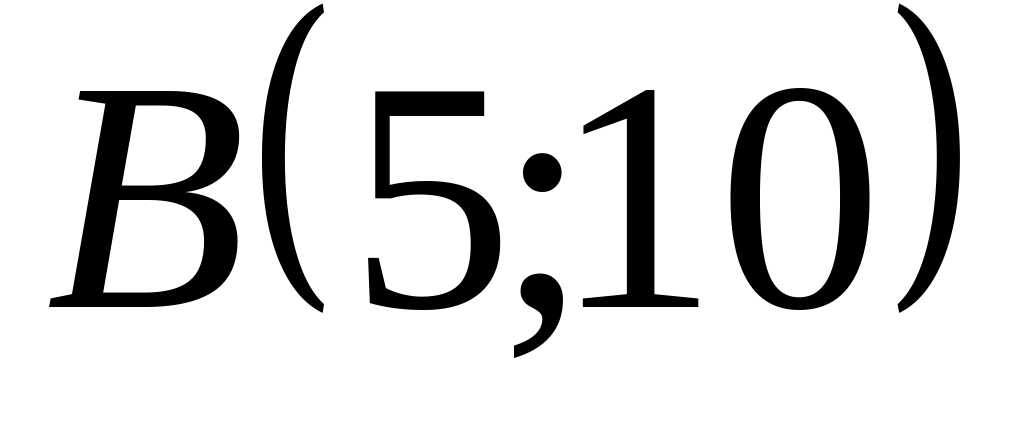 і перпендикулярна до прямої
і перпендикулярна до прямої
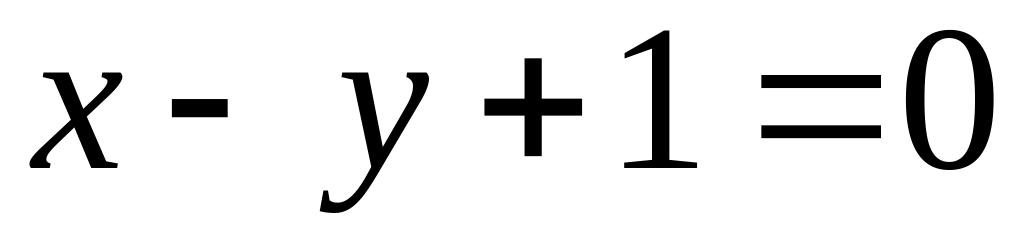 ;
;яка проходить через початок координат і перпендикулярна до прямої
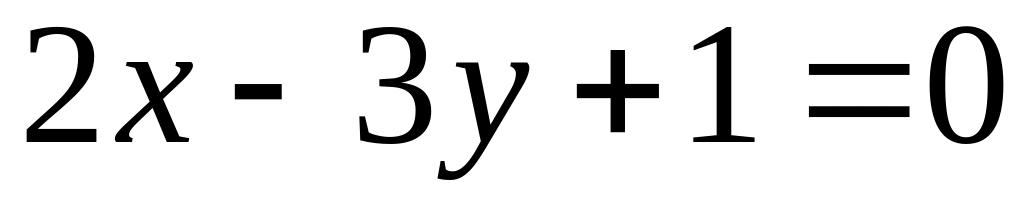 .
.
8.
На прямій
![]() знайти точку, рівновіддалену від точок
знайти точку, рівновіддалену від точок
![]() і
і
![]() .
.
9.
Дано дві вершини трикутника
![]() ,
,
![]() і точка
і точка
![]() перетину його висот. Скласти рівняння
його сторін.
перетину його висот. Скласти рівняння
його сторін.
10.
Визначити координати точки, яка симетрична
точці
![]() відносно прямої
відносно прямої
![]() .
.
11.
Вершини трикутника знаходяться в точках
![]() .
Написати рівняння.
.
Написати рівняння.
бісектриси внутрішнього кута ;
медіани, яка проходить через вершину ;
висоти, яка опущена з вершини .
12.
Обчислити координати вершин ромба, якщо
відомі рівняння двох його сторін:
![]() і
і
![]() та рівняння однієї з його діагоналей
та рівняння однієї з його діагоналей
![]() .
.
13.
Скласти рівняння сторін трикутника
![]() ,
якщо дана одна з його вершин
,
якщо дана одна з його вершин
![]() і рівняння двох медіан
і рівняння двох медіан
![]() і
і
![]() .
.
14.
Скласти рівняння сторін трикутника
,
якщо дана одна з його вершин
![]() і рівняння двох висот
і рівняння двох висот
![]() і
і
![]() .
.
15.
Скласти рівняння сторін трикутника
,
знаючи одну з його вершин
![]() і рівняння двох бісектрис
і
і рівняння двох бісектрис
і
![]() .
.
16.
Обчислити площу ромба, якщо відома його
вершина
![]() ,
точка
,
точка
![]() ,
яка лежить на стороні
,
яка лежить на стороні
![]() ,
і
точка
,
і
точка
![]() перетину
його діагоналей.
перетину
його діагоналей.
17.
Дано рівняння однієї зі сторін квадрата
![]() і точка перетину діагоналей
і точка перетину діагоналей
![]() .
Скласти рівняння його діагоналей і
інших сторін. Визначити координати
вершин квадрата.
.
Скласти рівняння його діагоналей і
інших сторін. Визначити координати
вершин квадрата.
18.
Промінь світла спрямований по прямій
![]() .
Дійшовши до прямої
,
він відбився. Скласти рівняння прямої,
на якій лежить відбитий промінь.
.
Дійшовши до прямої
,
він відбився. Скласти рівняння прямої,
на якій лежить відбитий промінь.
19.
Дано рівняння основи рівнобедреного
трикутника
і його бічної сторони
.
Скласти рівняння другої бічної сторони,
якщо вона проходить через точку
![]() .
.
20.
Скласти рівняння сторін трикутника,
знаючи одну його вершину
![]() ,
а також рівняння висоти
,
а також рівняння висоти
![]() і бісектриси
і бісектриси
![]() ,
проведених з однієї вершини.
,
проведених з однієї вершини.
21.
Скласти рівняння сторін трикутника,
знаючи одну його вершину
![]() ,
а також рівняння висоти
,
а також рівняння висоти
![]() і бісектриси
і бісектриси
![]() ,
проведених з різних вершин.
,
проведених з різних вершин.
22.
Скласти рівняння сторін трикутника,
знаючи одну його вершину
![]() ,
а також рівняння висоти
,
а також рівняння висоти
![]() і медіани
і медіани
![]() ,
проведених з однієї вершини.
,
проведених з однієї вершини.
23.
Скласти рівняння сторін трикутника,
знаючи одну його вершину
![]() ,
а також рівняння бісектриси
і медіани
,
а також рівняння бісектриси
і медіани
![]() ,
проведених з однієї вершини.
,
проведених з однієї вершини.
24.
Скласти рівняння сторін трикутника,
знаючи одну його вершину
![]() ,
а також рівняння бісектриси
,
а також рівняння бісектриси
![]() і медіани
і медіани
![]() ,
проведених з різних вершин.
,
проведених з різних вершин.
25.
Скласти рівняння прямої, яка проходить
через точку
![]() ,
і відтинає від координатного кута
трикутник із площею, яка рівна 12.
,
і відтинає від координатного кута
трикутник із площею, яка рівна 12.
26.
Знайти довжини висот трикутника, сторони
якого задані рівняннями
![]() .
.
27.
Написати рівняння кола з центром в точці
![]() ,
яке дотикається до прямої
,
яке дотикається до прямої
![]() .
.
28. Знайти рівняння кола, яке концентричне з колом
![]()
і яке дотикається до прямої .
29.
Знайти рівняння кола, яке проходить
через точки
![]() і
і
![]() та дотикається до прямої
та дотикається до прямої
![]() .
.
30. Знайти відстань між паралельними прямими у кожному з наступних випадків:
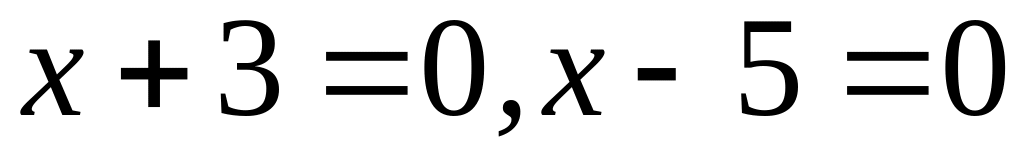 ;
;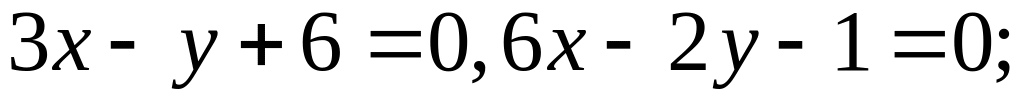
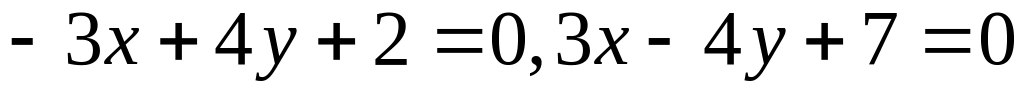 ;
;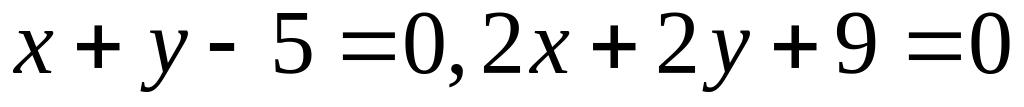 .
.
31.
Через точку
![]() проведена пряма, відстань від якої до
точки
проведена пряма, відстань від якої до
точки
![]() дорівнює 5.
Скласти рівняння прямої.
дорівнює 5.
Скласти рівняння прямої.
32.
Дано квадрат, дві паралельні сторони
якого задані рівняннями
![]() і
і
![]() .
Знайти площу цього квадрата.
.
Знайти площу цього квадрата.
33.
До кола, яке має центр в точці
![]() і радіус, рівний 5,
провести дотичні, паралельні прямій
і радіус, рівний 5,
провести дотичні, паралельні прямій
![]() .
.
34.
Скласти рівняння дотичних до кола
![]() ,
які перпендикулярні прямій
,
які перпендикулярні прямій
![]() .
.
35. Скласти рівняння множини точок, рівновіддалених від двох паралельних прямих:
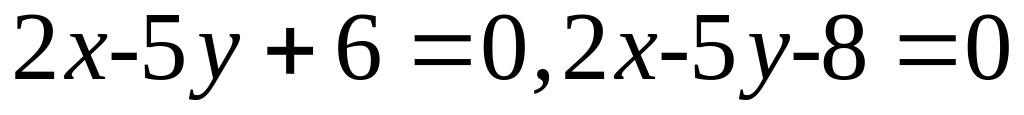 ;
;
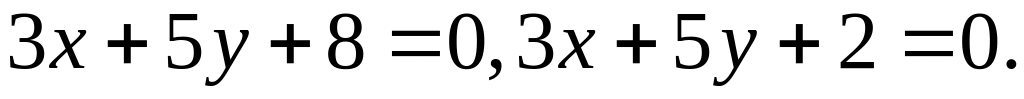
36.
Скласти рівняння бісектриси того кута
між прямими
і
![]() ,
в якому лежить початок координат.
,
в якому лежить початок координат.
37.
Скласти рівняння бісектриси гострого
кута, утвореного прямими
![]() і
і
![]() .
.
38.
Скласти рівняння бісектриси тупого
кута, який утворено прямими
![]() і
і
![]() .
.
39.
Скласти рівняння кола, яке проходить
через точку
![]() і дотикається до прямих
і
і дотикається до прямих
і
![]() .
.
40.
Скласти рівняння кіл, які дотикаються
до паралельних прямих
![]() і
і
![]() та проходять через точку
та проходять через точку
![]() .
.
41.
Написати рівняння прямої, яка проходить
через точку
![]() так, щоб середина її відрізка, який
міститься між двома паралельними прямими
так, щоб середина її відрізка, який
міститься між двома паралельними прямими
![]() ,
,![]() , лежала б на прямій
, лежала б на прямій
![]() .
.
42.
В пучку
![]() знайти пряму, яка проходить через точку
знайти пряму, яка проходить через точку
![]() .
.
43.
В пучку
![]() знайти пряму, паралельну прямій
знайти пряму, паралельну прямій
![]() .
.
44.
В пучку
![]() знайти пряму, яка проходить через початок
координат.
знайти пряму, яка проходить через початок
координат.
45.
Через точку перетину прямих
![]() ,
,
![]() проведена пряма, перпендикулярна до
прямої
.
Написати рівняння цієї прямої.
проведена пряма, перпендикулярна до
прямої
.
Написати рівняння цієї прямої.
46.
Дано рівняння сторін трикутника
![]()
![]() .
Скласти:
.
Скласти:
рівняння висот трикутника;
рівняння прямих, які проходять через вершини трикутника паралельно протилежним сторонам.
47.
Написати рівняння прямої, яка проходить
через точку перетину прямих
![]() і:
і:
паралельна осі ;
паралельна осі ;
проходить через початок координат.
48.
Скласти рівняння прямих, які паралельні
прямій
![]() і віддалених від неї на відстані
і віддалених від неї на відстані
![]() .
.
49.
Дано дві суміжні вершини квадрата
![]() і
і
![]() .
Скласти рівняння його сторін.
.
Скласти рівняння його сторін.
50.
Дано рівняння двох сторін квадрата
![]() і одна з його вершин
і одна з його вершин
![]() .
Скласти рівняння двох інших сторін
цього квадрата.
.
Скласти рівняння двох інших сторін
цього квадрата.
51.
Дано рівняння двох сторін квадрата
![]() .
Скласти рівняння двох інших його сторін
при умові, що точка
.
Скласти рівняння двох інших його сторін
при умові, що точка
![]() лежить на стороні цього квадрата.
лежить на стороні цього квадрата.
52.
Скласти рівняння прямої, яка проходить
через точку
![]() на однакових відстанях від точок
на однакових відстанях від точок
![]() і
і
![]() .
.
53.
На прямій
![]() знайти точки, рівновіддалені від точки
знайти точки, рівновіддалені від точки
![]() та від прямої
та від прямої
![]() .
.
54.
Через точку
проведено пряму так, що її відрізок,
який знаходиться між прямими
і
![]() ,
ділиться в точці
навпіл. Скласти її рівняння.
,
ділиться в точці
навпіл. Скласти її рівняння.
55.
Дано рівняння
![]() двох сторін трикутника і рівняння
двох сторін трикутника і рівняння
![]() однієї з його медіан. Скласти рівняння
третьої сторони.
однієї з його медіан. Скласти рівняння
третьої сторони.
56.
Дано рівняння двох сторін трикутника
![]() ,
,
![]() і точка
і точка
![]() перетину його медіан. Скласти рівняння
третьої сторони і знайти координати
вершин трикутника.
перетину його медіан. Скласти рівняння
третьої сторони і знайти координати
вершин трикутника.
57.
Дано рівняння
![]() двох медіан трикутника і рівняння однієї
з його сторін
двох медіан трикутника і рівняння однієї
з його сторін
![]() .
Скласти рівняння двох інших сторін і
знайти координати його вершин.
.
Скласти рівняння двох інших сторін і
знайти координати його вершин.
58.
Скласти рівняння сторін квадрата, дві
паралельні сторони якого проходять
відповідно через точки
![]() і
і
![]() ,
а дві інші - через точки
,
а дві інші - через точки
![]() і
і
![]() .
.
59.
Через точку
![]() провести пряму так, щоб її відрізок,
який знаходиться між двома даними
прямими
провести пряму так, щоб її відрізок,
який знаходиться між двома даними
прямими
![]() і
і
![]() ,
ділився в точці
навпіл.
,
ділився в точці
навпіл.
60.
Сторони кута, дані своїми рівняннями
і
![]() ,
перетинаються рядом паралельних прямих:
,
перетинаються рядом паралельних прямих:
![]() .
Знайти геометричні місця:
.
Знайти геометричні місця:
середин відрізків паралельних прямих, які знаходяться між сторонами кута;
точок, які ділять у відношенні
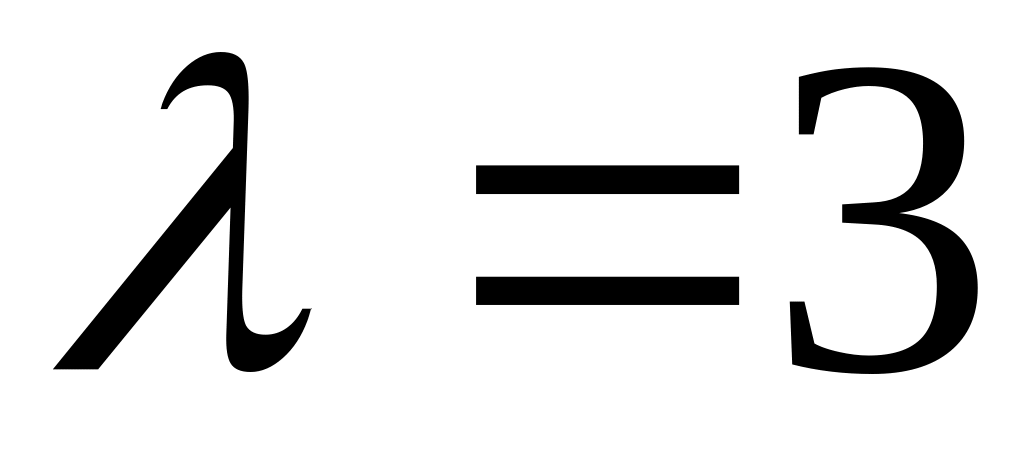 відрізки паралельних прямих, які
містяться між сторонами кута.
відрізки паралельних прямих, які
містяться між сторонами кута.
61.
Знайти центр вписаного кола і центр
ваги рівнобедреного трикутника, якщо
дані рівняння бічних сторін трикутника
![]() ;
;
![]() і точка
і точка
![]() ,
яка лежить на його основі.
,
яка лежить на його основі.
62.
У рівнобедреному трикутнику відоме
рівняння основи
,
рівняння однієї з бічних сторін
![]() і точка
і точка
![]() на іншій бічній стороні. Обчислити :
на іншій бічній стороні. Обчислити :
відстань від бічної сторони до протилежної вершини;
координати центра ваги;
площу трикутника.
63.
Скласти рівняння сторін трикутника,
знаючи одну з його вершин
![]() і рівняння двох висот:
і рівняння двох висот:
![]() і
і
![]() .
.
64.
Скласти рівняння сторін трикутника,
знаючи одну з його вершин
![]() і рівняння двох медіан:
і рівняння двох медіан:
![]() і
і
![]() .
.
65.
Дано трикутник:
![]() і
і
![]() .
Через кінці його медіани
.
Через кінці його медіани
![]() проведені прямі
проведені прямі
![]() і
і
![]() ,
відповідно паралельні двом іншим
медіанам. Перевірити, що сторони
трикутника
,
відповідно паралельні двом іншим
медіанам. Перевірити, що сторони
трикутника
![]() рівні по довжині медіанам трикутника
.
Обчислити відношення площ трикутників
і
.
рівні по довжині медіанам трикутника
.
Обчислити відношення площ трикутників
і
.
66.
Скласти рівняння сторін трикутника,
знаючи одну з його вершин
![]() і рівняння бісектрис двох його кутів:
і
і рівняння бісектрис двох його кутів:
і
![]() .
.
67.
Прямі
![]() і
і
![]() дотикаються до кола, радіус якого
дотикаються до кола, радіус якого
![]() .
Обчислити площу чотирикутника, який
утворено цими дотичними і радіусами
кола, проведеними в точки дотику.
.
Обчислити площу чотирикутника, який
утворено цими дотичними і радіусами
кола, проведеними в точки дотику.
68.
Знаючи вершини трикутника
![]() і
і
![]() ,
перевірити, що висоти його перетинаються
в одній точці, і обчислити площу
трикутника, вершинами якого служать
основи висот даного трикутника
.
,
перевірити, що висоти його перетинаються
в одній точці, і обчислити площу
трикутника, вершинами якого служать
основи висот даного трикутника
.
69.
Дано рівняння сторін трикутника:
![]() і
і
![]() .
Знайти в середині трикутника таку точку,
щоб прямі, які з’єднують її з вершинами
трикутника, розбивали його на три
рівновеликих трикутники.
.
Знайти в середині трикутника таку точку,
щоб прямі, які з’єднують її з вершинами
трикутника, розбивали його на три
рівновеликих трикутники.
70.
Дано рівняння однієї із сторін квадрата
![]() і
точки перетину його діагоналей
і
точки перетину його діагоналей
![]() .
Скласти рівняння його діагоналей
і інших сторін. Визначити координати
вершин.
.
Скласти рівняння його діагоналей
і інших сторін. Визначити координати
вершин.
71.
Дана
вершина
![]() квадрата
і
рівняння прямої
квадрата
і
рівняння прямої
![]() .
Скласти
рівняння прямих, які містять сторони
квадрата.
.
Скласти
рівняння прямих, які містять сторони
квадрата.
72.
Центр
квадрата знаходиться в точці
![]() ,
рівняння
однієї з його
сторін.
,
рівняння
однієї з його
сторін.
![]() .
Скласти
рівняння інших його сторін.
.
Скласти
рівняння інших його сторін.
73.
На прямій
![]() знайти
точку Р,
сума відстаней якої до точок
знайти
точку Р,
сума відстаней якої до точок
![]() була
б найменшою.
була
б найменшою.
74.
Дано
вершини трикутника
:![]() .
Скласти
рівняння перпендикуляра, опущеного з
вершини
на
бісектрису
внутрішнього кута при вершині А.
.
Скласти
рівняння перпендикуляра, опущеного з
вершини
на
бісектрису
внутрішнього кута при вершині А.
75.
Знайти
координати точки, яка симетрична початку
координат відносно
прямої
![]() .
.
76.
Знайти
координати точки, яка симетрична точці
![]() відносно
прямої,
яка проходить через точки
відносно
прямої,
яка проходить через точки
![]()
77.
На
прямій
![]() знайти точку, різниця віддалей якої до
точок
знайти точку, різниця віддалей якої до
точок
![]() та
та
![]() була
б найбільшою.
була
б найбільшою.
78.
На
осі абсцис знайти точку, сума віддалей
якої до точок
![]() та
та
![]() була
б найменшою.
була
б найменшою.
79.
Задано
рівняння двох сторін паралелограма
.
![]() ,
,
![]() і середина
і середина
![]() сторони
сторони
![]() .
Знайти
рівняння двох інших його сторін.
.
Знайти
рівняння двох інших його сторін.
80.
Дано середини
![]() сторін трикутника. Скласти рівняння
його сторін.
сторін трикутника. Скласти рівняння
його сторін.
81.
Скласти рівняння сторін трикутника,
знаючи одну з його вершин
![]() і
рівняння двох його висот:
і
рівняння двох його висот:
![]() і
і
![]()
82. Скласти
рівняння бісектриси того кута між
заданими прямими
![]() і
і
![]() ,
якому належить точка
,
якому належить точка
![]() .
.
83.
Дано дві точки
![]() і
і
![]() .
На осі абсцис знайти таку точку
,
щоб
довжина ламаної
.
На осі абсцис знайти таку точку
,
щоб
довжина ламаної
![]() була
найменшою.
була
найменшою.
84.
Основа рівнобедреного трикутника
належить прямій,
![]() а бічна
сторона – прямій
.
Скласти рівняння іншої бічної сторони,
якщо вона проходить через точку
а бічна
сторона – прямій
.
Скласти рівняння іншої бічної сторони,
якщо вона проходить через точку
![]()
85. Знайти відстань між паралельними прямими: l1: 2x–y+7=0 і l2: 2x–y– –1=0.
86.
До
кола з центром в т.
![]() та радіусом
та радіусом
![]() провести
дотичні паралельні
прямій
провести
дотичні паралельні
прямій
![]() .
.
87.
Промінь
світла направили по прямій
![]() .
Знайти рівняння прямої, на якій лежить
промінь, відбитий від осі абсцис.
.
Знайти рівняння прямої, на якій лежить
промінь, відбитий від осі абсцис.
88.
Дана
пряма
![]() .
Знайти множину точок, рівновіддалених
від цієї прямої на величину
.
Знайти множину точок, рівновіддалених
від цієї прямої на величину
![]() .
.
89.
Скласти
рівняння прямої, яка рівновіддалена
від двох даних паралельних
прямих
![]() і
і
![]() .
.
90.
Дано
рівняння двох сторін квадрата
![]() і
і
![]() і одна
з його вершин
і одна
з його вершин
![]() .
Скласти рівняння двох інших сторін
квадрата.
.
Скласти рівняння двох інших сторін
квадрата.
91.
На
прямій
![]() знайти
точки, рівновіддалені від прямих
знайти
точки, рівновіддалені від прямих
![]() i
i
![]() .
.
92.
Чи перетинає відрізок АВ
з кінцями в точках
і
![]() пряму l,
задану рівнянням
пряму l,
задану рівнянням
![]() ?
Якщо так, то знайти їх точку перетину
?
Якщо так, то знайти їх точку перетину
93.
Скласти
рівняння сторін трикутника, якщо одна
з його вершин
![]() і рівняння двох висот
і рівняння двох висот
![]() і
і
![]() .
.
94.
Обчислити
кут між прямими
![]() і
і
![]() ,
які задані відповідно рівняннями
,
які задані відповідно рівняннями
![]() і
і
![]() .
.
