
- •Змістовий модуль 4. Пряма лінія на площині. Способи задання. Різні рівняння прямої
- •1. Основні теоретичні відомості Рівняння лінії на площині
- •Рівняння прямої на площині
- •Кут між прямими. Умова перпендикулярності
- •Взаємне розташування прямих і точок відносно прямих. Умова паралельності
- •Нормальне рівняння прямої. Відстань від точки до прямої. Рівняння бісектрис кутів між двома прямими
- •Пучок прямих на площині
- •2. Питання для самоперевірки
- •3. Методичні вказівки до розв’язування задач
- •4. Завдання для самостійної роботи
- •5. Завдання для контрольної роботи
- •Література
Пучок прямих на площині
Пучком прямих на площині називається сукупність всіх прямих цієї площини, що проходять через деяку фіксовану точку S, яка називається центром пучка.
Якщо
![]() і
—
рівняння двох різних прямих, які
перетинаються в точці S,
то рівняння
і
—
рівняння двох різних прямих, які
перетинаються в точці S,
то рівняння
![]() (3)
(3)
де
![]() —
довільні дійсні числа, принаймні одне
з яких відмінне від нуля, визначає пряму,
яка належить пучку з центром в точці
S.
І навпаки, для довільної прямої, яка
належить пучку з центром в точці S,
існують такі дійсні числа
,
які не дорівнюють нулю одночасно, що
рівняння (3) є рівнянням цієї прямої.
—
довільні дійсні числа, принаймні одне
з яких відмінне від нуля, визначає пряму,
яка належить пучку з центром в точці
S.
І навпаки, для довільної прямої, яка
належить пучку з центром в точці S,
існують такі дійсні числа
,
які не дорівнюють нулю одночасно, що
рівняння (3) є рівнянням цієї прямої.
Якщо
![]() ,
то, поділивши обидві частини рівняння
(3) на
,
то, поділивши обидві частини рівняння
(3) на
![]() і
поклавши
і
поклавши
![]() ,
отримаємо рівняння
,
отримаємо рівняння
![]()
яке
визначає будь-яку пряму пучка з центром
S,
окрім тієї, яка відповідає значенню
![]() ,
тобто крім прямої
.
,
тобто крім прямої
.
2. Питання для самоперевірки
1. Дайте означення лінії на площині.
2. Що називається кутом нахилу прямої до осі абсцис?
3. Що називається кутовим коефіцієнтом прямої?
4. Чому дорівнює кутовий коефіцієнт прямої в прямокутній декартовій системі координат?
5. Який геометричний зміст мають коефіцієнти k і b у рівнянні прямої з кутовим коефіцієнтом?
6. Які існують способи задання прямої і який буде мати вигляд рівняння прямої відповідно до кожного способу?
7. Який геометричний зміст мають коефіцієнти, що входять до рівняння прямої у відрізках?
8. Який вектор називається нормальним вектором прямої?
9. Як досліджується загальне рівняння прямої? Які існують окремі випадки?
10. Яке рівняння прямої називається неповним?
11. Яке рівняння прямої називається нормальним рівнянням прямої?
12. Для чого використовується нормальне рівняння прямої?
13. Що називається відстанню від точки до прямої?
14. Як знайти відстань від точки до прямої?
15. Як обчислюється кут між двома прямими?
16. Яка умова співпадання двох прямих?
17. Яка умова паралельності і перпендикулярності двох прямих?
18. Що називається пучком прямих, які перетинаються?
19. Які лінії на площині визначають такі рівняння:
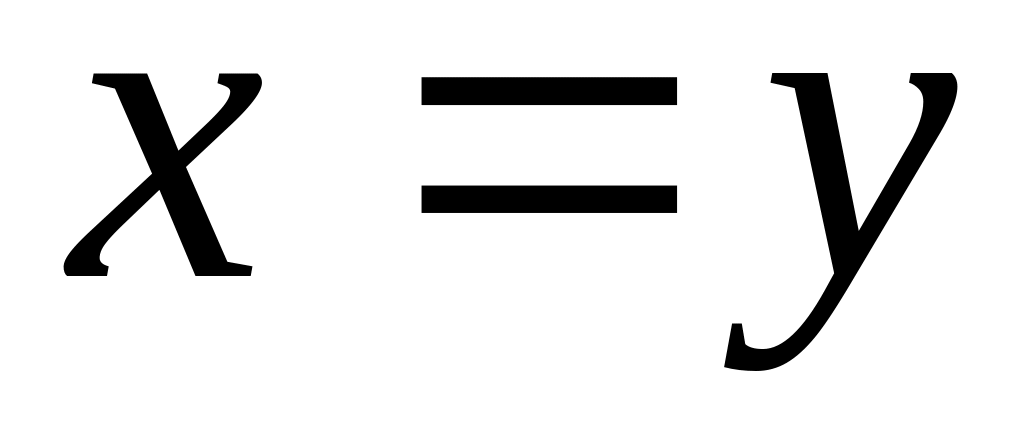 ;
; ;
;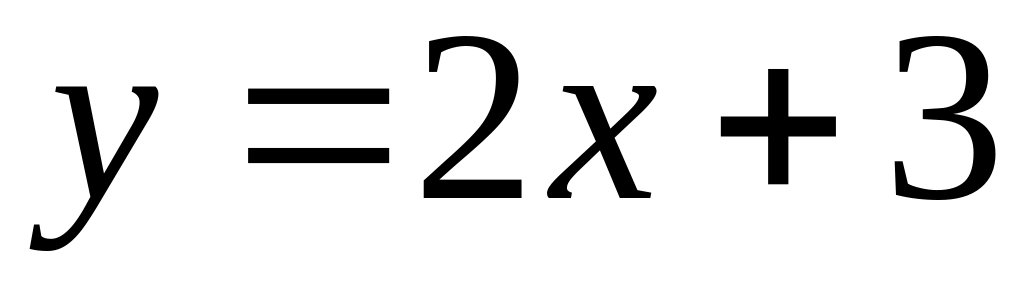 .
.
20. Вкажіть на особливість розміщення прямих, які задані такими рівняннями:
 ;
;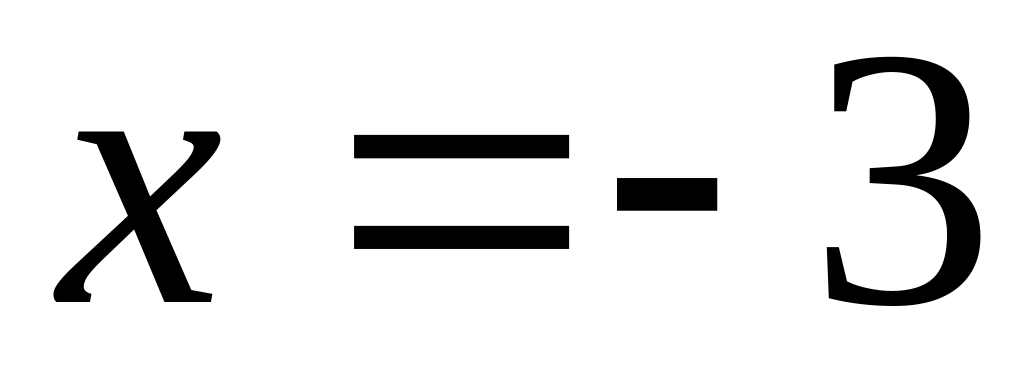 ;
; ;
;;
.
24. Побудувати такі прямі за їх рівняннями:
 ;
; ;
;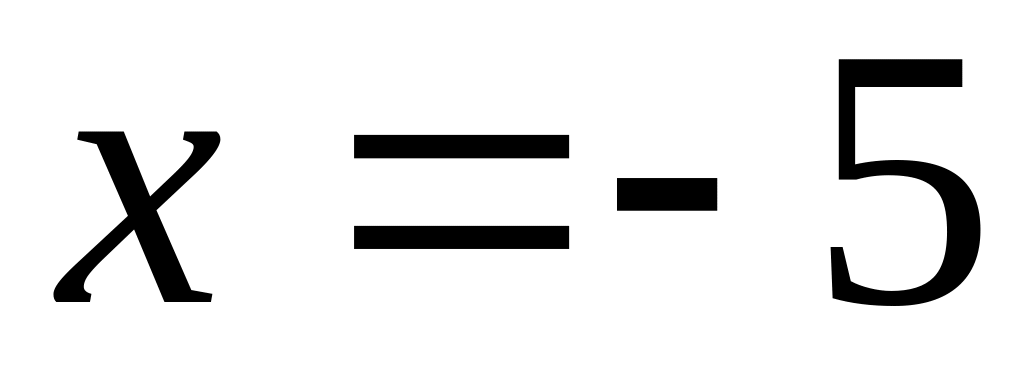 ;
; ;
; .
.
3. Методичні вказівки до розв’язування задач
Задача
1.
Визначити положення відрізка
![]() відносно прямої
відносно прямої
![]() ,
якщо
координати його кінців знаходяться
відповідно в точках
,
якщо
координати його кінців знаходяться
відповідно в точках
![]() і
і
![]() .
.
Розв’язання:
Підставимо координати кінців відрізка в ліву частину рівняння даної прямої:
Для
точки
![]() :
:
![]() ;
;
Для
точки
:
![]() .
.
Точки і лежать в різних півплощинах відносно прямої, отже, відрізок перетинає дану пряму.
Відповідь:
відрізок
перетинає
пряму
![]()
Задача
2.
Записати рівняння прямої, яка проходить
через точки
![]()
Розв’язання:
Скористаємось
рівнянням прямої у вигляді:
.
Припускаючи, що в ньому,
![]() ,
отримаємо:
,
отримаємо:
![]()
Після
спрощень одержимо рівняння шуканої
прямої у вигляді:
![]()
Відповідь:
Задача
3.
Записати канонічне рівняння прямої,
яка проходить через точку
![]() і має напрямний вектор
і має напрямний вектор
![]() .
.
Розв’язання:
Скористаємося
рівнянням
![]() У нашому випадку
У нашому випадку
![]() .
Підставляючи ці значення в рівняння,
одержимо:
.
Підставляючи ці значення в рівняння,
одержимо:
![]() або
або
![]()
Відповідь:
Задача
4.
Загальне
рівняння прямої
![]() записати у вигляді рівняння прямої у
відрізках.
записати у вигляді рівняння прямої у
відрізках.
Розв’язання:
Нехай
точки
![]() і
і
![]() є відповідно точками перетину прямої
з координатними осями
і
. Для обчислення координат
є відповідно точками перетину прямої
з координатними осями
і
. Для обчислення координат
![]() і
і
![]() цих точок підставимо координати точок
у рівняння прямої.
цих точок підставимо координати точок
у рівняння прямої.
Маємо

Підставивши значення і в рівняння , отримаємо рівняння прямої у відрізках:

Відповідь:
Задача
5.
Загальне рівняння прямої
![]() записати в нормальному вигляді.
записати в нормальному вигляді.
Розв’язання:
Щоб
привести загальне рівняння прямої до
нормального вигляду, обидві частини
слід помножити на нормуючий множник
![]() .
Знак нормуючого множника береться
протилежним знаку вільного члена в
загальному рівнянні прямої. У нашому
випадку вільний член дорівнює
.
Знак нормуючого множника береться
протилежним знаку вільного члена в
загальному рівнянні прямої. У нашому
випадку вільний член дорівнює
![]() ,
отже нормуючий множник беремо зі знаком
«+». Далі
,
отже нормуючий множник беремо зі знаком
«+». Далі
![]()
Помноживши обидві частини рівняння на , приводимо його до нормального вигляду й отримаємо:
![]() або
або
![]()
Зауваження. Необхідно запам’ятати, що в нормальному рівнянні прямої сума квадратів коефіцієнтів при плинних координатах повинна дорівнювати одиниці, а вільний член має бути від’ємним.
Задача
6.
Визначити площу
![]() і периметр
і периметр
![]() трикутника, який знаходиться між осями
координат і прямою
трикутника, який знаходиться між осями
координат і прямою
![]() .
.
Розв’язання:
Загальне рівняння прямої перетворимо в рівняння прямої у відрізках:
![]()
Пряма відтинає на осях координат відрізки довжиною в 4 і 3 одиниці, отже,
![]()
Для
знаходження периметра трикутника
знайдемо довжину
![]() його гіпотенузи. Гіпотенуза визначена
точками
його гіпотенузи. Гіпотенуза визначена
точками
![]() і
і
![]() .
.
Тоді
![]()
![]()
Відповідь:
![]() ,
,
![]() .
.
Задача
7.
Обчислити відстань від точки
![]() до прямої
до прямої
![]() .
.
Розв’язання:
Згідно з наведеним правилом приведемо дане рівняння прямої до нормального вигляду. Обчислюємо нормуючий множник:
![]()
Нормальне
рівняння прямої запишеться так:
![]() .
.
Далі в
ліву частину цього рівняння
![]() підставимо координати даної точки.
Абсолютна величина одержаного числа і
дасть шукану відстань:
підставимо координати даної точки.
Абсолютна величина одержаного числа і
дасть шукану відстань:
![]()
Відповідь:
![]()
Задача 8. Написати рівняння прямої, яка паралельна бісектрисі другого координатного кута і яка відтинає на від’ємній піввісі відрізок, рівний 4.
Розв’язання:
Шукана
пряма, як і бісектриса другого координатного
кута, утворює з віссю
кут, рівний
![]() ,
тому її кутовий коефіцієнт
,
тому її кутовий коефіцієнт
![]() .
.
Крім
того, відомо, що
![]() .
Тоді можна записати рівняння шуканої
прямої у вигляді:
.
Тоді можна записати рівняння шуканої
прямої у вигляді:
![]() .
.
Відповідь:
![]() .
.
Задача 9. Обчислити кут між прямими:
![]() ;
;
![]()
Розв’язання:
У нашому
випадку
![]() за формулою:
за формулою:
![]() маємо:
маємо:
![]()
![]()
Отже,
кут між прямими
![]()
Відповідь:
кут між прямими
![]()
Задача 10. Визначити взаємне розміщення прямих:
![]()
Розв’язання:
Дані прямі задано загальними рівняннями, отже:
![]() .
.
Перевіримо
виконання необхідної умови перпендикулярності
прямих:
![]() ,
маємо:
,
маємо:
![]() .
Отже, умова виконується, значить ці
прямі взаємно перпендикулярні.
.
Отже, умова виконується, значить ці
прямі взаємно перпендикулярні.
Відповідь: прямі взаємно перпендикулярні.
Задача
11.
Визначити взаємне розміщення прямих
![]() і
і
![]() .
.
Розв’язання:
Дані
прямі задано канонічними рівняннями,
отже,
![]()
![]()
![]() .
Перевіримо виконання умови паралельності
прямих
.
Перевіримо виконання умови паралельності
прямих
![]() ,
маємо:
,
маємо:
![]() .
Отже, умова виконується, значить дані
прямі паралельні або співпадають.
.
Отже, умова виконується, значить дані
прямі паралельні або співпадають.
Перевіримо,
чи співпадають прямі. Для цього перевіримо,
чи належить точка
![]() другій прямій.
другій прямій.
![]() .
Точка
.
Точка
![]() не належить другій прямій, отже, прямі
не співпадають. Вони паралельні.
не належить другій прямій, отже, прямі
не співпадають. Вони паралельні.
Відповідь: прямі паралельні.
Задача
12.
Знайти кут, утворений віссю
і прямою
![]() .
.
Розв’язання:
Задане
загальне рівняння прямої перепишемо у
вигляді рівняння з кутовим коефіцієнтом,
для чого розв’яжемо його відносно
змінної
![]() Кутовий коефіцієнт
Кутовий коефіцієнт
![]() ,
отже,
,
отже,
![]() і
і
![]()
Відповідь:
Задача
13.
Скласти рівняння прямої, яка проходить
через початок координат і точку
![]() .
.
Розв’язання:
Рівняння
прямої з кутовим коефіцієнтом має
вигляд:
![]() .
Згідно нашої умови маємо:
.
Згідно нашої умови маємо:
![]() .
Отже, рівняння прямої
.
Отже, рівняння прямої
![]()
Відповідь:
Задача 14. Знайти кут між прямими:
 і
і

 і
і
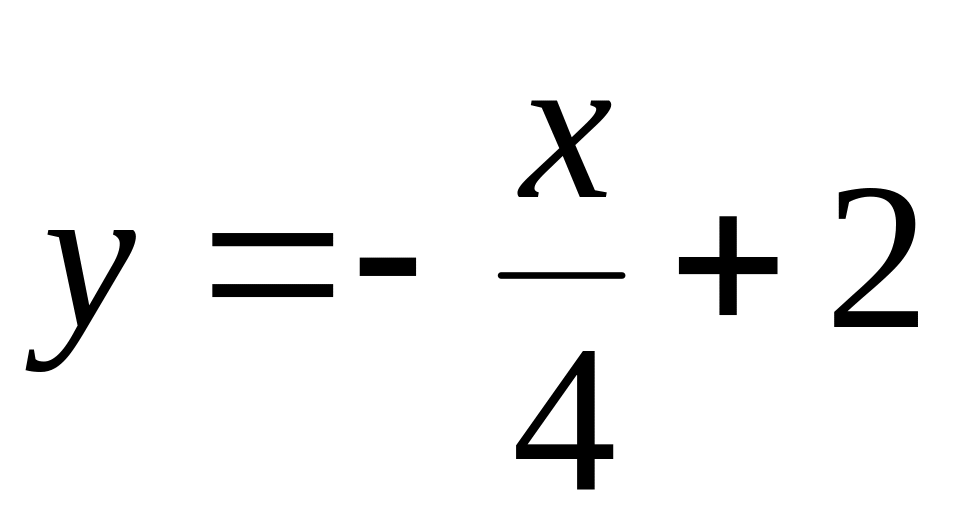 ;
;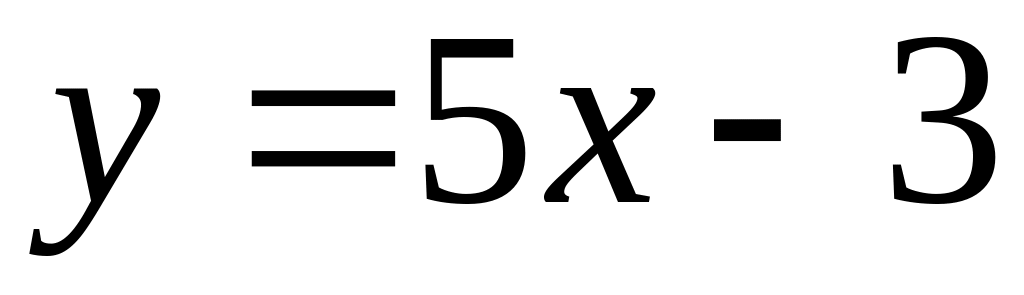 і
і
 .
.
Розв’язання:
 і
і
 звідки
звідки
 ;
; і
і
 - не існує, отже,
- не існує, отже,
 ;
;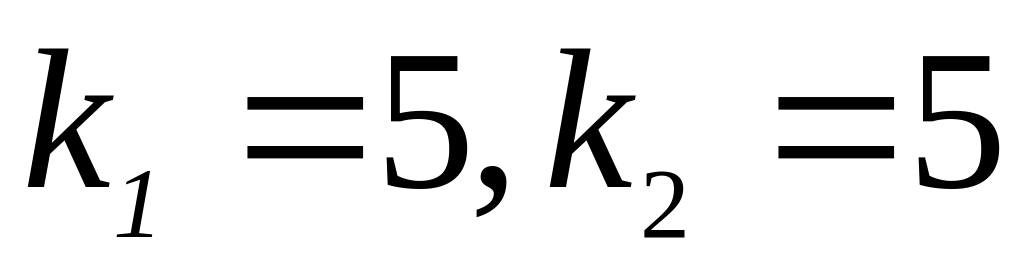 і
і
 ,
отже,
,
отже,
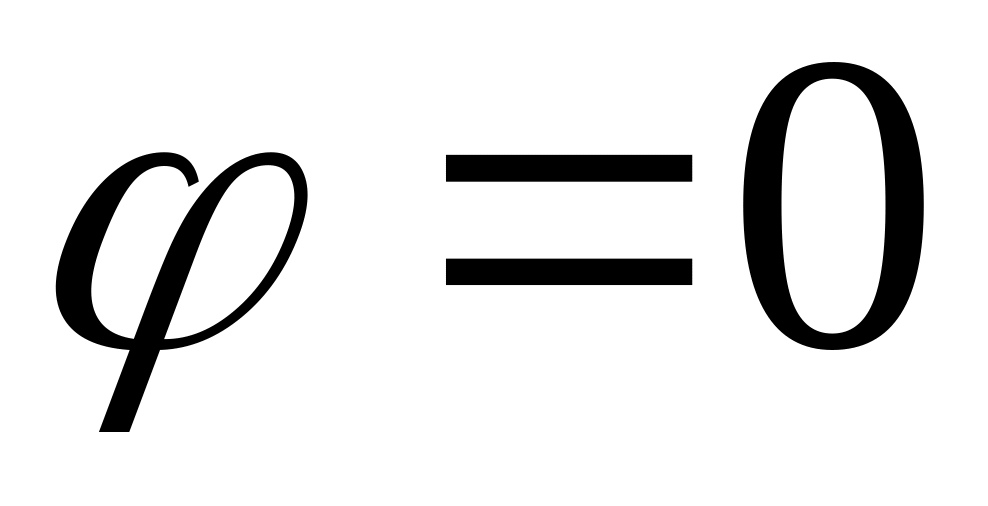 .
.
Відповідь: 1) ; 2) ; 3) .
Задача
15.
Скласти рівняння катетів рівнобедреного
прямокутного трикутника, знаючи рівняння
гіпотенузи
![]() і вершину прямого кута
і вершину прямого кута
![]() .
.
Розв’язання:
Так як трикутник прямокутний і рівнобедрений, то величина його гострих кутів дорівнює 45°.
Позначимо
![]() кутовий коефіцієнт прямої, на якій
лежить гіпотенуза, а
кутовий коефіцієнт прямої, на якій
лежить гіпотенуза, а
![]() кутовий коефіцієнт тієї прямої, на якій
лежить один з катетів трикутника, і яка
утворює з прямою, яка визначає гіпотенузу,
кут величиною 45°. Тоді тангенс кута між
цими прямими дорівнює 1.
кутовий коефіцієнт тієї прямої, на якій
лежить один з катетів трикутника, і яка
утворює з прямою, яка визначає гіпотенузу,
кут величиною 45°. Тоді тангенс кута між
цими прямими дорівнює 1.
Знайдемо
![]()
![]() звідки
звідки
![]() та
та
![]()
![]()
Знайдені
кутові коефіцієнти будуть визначати
рівняння двох катетів. Запишемо їх
рівняння: перший катет:
![]() або
або
![]() другий:
другий:
![]() ,
або
,
або
![]() .
.
Отже,
рівняння катетів:
![]() .
.
Відповідь: .
Задача 16. З’ясувати, які з перерахованих нижче пар прямих паралельні, співпадають або перетинаються (у випадку їх перетину знайти координати точки перетину):
 і
і
 ;
; і
і
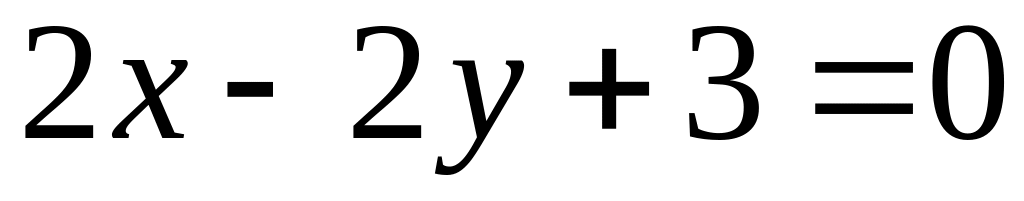 ;
; і
і
 .
.
Розв’язання:
Прямі задані своїми загальними рівняннями, тому необхідно порівняти відношення їх коефіцієнтів:
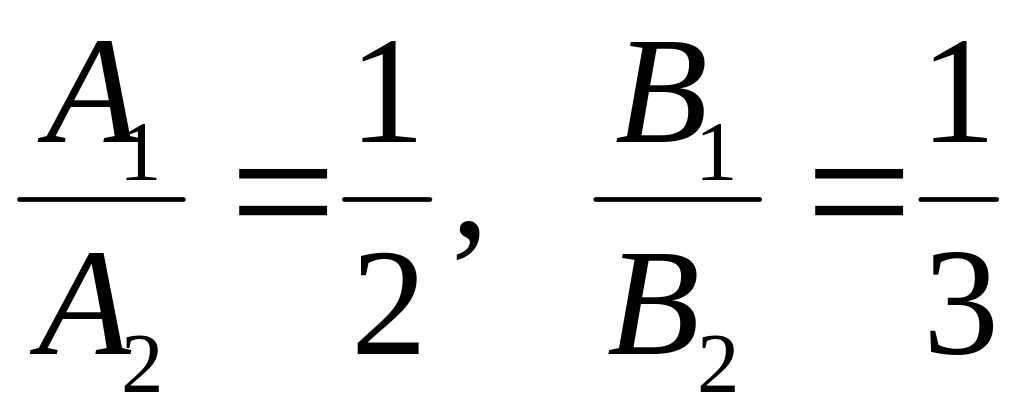 .
Так як
,
то прямі перетинаються.
.
Так як
,
то прямі перетинаються.
Для знаходження точки їх перетину розв’яжемо систему рівнянь
![]()
отримаємо
![]() .
.
Перетворимо рівняння другої прямої в рівняння з кутовим коефіцієнтом:
 У даних прямих рівні кутові коефіцієнти
У даних прямих рівні кутові коефіцієнти
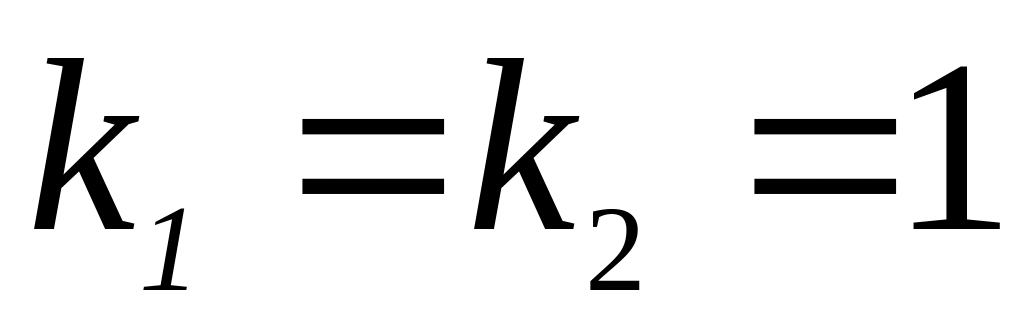 ,
а вільні члени не рівні
,
а вільні члени не рівні
 ,
отже, прямі паралельні.
,
отже, прямі паралельні.
Перетворимо друге рівняння в рівняння прямої з кутовим коефіцієнтом: . У даних прямих рівні кутові коефіцієнти
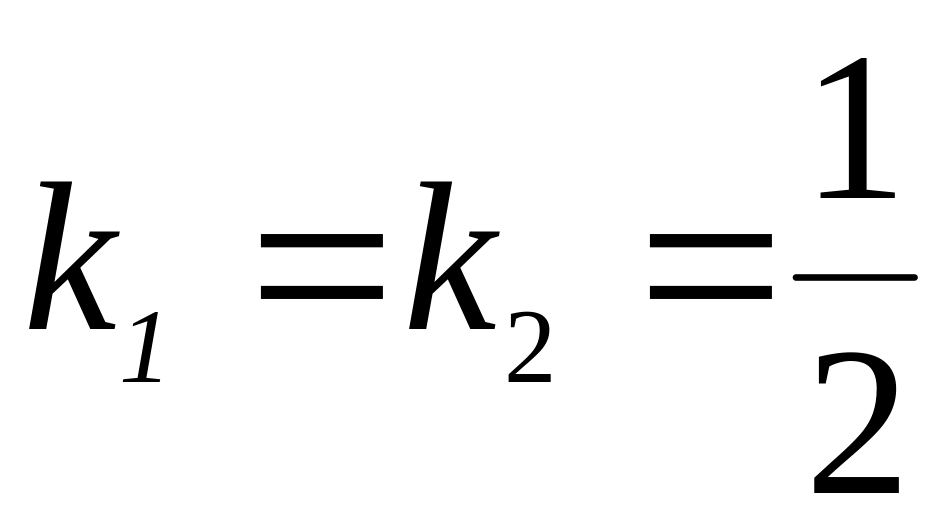 і вільні члени
і вільні члени
 ,
отже, прямі співпадають.
,
отже, прямі співпадають.
Можна
також перейти до загальних рівнянь
даних прямих:
![]() і
і переконатися в пропорційності
відповідних коефіцієнтів:
і
і переконатися в пропорційності
відповідних коефіцієнтів:
![]() .
.
Відповідь: 1) прямі перетинаються; 2) прямі паралельні; 3) прямі співпадають.
Задача
17.
Скласти рівняння прямої, яка проходить
через точку
![]() і паралельна прямій
і паралельна прямій
![]() .
.
Розв’язання:
Запишемо
загальне рівняння шуканої прямої
.
Так як шукана пряма паралельна даній,
то їх коефіцієнти при змінних
![]() і
і
![]() пропорційні, зокрема рівні. Тоді рівняння
шуканої прямої можна переписати у
вигляді
пропорційні, зокрема рівні. Тоді рівняння
шуканої прямої можна переписати у
вигляді
![]() .
Для знаходження коефіцієнта
.
Для знаходження коефіцієнта
![]() в рівняння прямої підставимо координати
точки
в рівняння прямої підставимо координати
точки
![]() ,
через яку проходить ця пряма:
,
через яку проходить ця пряма:
![]() .
.
Тоді
![]() є рівнянням шуканої прямої.
є рівнянням шуканої прямої.
Відповідь: .
Задача 18. Привести до нормального вигляду рівняння наступних прямих:
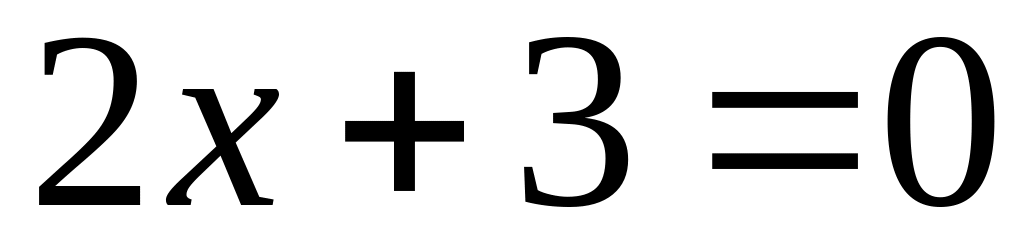 ;
; ;
; .
.
Розв’язання:
Знайдемо нормуючий множник:
 .
Так як
.
Так як
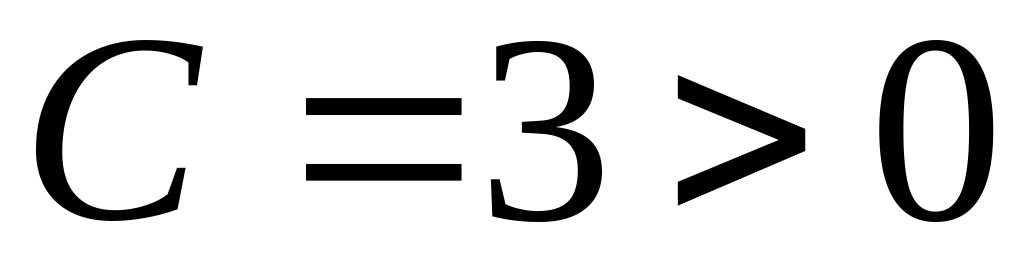 ,
то
,
то
 .
Помноживши обидві частини рівняння
на
.
Помноживши обидві частини рівняння
на
 одержимо:
одержимо:
 .
.Запишемо загальне рівняння даної прямої
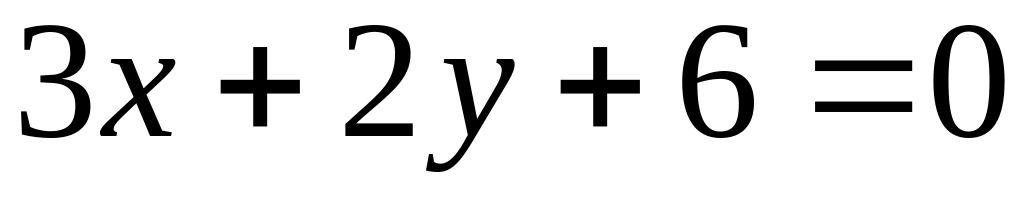 і помножимо обидві його частини на
нормуючий множник
і помножимо обидві його частини на
нормуючий множник
![]() так як
так як
![]()
![]()
Запишемо загальне рівняння даної прямої
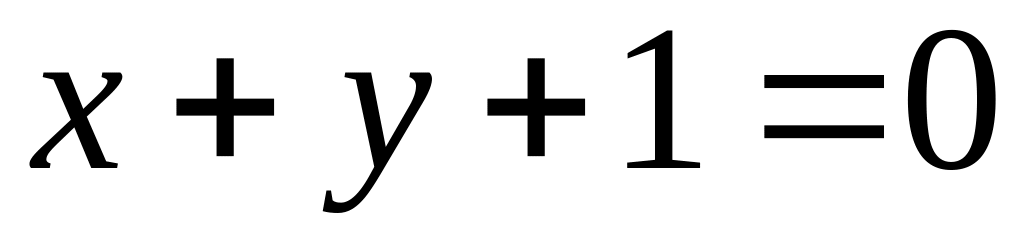 і помножимо обидві його частини на
нормуючий множник
і помножимо обидві його частини на
нормуючий множник
![]() так як
так як
![]()
![]()
Відповідь:
1)
;
2)
![]() ;
;
3)
Задача
19.
Знайти відстань від точки
![]() до прямої
до прямої
![]() .
.
Розв’язання:
Застосовуючи
формулу
![]() знайдемо шукану відстань:
знайдемо шукану відстань:
![]() .
.
Відповідь:
![]()
Задача
20.
Скласти рівняння прямих, паралельних
прямій
![]() і віддалених від неї на відстані, яка
дорівнює 5.
і віддалених від неї на відстані, яка
дорівнює 5.
Розв’язання:
Приведемо дане рівняння до нормального вигляду:
![]()
Якщо
точка
![]() – довільна точка шуканої прямої, то
вона віддалена від неї на відстань,
рівну 5, тобто повинна виконуватися
рівність:
– довільна точка шуканої прямої, то
вона віддалена від неї на відстань,
рівну 5, тобто повинна виконуватися
рівність:
![]()
Звідси одержуємо рівняння двох прямих, які задовольняють умові задачі:
![]() і
і
![]() ,
або
,
або
![]() і
і
![]()
Відповідь: , .
Задача
21.
Через точку
![]() провести дотичні до кола, яке має центр
в точці
провести дотичні до кола, яке має центр
в точці
![]() і радіус, рівний
і радіус, рівний
![]() .
.
Розв’язання:
Запишемо
рівняння всіх прямих, які проходять
через точку
:
![]() або
або
![]() Так як шукані прямі дотикаються до кола,
то вони віддалені від його центра на
відстань, рівну
.
Так як шукані прямі дотикаються до кола,
то вони віддалені від його центра на
відстань, рівну
.
Застосовуючи
формулу
![]() і підставляючи у неї координати точки
,
одержимо рівність
і підставляючи у неї координати точки
,
одержимо рівність
![]() з якої знайдемо
з якої знайдемо
![]() Підставляючи значення
Підставляючи значення
![]() в рівність
,
знайдемо шукані прямі:
в рівність
,
знайдемо шукані прямі:
![]() ,
або
,
або
![]() і
і
![]() .
.
Відповідь: , .
Задача
22.
Скласти рівняння бісектрис кутів між
прямими
![]() і
і
![]() .
.
Розв’язання:
Бісектриси
є геометричне місце точок, рівновіддалених
від сторін кута. Таким чином, якщо
–
довільна точка бісектриси, то її відстані
![]() і
і
![]() до двох даних прямих рівні між собою:
до двох даних прямих рівні між собою:
![]() Знайдемо ці відстані за формулою
Знайдемо ці відстані за формулою
![]()
![]()
![]() і скористаємось рівністю:
і скористаємось рівністю:
![]() або
або
![]()
Таким чином, одержимо рівняння бісектрис:
![]() або
або
![]() ,
,
і
![]() або
або
![]() .
.
Відповідь: , .
Задача
23.
Через точку перетину прямих
![]() і
і
![]() провести прямі, одна з яких проходить
через початок координат, а інша паралельна
осі абсцис.
провести прямі, одна з яких проходить
через початок координат, а інша паралельна
осі абсцис.
Розв’язання:
Запишемо
рівняння пучка, якому належать дані і
шукані прямі:
![]() .
.
Так як
перша шукана пряма проходить через
початок координат, то координати точки
![]() повинні задовольняти рівнянню пучка,
тобто
повинні задовольняти рівнянню пучка,
тобто
![]() .
Звідси
.
Звідси
![]()
Підставляючи
значення
![]() в рівняння пучка, одержимо:
в рівняння пучка, одержимо:
![]() або
або
![]() .
.
Для
знаходження рівняння другої прямої
рівняння пучка перепишемо в наступному
вигляді:
![]() ,
тобто у
вигляді загального рівняння прямої. В
рівнянні прямої, яка паралельна осі
абсцис, коефіцієнт при змінній
дорівнює 0, отже,
,
тобто у
вигляді загального рівняння прямої. В
рівнянні прямої, яка паралельна осі
абсцис, коефіцієнт при змінній
дорівнює 0, отже,
![]() ,
або
,
або
![]() .
Рівняння другої шуканої прямої:
.
Рівняння другої шуканої прямої:
![]() .
.
Відповідь: , .
З адача
24.
Визначити величину кута між гіпотенузою
адача
24.
Визначити величину кута між гіпотенузою
![]() і катетом
і катетом
![]() прямокутного трикутника.
прямокутного трикутника.
Розв’язання:
За умовою
відомо, що
![]() ,
тоді
,
тоді
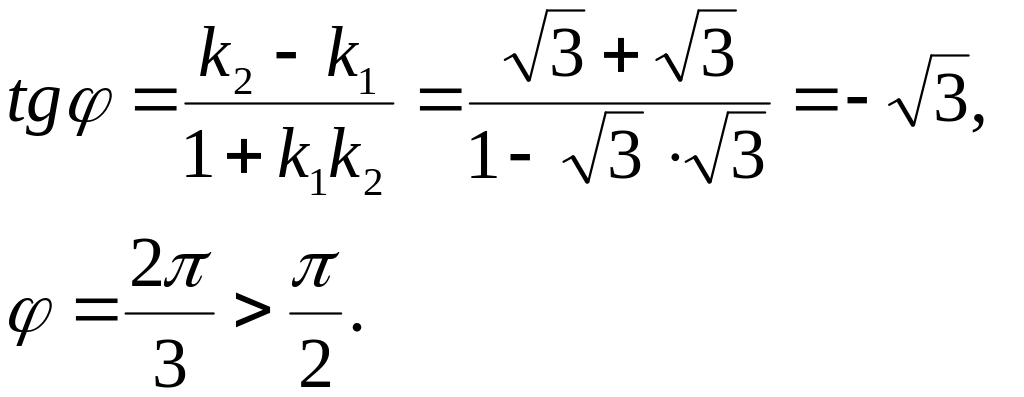
Так як
кут між гіпотенузою і катетом трикутника
гострий, то знайдена величина зовнішнього
кута трикутника, який суміжний з шуканим,
тому величина шуканого кута дорівнює
![]() .
.
Відповідь:
![]() .
.
Задача
25.
Через точку перетину прямих
![]() ,
,
![]() провести пряму, паралельну прямій
провести пряму, паралельну прямій
![]() .
.
Розв’язання:
Запишемо рівняння пучка прямих, який утворюють дані прямі:
![]() ,
або
,
або
![]() .
.
Шукана
пряма паралельна даній, отже, повинне
виконуватися співвідношення
![]() ,
звідки
,
звідки
![]() .
.
Підставляючи
в рівняння пучка, одержимо рівняння
шуканої прямої:
![]() .
.
Відповідь: .
Задача 26. З’ясувати, які з наведених пар прямих взаємно перпендикулярні:
 і
і
 ;
;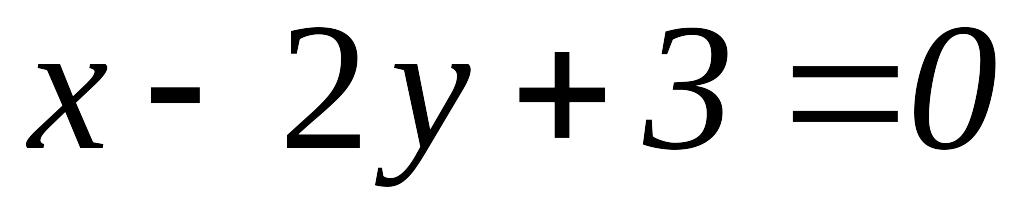 і
і
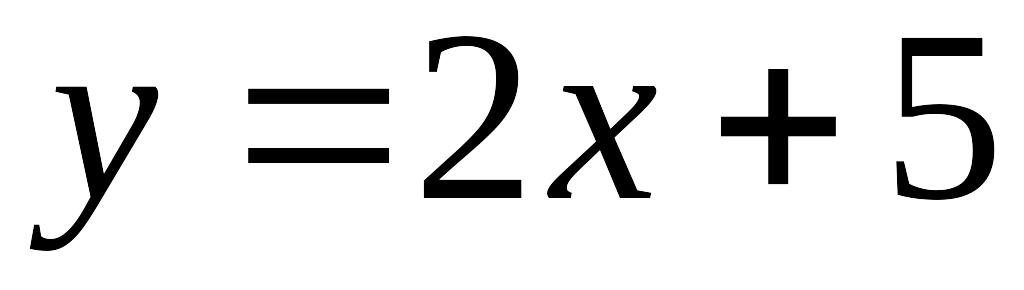 ;
;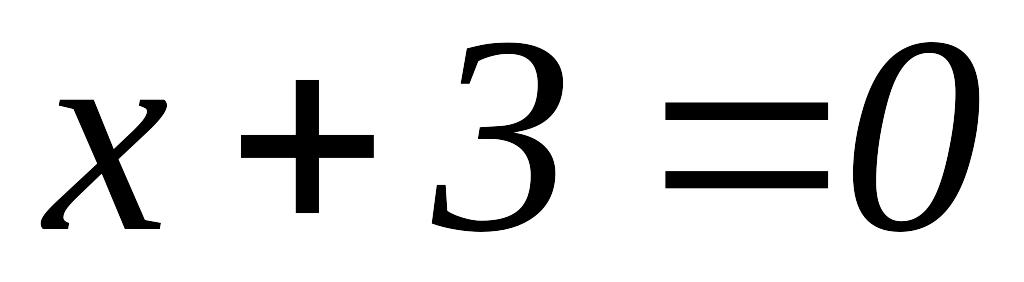 і
і
 ;
; і
і
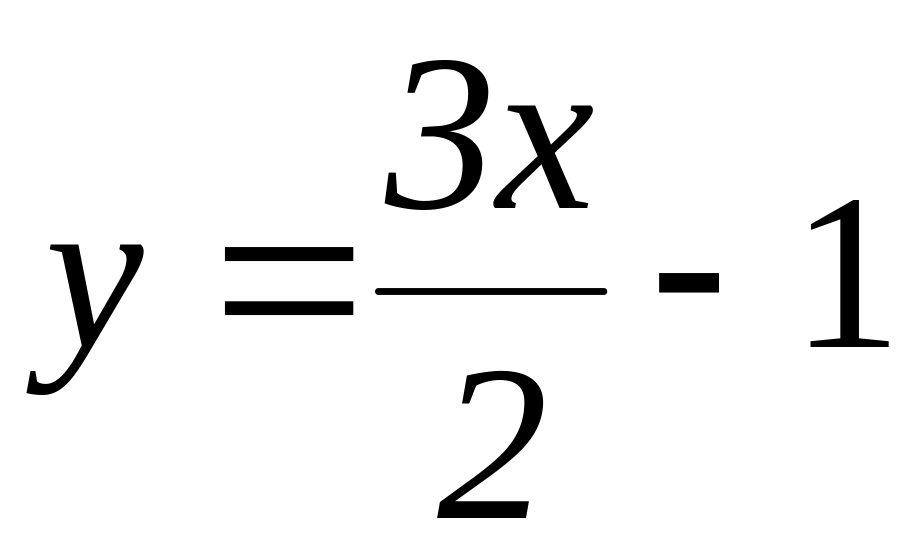 .
.
Розв’язання:
Прямі задані загальними рівняннями. Перевіримо для них виконання умови перпендикулярності
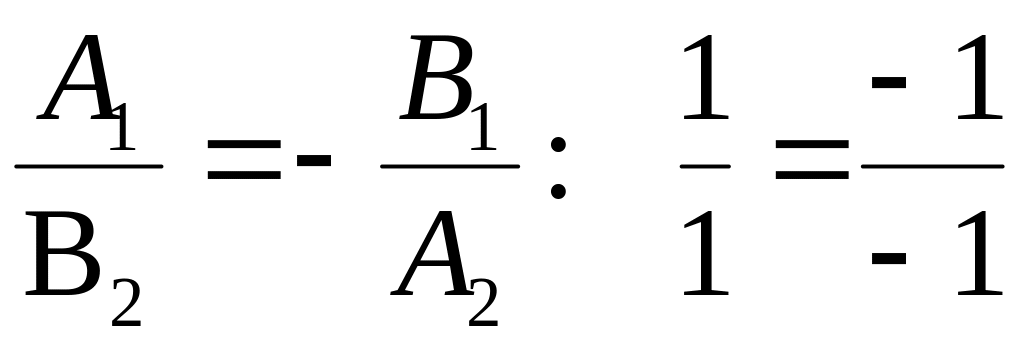 .
Прямі перпендикулярні.
.
Прямі перпендикулярні.Перше рівняння перетворимо в рівняння прямої з кутовим коефіцієнтом:
![]() .
Перевіримо виконання умови
.
Перевіримо виконання умови
 перпендикулярності двох прямих, які
задані рівнянням з кутовим коефіцієнтом:
перпендикулярності двох прямих, які
задані рівнянням з кутовим коефіцієнтом:
![]() .
Прямі не перпендикулярні.
.
Прямі не перпендикулярні.
Прямі перпендикулярні, тому що одна з них паралельна осі ординат, інша – осі абсцис.
Перше рівняння перетворимо в рівняння прямої з кутовим коефіцієнтом:
 .
Так як
.
Так як
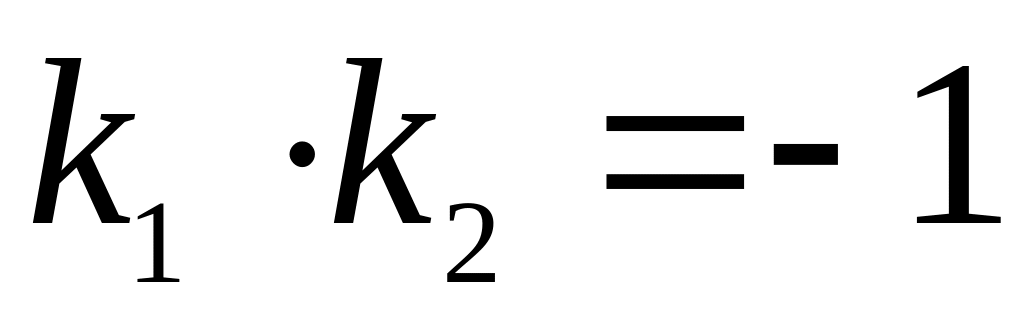 ,
то дані прямі перпендикулярні.
,
то дані прямі перпендикулярні.
Відповідь: 1) прямі перпендикулярні; 2) прямі не перпендикулярні; 3) прямі перпендикулярні; 4) прямі перпендикулярні.
Задача
27.
Знайти рівняння перпендикуляра, який
проведено через точку перетину прямих
![]() і
і
![]() до першої прямої.
до першої прямої.
Розв’язання 1:
Розв’язуючи систему рівнянь
![]()
знайдемо
точку
перетину прямих:
![]() .
.
Знайдемо
кутовий коефіцієнт
![]() першої даної прямої:
першої даної прямої:
![]() Так як шукана пряма перпендикулярна
першій з даних прямих, то її кутовий
коефіцієнт
Так як шукана пряма перпендикулярна
першій з даних прямих, то її кутовий
коефіцієнт
![]() .
Знаючи кутовий коефіцієнт і точку, яка
належить прямій, запишемо її рівняння:
.
Знаючи кутовий коефіцієнт і точку, яка
належить прямій, запишемо її рівняння:
![]() ,
або
,
або
![]() .
.
Розв’язання2:
Запишемо рівняння пучка прямих, визначеного заданими прямими:
![]() .
.
Виразимо через кутовий коефіцієнт шуканої прямої:
![]() ,
і скористаємося умовою
перпендикулярності шуканої і першої з
даних прямих, знаючи, що кутовий коефіцієнт
першої даної прямої
,
і скористаємося умовою
перпендикулярності шуканої і першої з
даних прямих, знаючи, що кутовий коефіцієнт
першої даної прямої
![]() ,
звідки
,
звідки
![]() .
Підставляючи значення
в рівняння пучка, знайдемо рівняння
шуканої прямої:
.
.
Підставляючи значення
в рівняння пучка, знайдемо рівняння
шуканої прямої:
.
Відповідь: .
Задача
28.
Знайти точку, симетричну точці
![]() відносно прямої
відносно прямої
![]() .
.
Розв’язання:
Якщо
![]() – точка, симетрична точці
відносно прямої
,
то точки
і
лежать на прямій
– точка, симетрична точці
відносно прямої
,
то точки
і
лежать на прямій
![]() ,
яка перпендикулярна прямій
і рівновіддалені від цієї прямої, тобто
,
яка перпендикулярна прямій
і рівновіддалені від цієї прямої, тобто
![]() ,
де
,
де
![]() – проекція точки
на дану пряму. Знайдемо рівняння прямої
.
– проекція точки
на дану пряму. Знайдемо рівняння прямої
.
Т
M



![]()
![]() ,
то кутовий коефіцієнт прямої
,
то кутовий коефіцієнт прямої
N![]()


![]() ,
буде таким:
,
буде таким:
![]() ,
або
,
або
![]() .
.
Знайдемо
координати точки
,
як точки перетину даної прямої і прямої
.
Для цього розв’яжемо систему:
![]() .
Точка
.
Точка
![]() ділить навпіл відрізок
.
Із співвідношень
ділить навпіл відрізок
.
Із співвідношень
![]() і
і
![]() знайдемо координати
і
шуканої точки
знайдемо координати
і
шуканої точки
![]()
![]()
![]()
![]()
Відповідь:
точка
![]() .
.
Задача
29.
3найдіть відстань між паралельним
прямими
![]() і
і
![]() .
.
Розв’язання1:
Скористаємось
формулою
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
Розв’язання2:
Візьмемо
на першій прямій довільну точку,
наприклад, точку
![]() ,
і за формулою
,
і за формулою
![]() знайдемо відстань
знайдемо відстань
![]() від неї до другої прямої:
від неї до другої прямої:
![]() Ця відстань і є відстанню між даними
прямими.
Ця відстань і є відстанню між даними
прямими.
Відповідь:
![]() .
.
