Дифференциальное уравнение массоотдачи (конвективной диффузии)

Распределяемое вещество переносится из ядра потока жидкости к границе раздела фаз непо-средственно потоками жидкости и молекуляр-ной диффузией.

В ядре перенос вещества осуществляется преи-мущественно токами жидкости и в условиях до-статочной торбулентности течения; концентра-ция распределяемого вещества в данном сече-нии в условиях стационарного режима сохраня-ется постоянной.

Распределяемое вещество переносится из ядра потока жидкости к границе раздела фаз непо-средственно потоками жидкости и молекуляр-ной диффузией.

В ядре перенос вещества осуществляется преи-мущественно токами жидкости и в условиях до-статочной торбулентности течения; концентра-ция распределяемого вещества в данном сече-нии в условиях стационарного режима сохраня-ется постоянной.

Перенос массы распределяемого вещества вследствие молекулярной диффу-зии математически описывается дифференциальным уравнением молекуляр-ной диффузии (14)

локальное изменение концентрации распределяемого вещества в неподвижном элементе, выделенном в среде

При конвективной диффузии элемент перемещается из одной точки про-странства в другую. При этом изменение концентрации распределяемого ве-щества в элементе может быть выражено при помощи субстанциальной про-изводной, учитывающей изменение величины во времени и изменения, свя-занные с перемещением элемента из одной точки пространства в другую:

(17) локальное изменение концентрации конвективное изменение концентрации

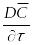
Дифференциальное уравнение конвективной диффузии

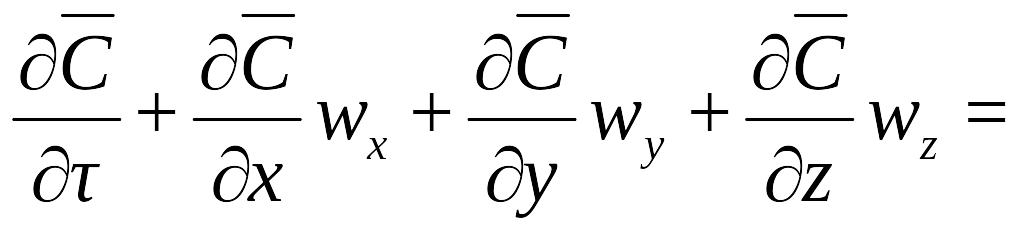
Массопроводность

Это процесс распределения компонента в системе твердое тело – жидкость (адсорбция, сушка, выщелачи-вание). Процесс характеризуется более медленным протеканием по сравнению с массоотдачей. Это объясняется стесненными условиями.

Количество вещества, переместившегося в твердой фазе за счет массопроводности, пропорционально градиенту концентрации, площади, перпендикулярной направлению потока вещества, и времени, т.е.

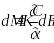(19)

где К — коэффициент массопроводности.

Массопередача

Основное уравнение массопередачи:M = KΔСF,

где М — масса переданного в единицу времени вещества из одной фазы в другую, кг/с;

К — коэффициент массопередачи кг/(м²·с); ΔС — движущая сила процесса, кг/кг;

F — площадь контакта фаз, м².

Количество распределяемого вещества, перемеща-ющегося из фазы G к элементу поверхности на границе раздела фаз может быть вычислено по уравнению (15) , выражая движущую силу через разность x – x_p:

dM = β_x(x – x_p)dF

То же количество распределяемого вещества, перемещающегося от элемента поверхности на границе раздела фаз в фазу L, может быть вычислено аналогично, выражая движущую силу через раз-ность у_p – у:

dM = β_у(у_p – у)dF

где β_x, β_у— коэффициенты массоотдачи в соответствующих фазах.

Коэффициент массопередачи может быть выражен через частные коэффициенты массоотдачи, характеризующие скорость процесса массообмена в каждой фазе:

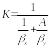— коэффициент массопередачи

где А — характеризует угол наклона рабочей линии y = Ax + B.