2.3. Инерционные модели

Динамические системы с последействием (с предысторией) могут быть формализованы с применением дифференциальных уравнений с запаздывающим аргументом.

2.3.1. Дифференциальные уравнения с запаздывающими аргументами. В общем случае дифференциальные уравнения n-го порядка с запаздывающим аргументом имеют вид

. (2.14)

Дифференциальное уравнение (2.14) может быть сведено к системе дифференциальных уравнений первого порядка. Введем обозначения: z=z₁; ; и т.д. Тогда дифференциальное уравнение (2.14) запишем в следующем виде:

.

Из рассмотрения даже простейшего дифференциального уравнения вида

, (2.15)

где >0, =сonst, сложно понять, какие начальные условия надо задать, чтобы определить решение z(t) для t>t₀.

Решение дифференциального уравнения (2.15) определяется из интегрального уравнения

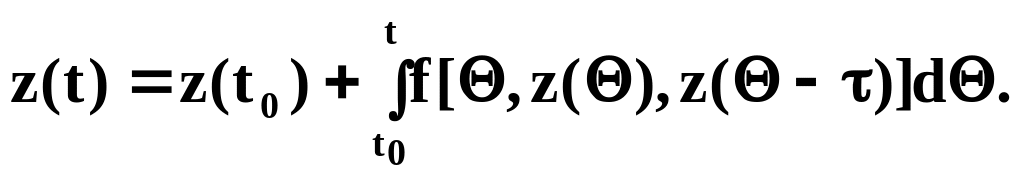(2.16)

Решение уравнения (2.16) осуществляется по следующему алгоритму.

Следует задать начальное значение для точки t₀ z₀=z(t₀) и функцию z(t) в полуинтервале t₀-t<t₀ ([t₀-, t₀)). Функцию z(t)=W(t) называют начальной функцией t[t₀-,t₀). При таких условиях можно получить либо аналитическое решение уравнения (2.16), либо получить решение для любого >t₀ с применением методов вычислительной математике и компьютерного моделирования. Алгоритм решения уравнения (2.16) представляет собой следующую последовательность действий.

После задания начальных условий следует определить непрерывное решение z(t) для t>t₀, при условии, что z(t)=W(t) для t[t₀-,t₀). Если функции f и W непрерывны и первая из них удовлетворяет условию Липшица по z, то искомое решение существует и единственно.

Зная W(t) для t₀-t<t₀, найдем z(t) для t₀t<t₀+. Примем это z(t) за начальную функцию W(t) для t₀t<t₀+. Определим z(t) для t₀+t<t₀+2 и т.д.

При поиске решения применен метод последовательного интегрирования, сущность которого показана на рис. 2.3.

Дифференциальные уравнения с запаздывающим аргументом применяются для составления моделей динамической системы с последствием, т.е. систем, для определения состояний z(t) которых при t>t₀ недостаточно задать z₀=z(t₀).

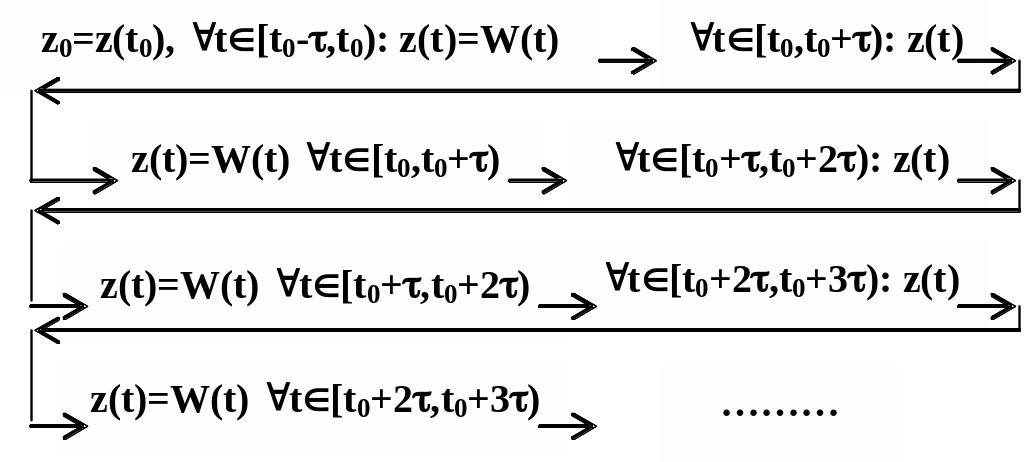
Рис. 2.3

2.3.2. Модели в виде сумм и интегралов свертки. Если динамическая система функционирует в дискретные моменты времени, то ее модель может быть описана в виде суммы свертки. Математические модели, выражаемые суммой свертки или интеграла свертки, задаются следующим образом. Для однооткликовой стационарной динамической системы, на вход которой действует управляющая функция х(t), а наблюдения над входом и выходом производятся только в дискретные моменты времени с интервалом квантования t, математическая модель может быть выражена с помощью суммы свертки:

Зададим масштаб t=1, получим

(2.17)

Модель (2.17) является моделью импульсной системы, h(i) есть импульсная характеристика системы, представляющая собой отклик системы в данный момент времени на входное воздействие, приложенное на i интервалов раньше и имевшее характер единичного мгновенного импульса в виде функции Дирака. Импульсная характеристика играет здесь роль весовой функции.

Если линейная динамическая система нестационарная, то в выражения (2.17) нельзя применять импульсную характеристику системы вида h(k-i). Для этого случая математическая модель примет вид

где h(k,i) - реакция системы в момент k на единичный импульс в момент i.

В модели типа суммы свертки роль величин, подлежащих определению из экспериментальных данных, играют значения импульсной характеристики, т.к. данная модель является непараметрической, т.е. не содержит явно параметров в виде некоторых численных величин. Если в динамической системе измерения управляющей функции и отклика носят непрерывный характер, то модель линейной системы может быть записана в виде интеграла свертки:

- для линейной системы

; (2.18)

- для нестационарной системы

Модель представлена в виде функционала с аддитивной ошибкой v(t). Интеграл называется интегралом свертки, или интегралом Дюамеля. Для определения импульсной характеристики (весовой функции) используется (для стационарных систем) представление весовой функции в форме Релея-Ритца путем разложения функций в ряд по системе известных ортогональных функций

(2.19)

где Ф_i(t) - функции системы ортогональных функций при значениях t, принадлежащих отрезку ортогональности [t₁,t₂]. Это позволяет сделать модель параметрической, которая содержит ограниченное число параметров _i, подлежащих определению. Коэффициенты _i называют еще спектром разложения в ряд базисных функций.

К системе базисных функций предъявляются следующие требования: для любой весовой функции ряд (2.19) должен сходиться; Ф_i(t) должна иметь простую аналитическую форму; _i должны вычисляться аналитически просто.

Условие ортогональности базисных функций имеет вид

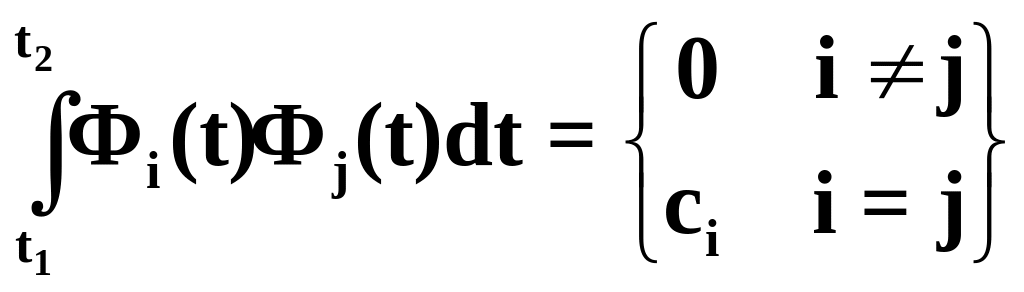, (2.20)

где число с_i называют нормой базисной функции Ф_i(t).

Каждую базисную функцию можно нормировать по ее норме, причем нормированная функция имеет вид

.

Система (2.20) примет вид

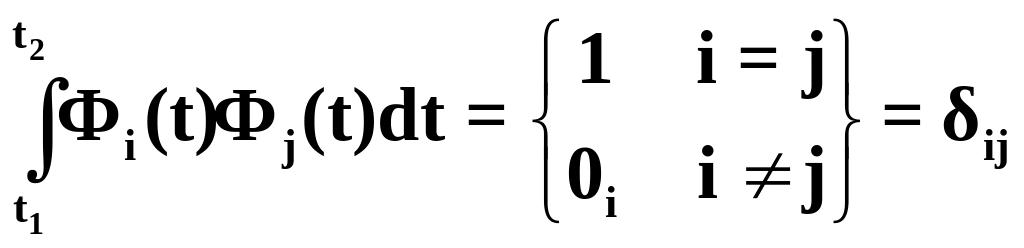, (2.21)

где _ij - символ Кронекера.

Для определения _i умножим правую и левую части уравнения (2.19) на Ф_i(t) и проинтегрируем обе части на отрезке ортогональности

.

При k=i правый интеграл равен единице, тогда

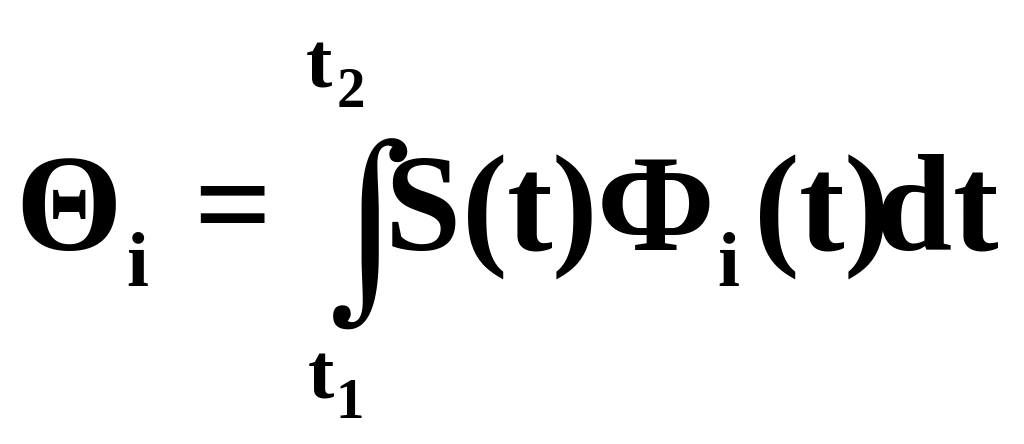. (2.22)

Модели вида свертки могут использоваться и для описания многооткликовых линейных инерционных систем.