6.2. Табличное задание функций переходов и выходов

Задание условных вероятностных мер Р(z_t,y_t/z_t-1,х_t) возможно как задание стохастического отображения ZХZY табличным способом. В табл. 6.1 приведен вид совместного задания функций переходов и выходов.

Таблица 6.1

Совместное задание функций переходов и выходов

ZХ	ZY
	z1y1	z1y2	…	z1yr	…	zny1	zny2	…	znyr
z1х1			…		…			…
…	…	…	…	…	…	…	…	…	…
z1хm			…		…			…
…	…	…	…	…	…	…	…	…
znх1			…		…			…
…	…	…	…	…	…	…	…	…	…
znхm			…		…			…

Элементы каждой строки табл. 6.1 должны быть нормированы, т.е.

.

Функция переходов может быть представлена как стохастическое отображение элементов множества ZХ в элементы множества Z. В табл. 6.2 приведен общий вид задания функции переходов. Элементы каждой строки табл. 6.2 также отвечают условию нормирования, т.е.

Таблица 6.2

Задание функции переходов

ZХ	Z
	z1	z2	…	zn
z1х1			…
…	…	…	…	…
z1хm			…
…	…	…	…	…
znх1			…
…	…	…	…	…
znхm			…

Функция выходов может быть представлена как стохастическое отображение элементов множества ZХZ в элементы множества Y.

В табл. 6.3 приведен общий вид задания функции выходов. Элементы каждой строки табл. 6.3 отвечают условию нормирования, т.е.

.

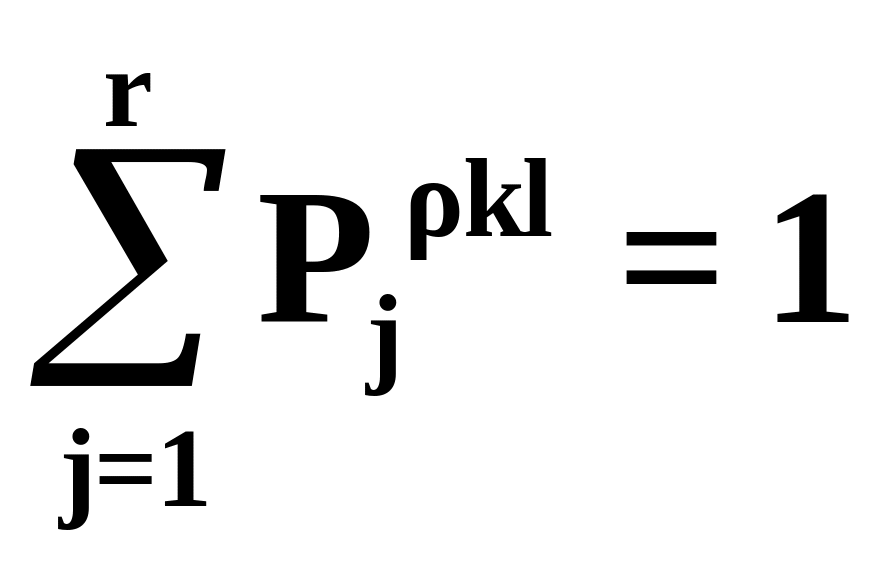Таблица 6.3

Задание функции выходов

ZХZ	Y
	y1	y2	…	yn
z1х1z1			…
…	…	…	…	…
znх1zn			…
…	…	…	…	…
znхmz1			…
…	…	…	…	…
znхmzn			…

При применении аппарата вероятностных автоматов для решения задач моделирования сложных систем необходимо определить множества входных параметров, состояний и выходных параметров, определить функции переходов и выходов. Следующим этапом в моделировании будет идентификация значений вероятностей функций переходов и выходов и проверка адекватности найденной модели.