5.3. Формулы и алгоритмы для оценки результатов моделирования

При реализации моделирующего алгоритма на ЭВМ вырабатывается информация о состоянии моделируемых систем, которая представляет собой исходный материал для определения приближенных искомых величин по статистическим данным. Желательно так организовать фиксацию и алгоритмы обработки результатов моделирования, чтобы статистические оценки для искомых величин формировались постепенно по ходу моделирования, без специального запоминания всей информации о состояниях системы [8].

Если при моделировании учитываются случайные факторы, то в качестве оценок для искомых величин используются средние значения, дисперсия и другие вероятностные характеристики. В памяти ЭВМ для формирования оценки желательно занимать как можно меньше ячеек. При моделировании случайных событий оценка Р(A) вероятности Р(A) события A определится по формуле

Р*(A)=m/N, (5.22)

где m — число случаев (частота) наступления событий A, N - число реализаций (объем выборки). В данном случае для подсчета частоты достаточно предусмотреть один счетчик К, содержимое которого будет увеличиваться на единицу каждый раз при наступлении события A. Для получения значения Р*(A) после окончания моделирования содержимое счетчика К делится на N.

Если событие принимает значения в некоторой области величин, то область значений n случайной величины разбивается на отрезки так, что n={n₁,n₂…n_m}, . Оценка вероятностей возможных i-х значений случайной величины определяется

Р*_i(A)=m_i/N, (5.23)

где m_i - число значений случайной величины в интервале n_i. Для подсчета частоты необходимо предусмотреть m счетчиков К[I], содержимое которых будет увеличиваться на единицу каждый раз тогда, когда случайное событие A принимает значение из интервала n_i.

Для получения значения Р*_i(A) после окончания моделирования содержимое i-го счетчика К[I] делится на N. Алгоритм приведен на рис. 5.5. Примером непрерывной случайной величины A могут быть интервалы времени между движущимися автомобилями.

Если задать границы D(J), , где JМ - заданное число границ оценки этой случайной величины А, то можно определить частоты событий А(J), состоящие в том, что значения случайной величины A меньше или равны границам D(J). Частоты А(J) записаны в счетчиках К(J), .

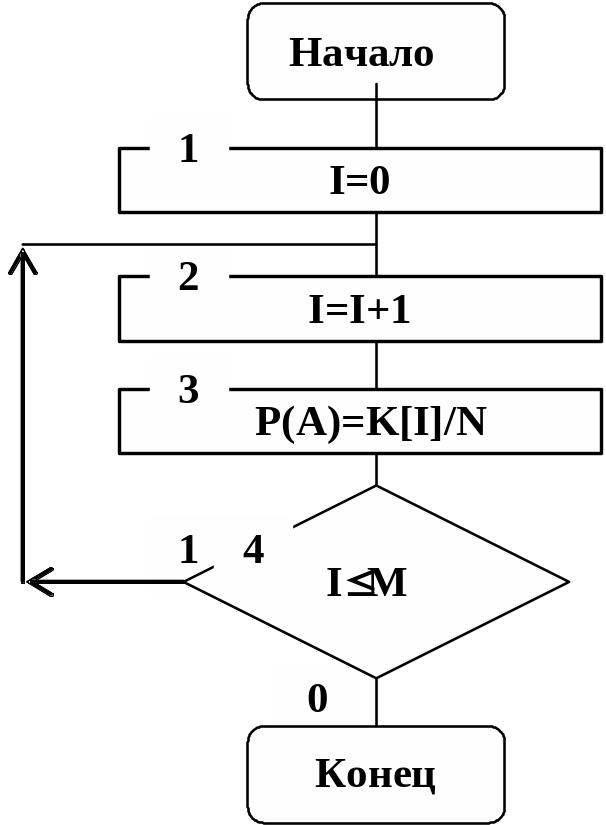
Рис. 5.5

Величина D(JМ) является наибольшей границей оценки случайной величины, т.е. D(1)<D(2)<…<D(JМ). Частота К(J) события А определена тем, что значение события меньше либо равно границе D(J).

На рис 5.6 приведен алгоритм подпрограммы STAT набора статистических данных. Входной переменной подпрограммы STAT является значение X непрерывной случайной величины A. В блоках 1, 2, 5 реализован цикл по переменной J. В блоке 3 проверяется условие, что значения X случайной величины A меньше или равны границам D(J). Если условие выполняется, то содержимое соответствующего счетчика К(J) увеличивается на единицу (см. блок 4).

В табл. 5.1 приведен пример частот некоторой случайной величины А. Обработка статистических данных, приведенных в табл. 5.1, позволяет построить кумулятивную эмпирическую функцию распределения.

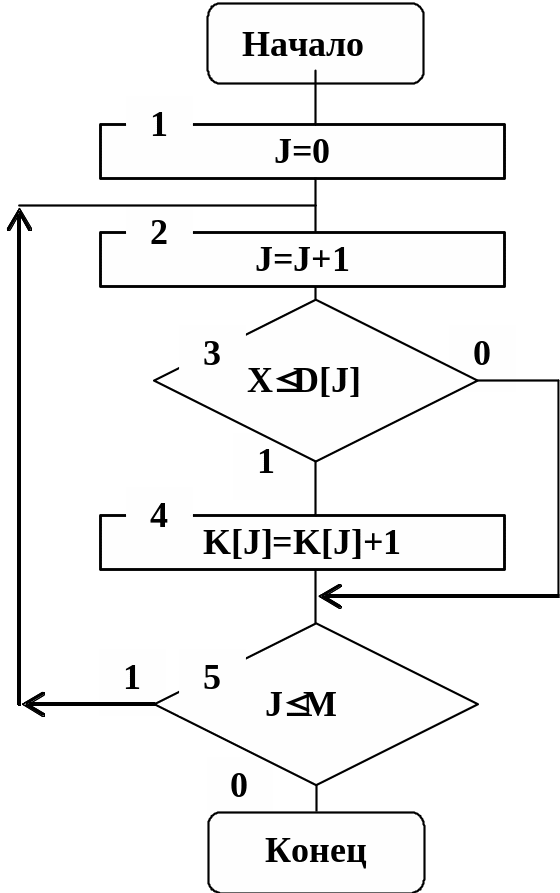
Рис. 5.6

Таблица 5.1

Статистические данные результатов моделирования

Границы оценки	D(1) 2	D(2) 4	D(3) 6	D(4) 8	D(5) 10	D(6) 15	D(7) 20	D(8) 25
Номер счетчика	К(1)	К(2)	К(3)	К(4)	К(5)	К(6)	К(7)	К(8)
Частота события	37	100	193	240	280	362	425	500

Определяются частости появления события А в соответствии с формулами:

где P_j - теоретическое значение вероятностей.

Затем строится гистограмма кумулятивной эмпирической функции распределения по значениям P_j^*. Пример построения приведен на рис. 5.7.

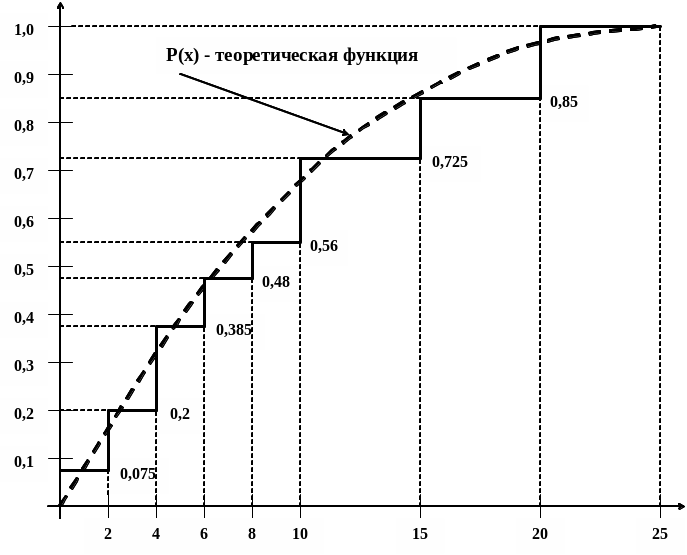
Рис. 5.7

Выдвигается гипотеза, состоящая в том, что найденная кумулятивная эмпирическая функция распределения может быть аппроксимирована известным теоретическим распределением P(x) (см. рис. 5.7). Проверка гипотезы осуществляется по критерию ² (см. разд. 5.2.3).

Если определять частоты событий А(J), состоящие в том, что значения случайной величины A принадлежит интервалу (D(J+1)-D(J)), , и эти частоты записывать в счетчики К(J), , то алгоритм подпрограммы STAT в этом случае будет иметь вид, приведенный на рис. 5.8.

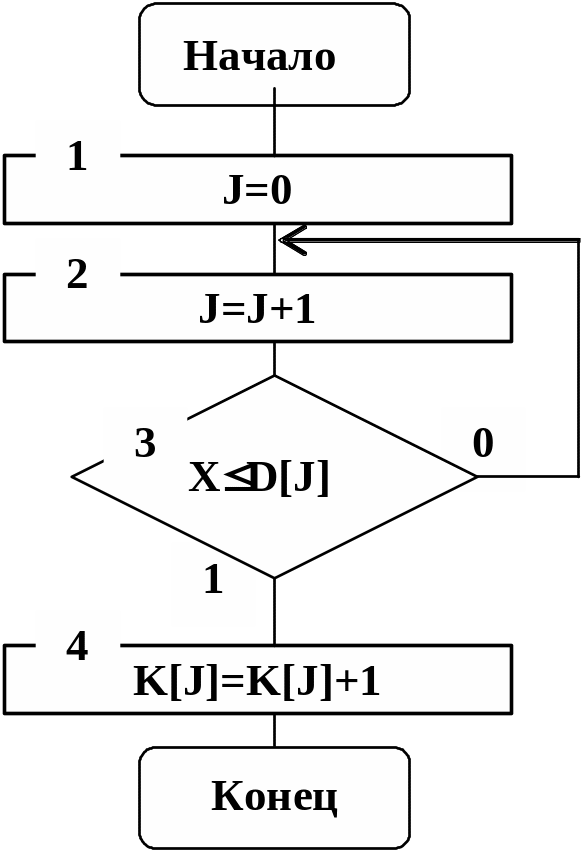
Рис. 5.8

Можно получить по статистическим данным - частости попадания случайной величины A в интервалы (D(J+1)-D(J)), :

; ; ; …; .

Затем определить отношение к величине j-го интервала (D(J+1)-D(J)):

Если при моделировании в счетчиках К(J) будут получены частоты событий, состоящих в том, что случайная величина А принадлежит интервалу (D(J+1)-D(J)), то частости определятся:

Для построения кумулятивной эмпирической функции распределения частости определятся следующим образом:

Среднее значение случайной величины определяется по формуле

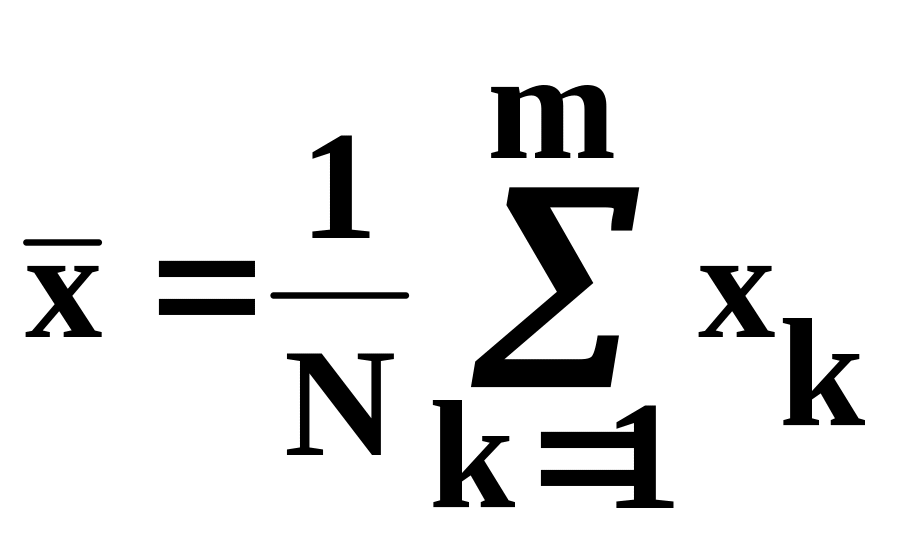, (5.24)

где х_k - возможные значения случайной величины, которые она принимает при различных реализациях процесса. На рис. 5.9 приведен алгоритм для определения среднего значения случайной величины.

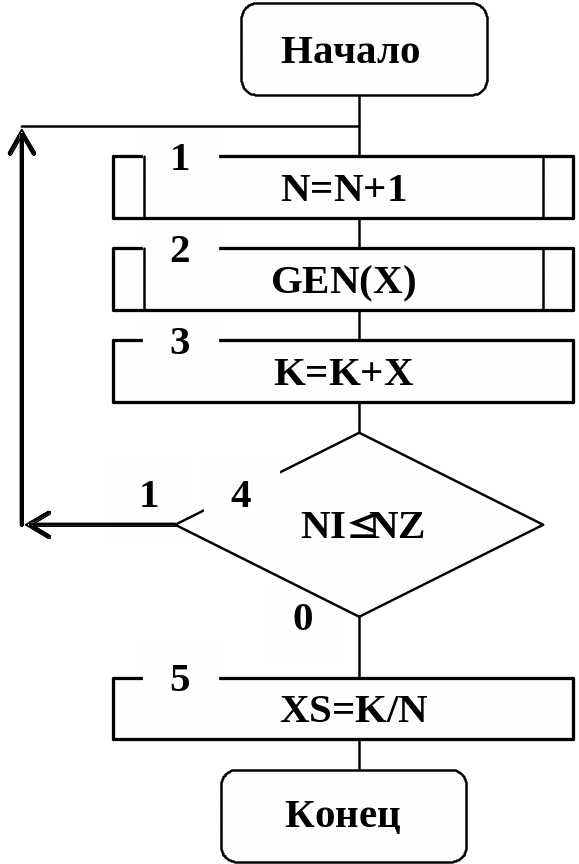
Рис. 5.9

В этом алгоритме N - такты моделирования; NZ - заданное число тактов моделирования; GEN(Х) – подпрограмма генерации случайной величины Х. После генерации всей выборки случайной величины Х в блоке 5 определяется среднее значение XS.

Оценкой S^2* дисперсии случайной величины определится

, (5.25)

где - математическое ожидание случайной величины.

Эта формула неудобна, т.к. в процессе моделирования необходимо запоминать весь массив значений х₁, х₂, х₃, …, х_N. Известна упрощенная формула, согласно которой

, (5.26)

т.е. для определения S^2* достаточно в двух счетчиках накапливать значения и . Для оценки корреляционного момента K_ случайных величин  и  с возможными значениями х_k и y_k применяется формула

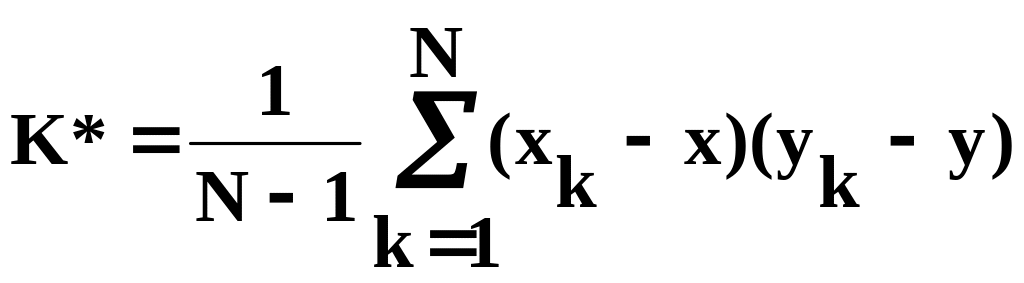. (5.27)

Эта формула преобразуется к виду

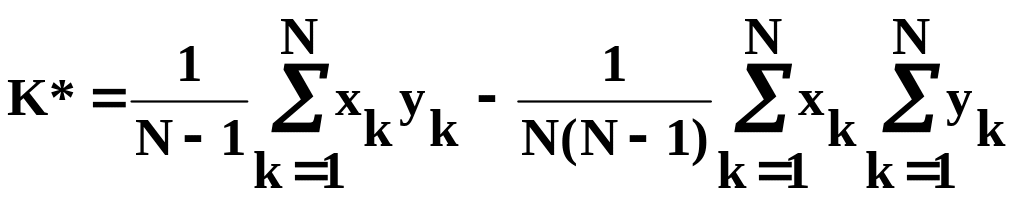, (5.28)

требующему подсчета и запоминания в трех счетчиках соответствующих величин:

, , .

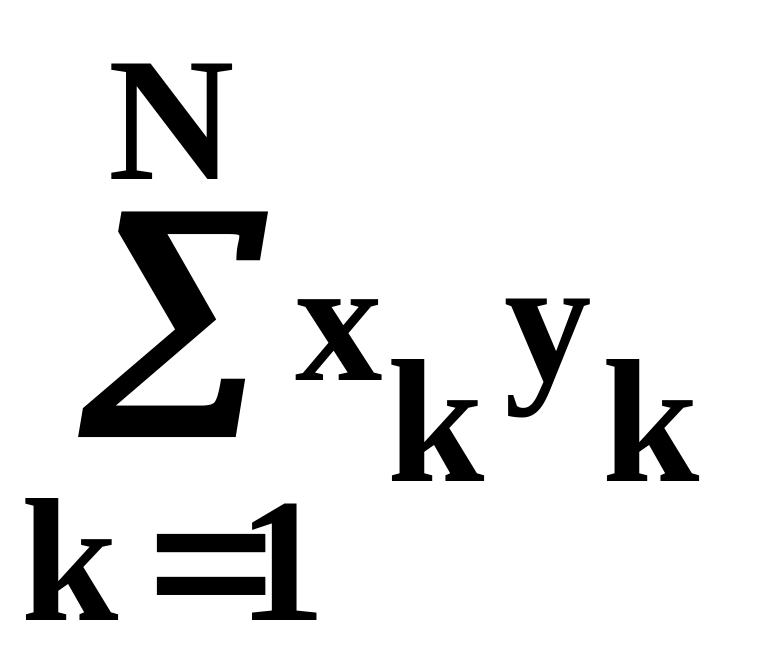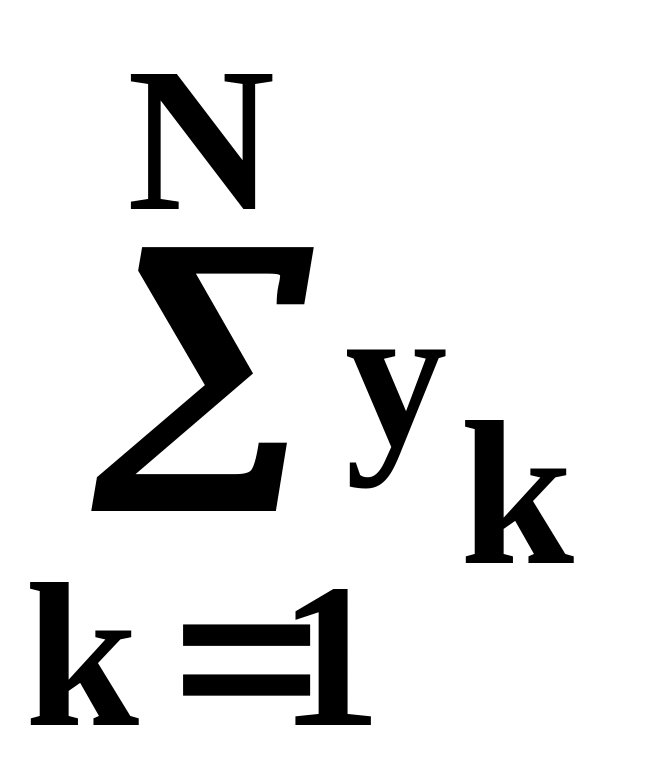Иногда искомыми величинами являются математическое ожидание и корреляционные функции случайного процесса Х(t). В теории случайных процессов изучаются закономерности изменения случайной величины от изменения неслучайного параметра, например времени, пространственной координаты и прочее. Основным понятием в теории вероятностей является понятие испытания с определенным множеством  возможных элементарных событий  - исходов испытания. Случайная величина X представляет однозначную числовую функцию X=f() элементарных событий, принимающего числовое значение в зависимости от исхода  испытания.

Пусть каждому элементу  множества  соответствует не одно определенное значение, а определенная числовая функция f_(t)(0,T) некоторого неслучайного параметра t. Так как для различных  эти функции различны, то каждую такую функцию f_(t) называют возможной реализацией случайного процесса Х(t). Совокупность всех возможных реализаций, т.е. множество функций f_(t) образуют случайный процесс Х(t).

Распределение вероятностей случайного процесса Х(t) задают распределением вероятностей случайных величин Х(t₁), Х(t₂), …, Х(t_s), соответствующих любому конечному набору значений t₁, t₂, …, t_s параметра t (s=1,2,3,…).

На практике случайный процесс Х(t) определяют математическим ожиданием и дисперсией, являющимися функциями параметра t, а также корреляционной функцией. Рассмотрим, как определяют и как вычисляют эти функции. На рис. 5.10 показаны возможные реализации случайного процесса Х(t).

Математическим ожиданием случайного процесса Х(t) называется неслучайная функция МХ(t), значение которой при каждом значении t=t_i равно математическому ожиданию МХ(t_i) той случайной величины Х(t_i), которая соответствует этому значению параметра.

Рис. 5.10

Математическое ожидание МХ(t) (см. рис. 5.10) представляет собой среднюю функцию, около которой группируются возможные реализации случайного процесса Х(t).

Дисперсией случайного процесса Х(t) называется неслучайная функция DХ(t), значение которой при каждом значении t=t_i параметра t равно математическому ожиданию DХ(t_i) той случайной величины Х(t_i), которая соответствует значению параметра t_i. Квадратный корень из дисперсии представляет среднее квадратичное отклонение случайного процесса Х(t) и определяется по формуле

. (5.29)

Связь между случайными величинами Х(t^*) и Х(t^**), соответствующим значениям t^* и t^** случайного процесса Х(t), характеризуется их ковариацией

B_X(t^*,t^**)=cov[Х(t^*),Х(t^**)]=

=M{[Х(t^*)-MХ(t^*)][Х(t^**)-MХ(t^**)]}. (5.30)

Ковариация представляет собой неслучайную функцию B_X(t^*,t^**) двух переменных t^* и t^**, которая графически может быть представлена поверхностью, как это показано на рис. 5.11.

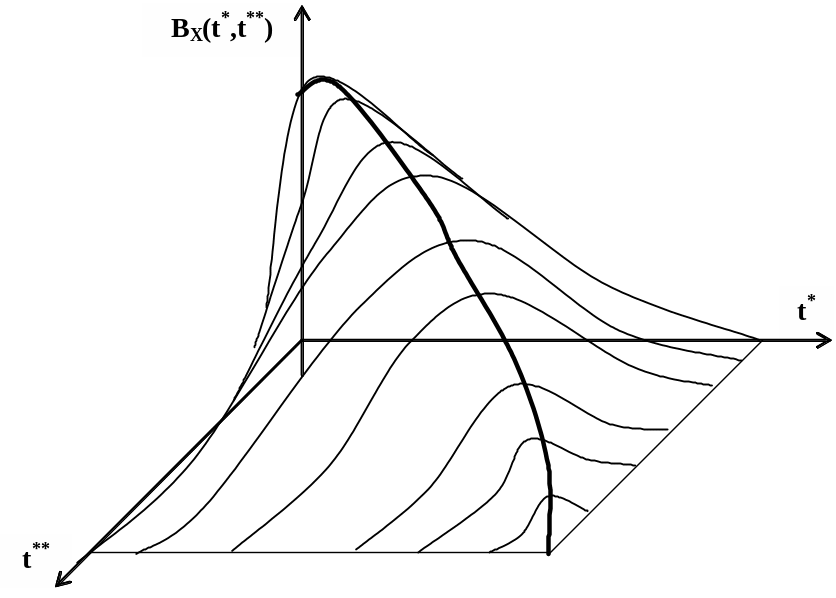
Рис. 5.11

Функция B_X(t^*,t^**) называется корреляционной функцией или автокорреляционной функцией случайного процесса Х(t).

Интересующий интервал (0,T) разбивается на части с шагом t. Накапливают значения Х_k(t_i) реализаций случайного процесса Х(t) для фиксированных моментов времени t_i. Затем вычисляют оценки для математического ожидания по формуле

. (5.29)

Оценки для корреляционной функции B_X(t^*,t^**) вычисляются по формуле

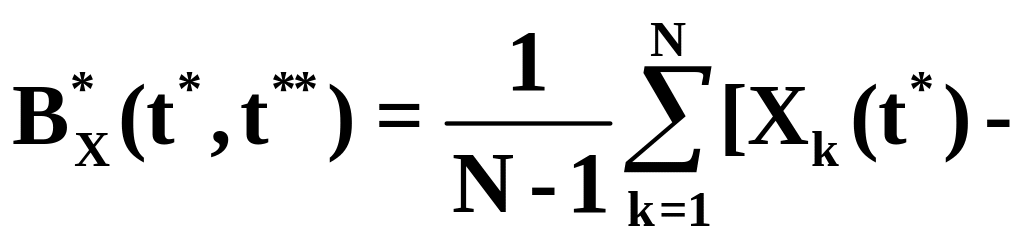
, (5.30)

где t^* и t^** «пробегают» все значения t. Так при моделировании при применении формулы (5.30) необходимо накапливать N значений X_k(t^*) и N значений X_k(t^**). На практике для оценки корреляционной функции B_X(t^*,t^**) применяют формулу

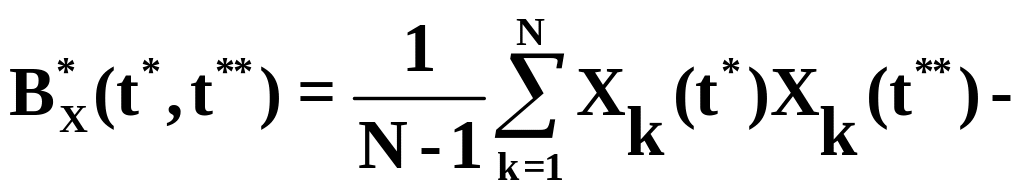
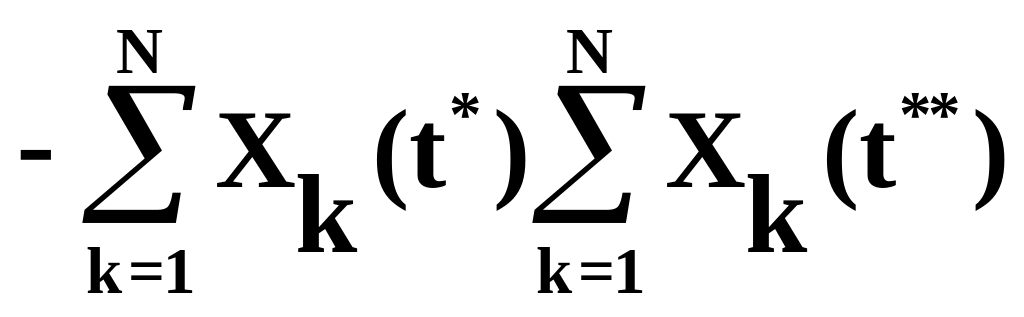. (5.31)

При применении формулы (5.31) необходимо три счетчика для подсчета сумм

, , .