5. Обработка результатов моделирования на эвм

5.1. Выбор числа опытов

При разработке имитационных моделей для исследования случайных объектов существует задача выбора числа опытов (объема выборки). Это непростая задача, т.к. во-первых, необходимо обосновать достоверность результатов моделирования и связать достоверность с точностью, а во-вторых, существуют события, вероятность появления которых очень мала (Р0) или, наоборот очень велика (Р1). Для обоснования объема выборки при имитационном моделировании применяют аналитические подходы [8,12,13].

В инженерной практике известны критерии для оценки погрешности. Непрерывную (аналоговую) величину х(t) в ряде инженерных задач рассматривают как дискретную, как показано на рис. 5.1.

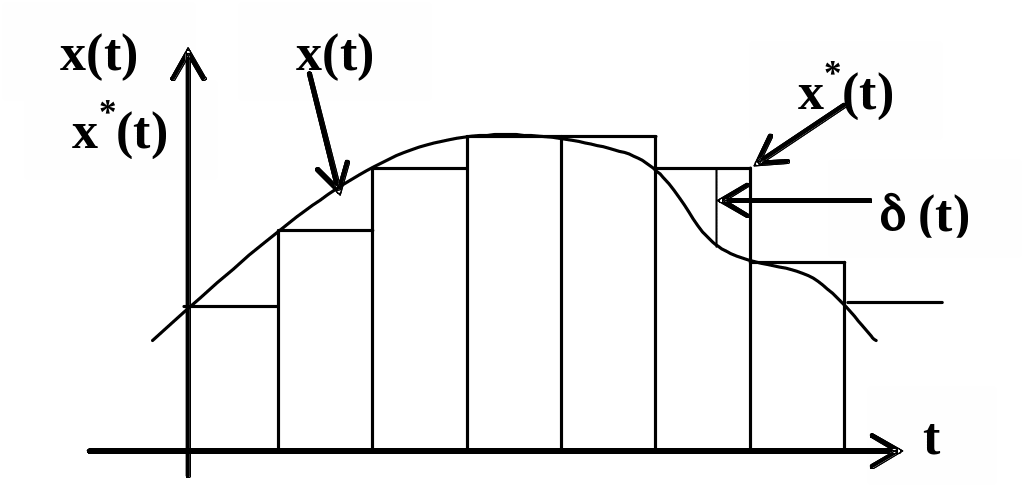
Рис. 5.1

Если х^*(t) - результат измерения непрерывной величины х(t), то для любого момента t текущая погрешность дискретизации этой непрерывной величины определится: (t)=х(t)-х^*(t). Выбор критерия оценки (t) зависит от назначения величины х(t). Известны следующие критерии.

Критерий наибольшего отклонения имеет вид

. Критерий применим, если известны априорные сведения о сигнале в форме условия Липшица , где l -некоторая константа.

Среднеквадратичный критерий приближения определяется по формуле

.

Среднеквадратичный критерий применим для функций, интегрируемых в квадрате. Использование среднеквадратичного критерия связано с усложнениями, например аппаратуры измерения, по сравнению с критерием наибольшего отклонения.

Интегральный критерий как мера отклонения х(t) от х^*(t) имеет вид

.

Если моделируются случайные процессы, то выше-названные критерии не применимы.

Выбор количества реализаций зависит от того, какие требования предъявляются к результатам моделирования.

Пусть для оценки случайной величины A, оцениваемой по результатам моделирования х, выбирается величина х^*, являющаяся функцией от х. Значения х^* будут отличаться от A в силу случайных факторов, т.е. можно связать точность оценки, теоретическое значение случайной величины A и её статистическую оценку х^* в виде формулы

|A-х*|<, (5.1)

где  - точность оценки.

В силу того, что каждый результат х^* моделирования случайной величины A также является случайной величиной, то вероятность того, что неравенство (5.1) выполняется, будет достоверностью точности оценки х^* случайной величины A, т.е. справедлива формула

Р(|A-х*|<e)=. (5.2)

Воспользуемся сформулированным критерием (5.2) для определения точности результатов методом статистического моделирования. Пусть цель моделирования - вычисление вероятности р появления события A. Количество  наступления события A в реализации процесса является случайной величиной, принимающей значение х₁=1 с вероятностью р и значение х₂=0 с вероятностью 1-р. Пример случайного появления события A показан на рис. 5.2.

Рис. 5.2

Математическое ожидание случайной величины  определится по формуле

M[]=х₁р+х₂(1-р)=р. (5.3)

Если х₁=1, как появление события A, а х₂=0, как не появление события, то значение M[] совпадает с вероятностью р наступления события A.

Дисперсия определится по формуле

D[]=[х₁-M[]]²р+[х₂-M[]]²(1-р)=р(1-р). (5.4)

При выполнении имитационного моделирования оценкой вероятности р является частость m/N наступления события A при N реализациях, m - число испытаний, в которых событие A наступило. Частость m/N определяется формулой

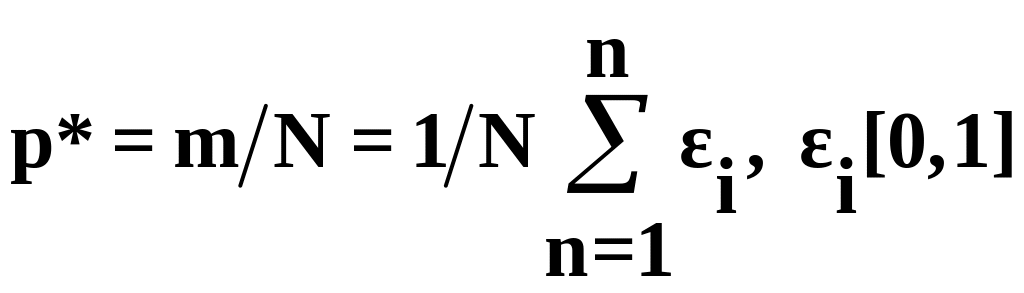, (5.5)

где _i - количество наступлений событий A в реализации с номером i.

Из формул (5.3), (5.4) и (5.5) можно определить математическое ожидание и дисперсию частости m/N

. (5.6)

В силу центральной предельной теоремы вероятностей частость m/N при N имеет распределение, близкое к нормальному. Поэтому для каждого значения достоверности  (вероятности) можно выбрать из таблиц нормального распределения такую величину (значение случайной величины) t_, что точность  будет равна

(5.7)

Подставив в формулу (5.7) значение D из формулы (5.6), получим

(5.8)

Из формулы (5.8) можно определить количество реализаций N, необходимых для получения оценки m/N с точностью  и достоверностью :

(5.9)

В формуле (5.9) неизвестны величины N и р, т.к. вероятность р определяется, исходя из ее оценки m/N, а N - число необходимых для этого опытов. Поэтому в практике моделирования для определения N поступают следующим образом. Выбирают N₀=50-100. По результатам N₀ реализаций определяют m/N₀, т.е. осуществляют примерную оценку вероятности р=m/N₀. Затем по формуле (5.9) окончательно выбирают N, принимая р=m/N.

Другим случаем является оценка по результатам моделирования среднего значения некоторой случайной величины. Пусть непрерывная случайная величина A имеет среднее значение и дисперсию ². В реализации с номером i случайная величина A принимает значение х_i. В качестве оценки для среднего значения (математического ожидания) A используется среднее арифметическое

.

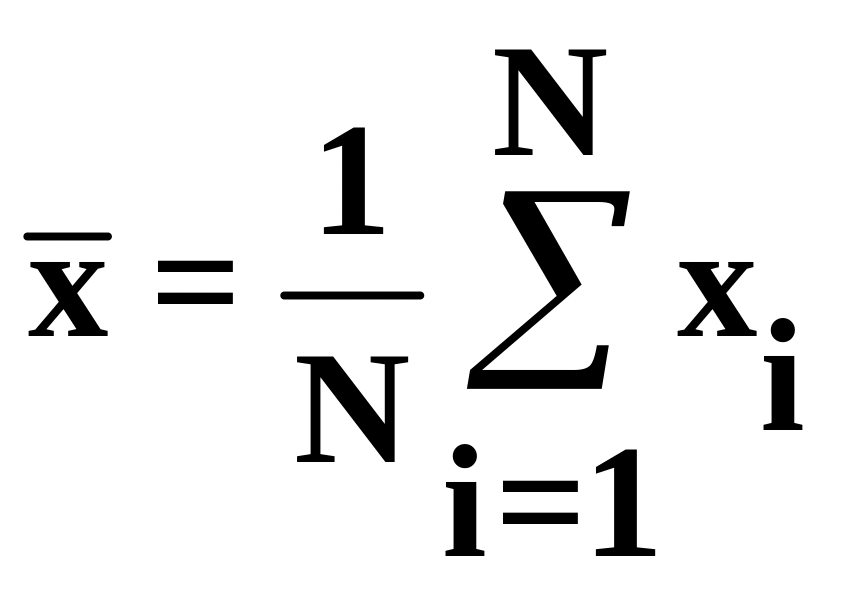В силу центральной предельной теоремы при N будет иметь приблизительно нормальное распределение с математическим ожиданием и дисперсией ²/N, поэтому точность определится по формуле

.

Число реализаций определится по формуле

. (5.10)

Так как в формуле (5.10) неизвестными являются число реализаций N и среднеквадратичное отклонение ², то также выбирают N₀=50-100. По результатам N₀ реализаций определяют оценку дисперсии, а затем по формуле (5.10) окончательно выбирают N. Количество реализаций N в формуле (5.9) зависит от р, а в формуле (5.10) от ².

Целесообразно так строить моделирующий алгоритм, чтобы методом моделирования оценивались параметры величин, имеющих возможно меньшую дисперсию, или вероятности случайных событий, не близкие к 0,5. Вероятности не должны быть также близки к 0 или 1, т.к. в этом случае снижается эффективность имитационного моделирования.