4.3. Проверочные тесты

Программная реализация датчика псевдослучайных, квазиравномерно распределенных чисел может быть получена любым программистом на основе разработанного им алгоритма с применением либо аналитических методов, либо методов перемешивания. Качество датчика необходимо проверить. Осуществляются проверки путем применения проверочных тестов. Рассмотрим проверочные тесты.

Тест частот. Отрезок [0,1] разбивается на m (обычно 10-20) равных интервалов, как это показано на рис. 4.6.

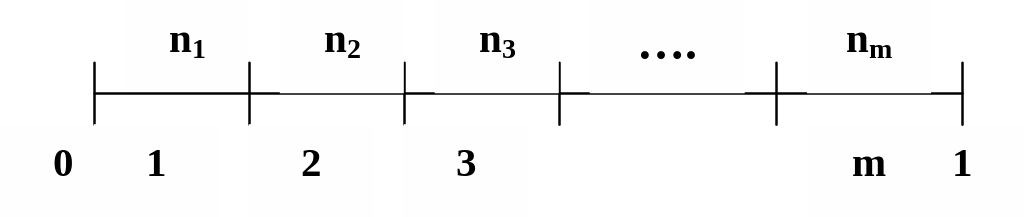
Рис. 4.6

Датчик псевдослучайных, квазиравномерно распределенных чисел генерирует N величин, каждая из которых принадлежит одному из m отрезков.

В результате проведения N испытаний будут получены эмпирические частоты n_i, представляющие собой число попаданий чисел датчика в интервал i, i= . Деление частот n_i на число опытов N даст эмпирические частоты.

Если рассматривать теоретическое равномерное распределение случайной величины на отрезке [0,1], то теоретические вероятности попадания в каждый из m отрезков одинаковы и равны значению 1/m.

Для проверки согласия датчика псевдослучайных, квазиравномерно распределенных чисел и теоретического равномерного распределения полученные эмпирические частости n_i/N, (i= ), 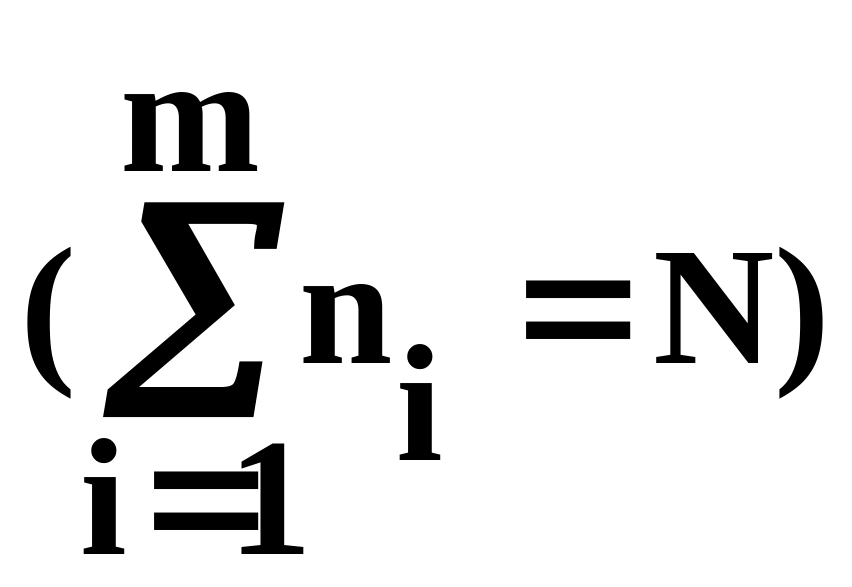сравнивают с теоретическими вероятностями 1/m. Согласие проверяется по критерию ², т.к. случайная величина

(4.7)

подчиняется распределению ² с (m-1) степенями свободы, где N - объем выборки (число опытов).

На рис. 4.7 приведен алгоритм теста частот. Рассмотрим его работу.

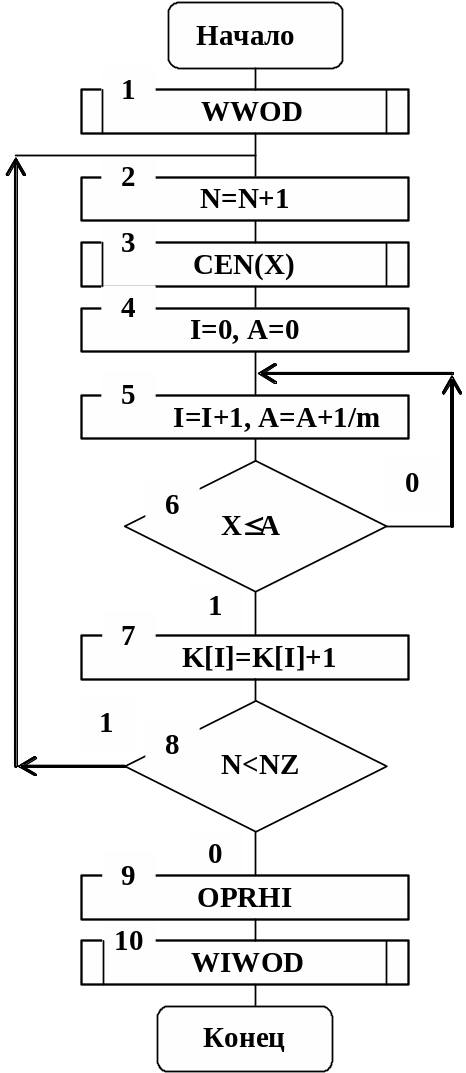
Рис. 4.7

В подпрограмме WWOD осуществляется ввод исходных данных для моделирования: N=0 - начальный такт моделирования; NZ - заданное число тактов моделирования (число опытов); m – число интервалов разбиения отрезка [0,1]. В подпрограмме WWOD также осуществляется обнуление необходимых для работы идентификаторов и счетчиков.

В блоке 2 происходит наращивание тактов моделирования. В блоке 3 датчиком случайных чисел генерируется число Х. Затем это число Х сравнивается с правыми границами интервалов разбиения отрезка [0,1]. Для этого в блоках 4 - 6 организован цикл по переменной I и сравнение числа Х с числом А, которое последовательно принимает значения: 1/m, 2/m, 3/m, …, m/m.

При выполнении условия ХA содержимое соответствующего счетчика увеличивается на единицу (см. блок 7).

В блоке 8 осуществляются проверки выполнения числа опытов. Если датчик псевдослучайных, квазиравномерно распределенных чисел выполнил генерацию заданного числа опытов NZ, то в блоке 9 происходит вычисление случайной величины ².

В подпрограмме WIWOD (см. блок 10) на экран дисплея выводятся значения случайной величины ², счетчиков K[I], в которых подсчитаны частоты n_i, а также могут быть выведены гистограммы эмпирических частостей =n_i/N=K[I]/NZ, как это показано на рис. 4.8.

На рис. 4.8 приведены гистограммы для заданного числа опытов NZ =10000. Очевидно, что форма гистограммы частот должна совпадать с формой гистограммы частостей, т.к. эмпирические частости определяются по формуле =K[I]/NZ.

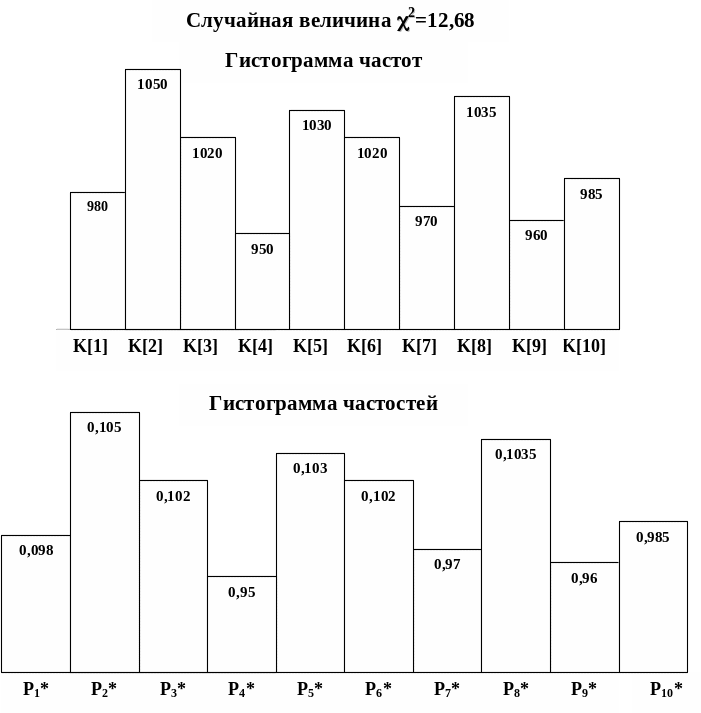
Рис. 4.8

Тесты пар частот. Пусть датчик псевдослучайных, квазиравномерно распределенных чисел генерирует последовательность чисел Х₁,Х₂,...,Х_N. Рассматриваются последовательные пары случайных чисел. Квадрат со сторонами [0,1] на [0,1] делится на m² частей, как это показано на рис. 4.9.

Если пары образовать в виде (Х₁,Х₂), (Х₃,Х₄)..., то каждая пара случайно попадает в одно из m² делений квадратной таблицы. Пары (Х₁,Х₂), (Х₃,Х₄)... взаимно независимы и результат их попадания в одно из m² делений квадратной таблицы оценивается эмпирической частотой n_ij.

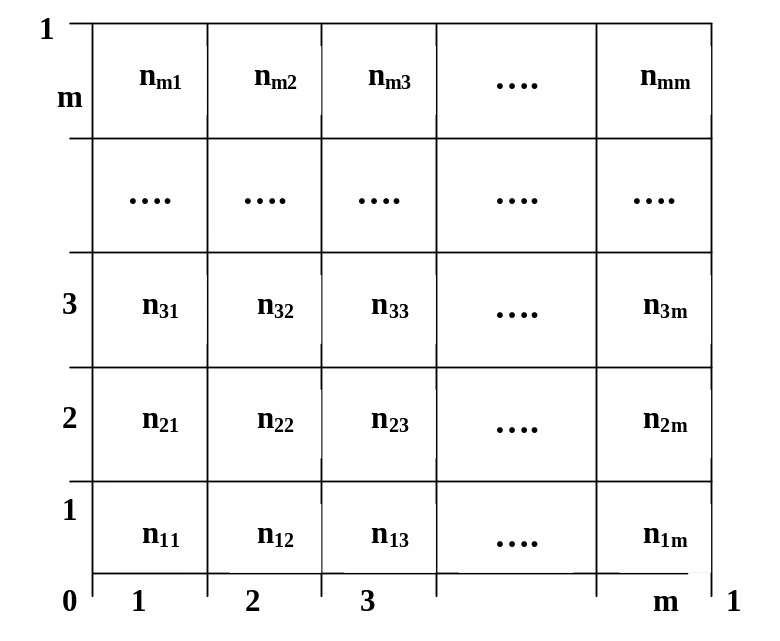
Рис. 4.9

Если рассматривать теоретическое равномерное распределение случайной величины на отрезке [0,1] и образование из чисел таких же пар, то теоретические вероятности попадания в каждый из m² делений квадратной таблицы одинаковы и равны значению 1/m².

Для проверки согласия по данному тесту пар частот датчика псевдослучайных, квазиравномерно распределенных чисел и теоретического равномерного распределения полученные эмпирические частости 2n_ij/N, (i,j= ), сравнивают с теоретическими вероятностями 1/m². Согласие проверяется по критерию ², т.к. случайная величина

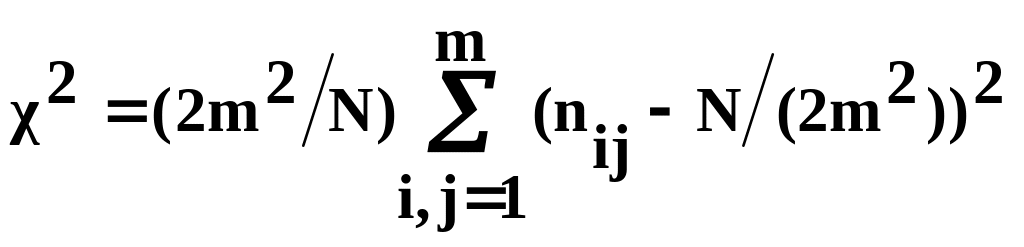(4.8)

распределена по закону ² с (m²-m) степенями свободы, где N/2 - объем выборки пар случайных величин, генерированных датчиком псевдослучайных, квазиравномерно распределенных чисел. На рис. 4.10 приведен алгоритм для рассмотренного теста пар частот.

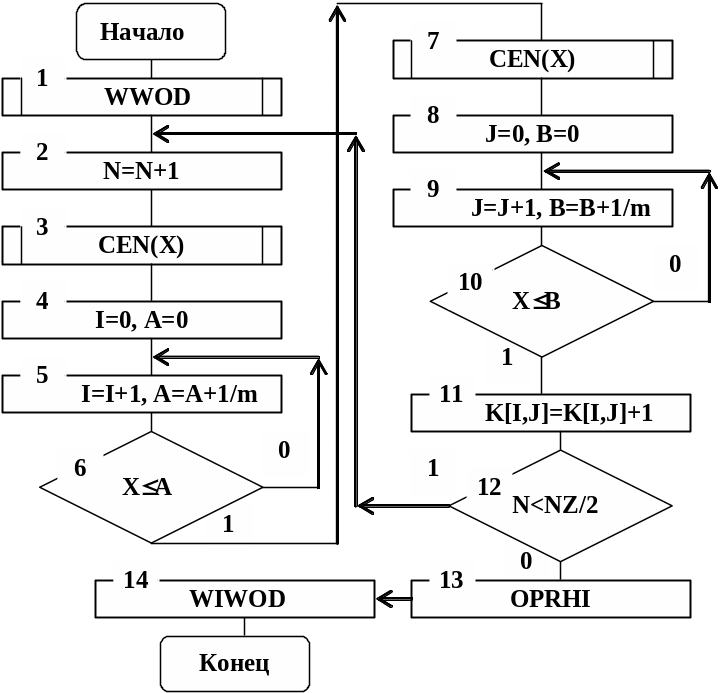
Рис. 4.10

В подпрограмме WWOD осуществляется ввод исходных данных для моделирования:

- N=0 - начальный такт моделирования;

- NZ - заданное число тактов моделирования;

- m - число интервалов разбиения отрезка [0,1], происходит обнуление необходимых для работы идентификаторов и счетчиков.

В блоке 2 происходит наращивание тактов моделирования. В блоке 3 датчиком случайных чисел генерируется число Х. Затем в блоках 4 – 6 определяется индекс I. В блоке 7 датчиком случайных чисел генерируется второе число Х (тем самым образована пара (Х₁,Х₂)). В блоках 8 – 10 определяется индекс J.

В блоке 11 в счетчиках K[I,J] осуществляется подсчет частот попадания случайных пар (Х_k,Х_р) в соответствующие деления квадратной таблицы. В блоке 12 осуществляются проверки выполнения числа опытов. Если датчик псевдослучайных, квазиравномерно распределенных чисел выполнил генерацию заданного числа опытов NZ/2, то в блоке 13 происходит вычисление случайной величины ². В подпрограмме WIWOD (см. блок 14) на экран дисплея выводятся значения случайной величины ², счетчиков K[I,J], значения эмпирических частостей =2n_ij/N=2K[I,J]/NZ. Генерируемая выборка в данном методе используется неэффективно. Можно пары образовать в следующем виде (Х₁,Х₂),(Х₂,Х₃),(Х₃,Х₄),... .

Этот метод образования пар более эффективен, т.к. полнее использует выборку чисел, но из-за зависимостей пар случайная величина ² определится по формуле

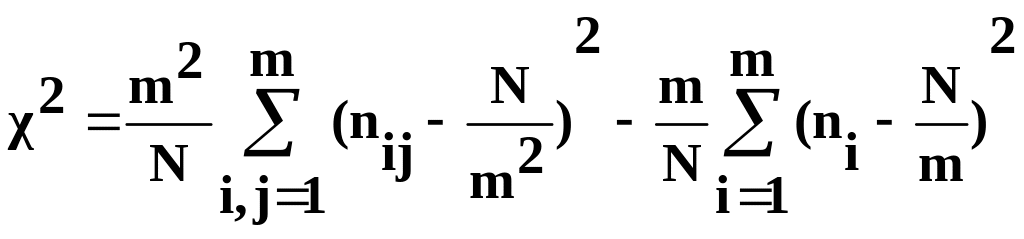], (4.9)

где .

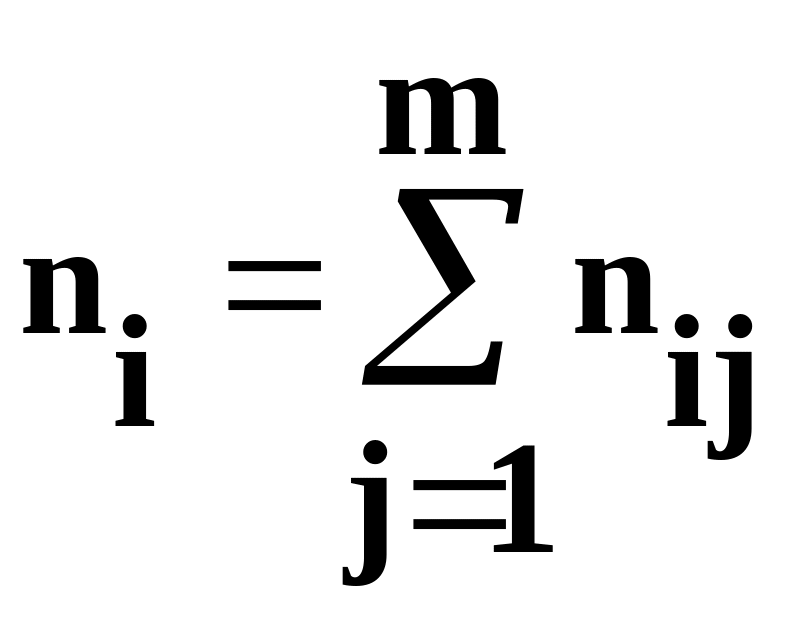Случайная величина ² будет определена распределением ² с (m²-m) степенями свободы.

На рис. 4.11 приведен алгоритм для рассмотренного теста пар частот с эффективным использованием выборки.

Рис. 4.11

В данном алгоритме в блоке 2 генрируется число Х₁, а затем в блоках 3 - 5 определяется индекс I. В блоке 6 происходит наращивание тактов моделирования. В блоке 7 датчиком случайных чисел генерируется число Х. В блоках 8 – 10 определяется индекс J (тем самым образована пара (Х₁,Х₂)). В блоке 11 в счетчиках K[I,J] осуществляется подсчет частот попадания случайных пар в деления квадратной таблицы. В блоке 12 индексу I присваивается значение индекса J. При N=2 будет образована пара (Х₂,Х₃) и т.д.