5.1. Аппроксимация частотных характеристик
ВОПРОС 5.1.1/к2. Z-преобразование связано с деформацией частотной шкалы непрерывных функций в частотную шкалу главного частотного диапазона цифровых функций. В какой шкале задаются значения граничных частот фильтрации при проектировании рекурсивных фильтров? 1- цифровых функций.
ВОПРОС 5.1.2/к2. Z-преобразование связано с деформацией частотной шкалы непрерывных функций в частотную шкалу главного частотного диапазона цифровых функций. В какой шкале задается аппроксимация передаточной функции при проектировании рекурсивных фильтров? 2- непрерывных функций.
ВОПРОС 5.1.3/к2. Z-преобразование связано с деформацией частотной шкалы непрерывных функций в частотную шкалу главного частотного диапазона цифровых функций. Какие значения граничных частот фильтрации задается при аппроксимации передаточной функции рекурсивных фильтров? 2- деформированные частоты фильтрации.
ВОПРОС 5.1.4/к2. По какому аргументу задается аппроксимация передаточной функции при проектировании рекурсивных цифровых фильтров?
3- по относительной частоте фильтрации.
ВОПРОС 5.1.5/к2. По какой частоте нормируется аппроксимация передаточной функции при проектировании рекурсивных цифровых фильтров нижних частот? 3- по частоте среза фильтра H() = 0.707.
ВОПРОС 5.1.6/к3. В какой форме задается аппроксимация передаточной функции при проектировании низкочастотных (или высокочастотных) рекурсивных цифровых фильтров? 4- |H(c)|2.
ВОПРОС 5.1.7/к3. Крутизна среза низкочастотного рекурсивного цифрового фильтра задана порядка 1000 на октаву (60 дб). Какой порядок будет иметь фильтр?
Ответ – 10.
ВОПРОС 5.1.8/к3. Крутизна среза низкочастотного рекурсивного цифрового фильтра задана порядка 100 на октаву (40 дб). Какой порядок будет иметь фильтр?
Ответ – 7.
ВОПРОС 5.1.9/к3. В какой форме задается аппроксимация передаточной функции при проектировании цифрового фильтра Баттеруорта низких частот?
2: 1/[1+(c)2N].
ВОПРОС 5.1.10/к3. В какой форме задается аппроксимация передаточной функции при проектировании цифрового фильтра Баттеруорта высоких частот?
3: (c)2N/[1+(c)2N].
ВОПРОС 5.1.11/к3. Выполняется расчет фильтра Баттеруорта порядка N=4. Сколько полюсов должен иметь фильтр?
Ответ – 8.
ВОПРОС 5.1.12/к3. Выполняется расчет фильтра Баттеруорта порядка N=5. Сколько биквадратных блоков (секций свертки) должен иметь фильтр? Ответ – 5.
6.1. Понятия и особенности деконволюции
ВОПРОС 6.1.1/к2. Система задана конечным оператором h(n). С использованием какой формулы вычисляется оператор деконволюции данной системы?
2: 1).
ВОПРОС 6.1.2/к3. Система задана конечным оператором h(n). С использованием какой формулы вычисляется оптимальный оператор деконволюции данной системы? 4: H*()/А().
ВОПРОС 6.1.3/к3. Система задана
конечным оператором h(n).
С использованием какой формулы
вычисляется рекурсивный оператор
деконволюции данной системы? 5: 1/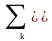
hk
zk
ВОПРОС 6.1.4/к3. Система задана конечным оператором h(n). С использованием какой формулы вычисляется оператор неполной деконволюции данной системы (оператор сжатия сигналов)?
6: H*()/[|H()|2+g2].
ВОПРОС 6.1.5/к2. Система задана конечным оператором h(n). К какому типу относится оператор деконволюции данной системы? 3: В общем случае бесконечный, но может быть и конечным.
ВОПРОС 6.1.6/к3. Система задана оператором h(n)↔H(). При каких условиях оператор деконволюции данной системы является неустойчивым? 4: H() имеет нулевые точки.
ВОПРОС 6.1.7/к3. Система задана оператором h(n)↔H(). При каких условиях оператор деконволюции данной системы затухает медленно? 4: H() имеет значения, близкие к нулевым.
ВОПРОС 6.1.8/к2. Какой коэффициент усиления дисперсии шумов является характерным (обычным) для операторов деконволюции и фильтров сжатия сигналов? 4: Много больше 1.
ВОПРОС 6.1.9/к2. Система задана конечным оператором h(n)↔H(). На основе какого выражения может быть выполнена инверсия оператора? 3: h(n) * h-1(n) = o(n).
ВОПРОС 6.1.10/к2. Может ли быть реализован оператор деконволюции с бесконечным импульсным откликом?