4: Зависит от ширины полосы и ее положения в главном частотном диапазоне.

ВОПРОС 3.2.18/к2. Необходимо ли применение весовых функций при синтезе низкочастотных и полосовых дифференцирующих фильтров? 1- да,

ВОПРОС 3.2.19/к2. Возможен ли синтез абсолютно гладких полосовых нерекурсивных частотных фильтров? 1- да,

4.1. Принципы рекурсивной фильтрации

ВОПРОС 4.1.1/к2. Какой подстановкой значения z выполняется преобразование z-образа фильтра в его частотную характеристику? 1: exp(-jt).

В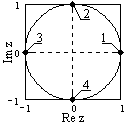 ОПРОС 4.1.2/к2. На рисунке - модуль функции z=exp(-jt) в z-плоскости. Какой точке плоскости соответствует частота =0? Ответ – 1.

В ОПРОС 4.1.3/к2. На рисунке - модуль функции z=exp(-jt) в z-плоскости. Какой точке плоскости соответствует частота =/2? ОТВЕТ-2

В ОПРОС 4.1.4/к2. На рисунке - модуль функции z=exp(-jt) в z-плоскости. Какой точке плоскости соответствует частота =?

Ответ – 3.

В ОПРОС 4.1.5/к2. На рисунке - модуль функции z=exp(-jt) в z-плоскости. Какой точке плоскости соответствует частота = -/2?

Ответ – 4.

В ОПРОС 4.1.6/к2. На рисунке - модуль функции z=exp(-jt) в z-плоскости. Какой точке плоскости соответствует частота = - ?

Ответ – 3.

ВОПРОС 4.1.7/к2. Рекурсивная система задана уравнением:

y(k) = b_n s(k-n) +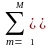 a_m y(k-m), N=М=1, b₀=0.8, b₁=0.2, а₁=0.5.

Вычислите значение h₂ импульсного отклика системы? Ответ – 0.3.

ВОПРОС 4.1.8/к2. Рекурсивная система задана уравнением:

y(k) = b_n s(k-n) + a_m y(k-m), N=М=1, b₀=0.8, b₁=0.2, а₁=0.5.

Вычислите значение h₃ импульсного отклика системы? Ответ – 0.15.

ВОПРОС 4.1.9/к2. Рекурсивная система задана уравнением:

y(k) = b_n s(k-n) + a_m y(k-m), N=М=1, b₀=0.8, b₁=0.2, а₁=0.5.

Конечным или бесконечным является импульсный отклик системы? 2: Бесконечным.

ВОПРОС 4.1.10/к2. Можно ли реализовать рекурсивную цифровую фильтрацию данных без сдвига фазы? 4- да, двойной фильтрацией с реверсированием данных

4.2. Синтез операторов фильтров

ВОПРОС 4.2.1/к2. Укажите уравнение системы при реализации рекурсивного цифрового фильтра в каскадной форме.

1: .

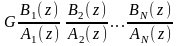ВОПРОС 4.2.2/к2. Укажите уравнение системы при реализации рекурсивного цифрового фильтра в параллельной форме.

2: H_o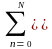(z) B_n(z) / [1+A_n(z)].

ВОПРОС 4.2.3/к1. Под каким углом в z-плоскости находится радиус-вектор нуля и полюса передаточной функции рекурсивного цифрового фильтра режекции постоянной составляющей данных? 1- 0^о.

ВОПРОС 4.2.4/к1. Сколько пар нулей и полюсов имеет передаточная функция рекурсивного цифрового фильтра режекции постоянной составляющей данных?

Ответ – 1.

ВОПРОС 4.2.5/к1. Сколько пар нулей и полюсов имеет передаточная функция рекурсивного цифрового фильтра режекции частоты Найквиста в данных? Ответ – 1.

ВОПРОС 4.2.6/к1. Под какими углами в z-плоскости находятся радиус-векторы нулей и полюсов передаточной функции рекурсивного цифрового фильтра режекции произвольной частоты в данных?

4- определяется расчетом.

ВОПРОС 4.2.7/к1. Сколько пар нулей и полюсов имеет передаточная функция рекурсивного цифрового фильтра режекции произвольной частоты в данных?

Ответ – 2.

ВОПРОС 4.2.8/к2. Как зависит ширина полосы пропускания  (на половине высоты) рекурсивного цифрового фильтра режекции произвольной частоты  в данных от расстояния R между полюсом и нулем? 1- чем меньше R, тем меньше ,

ВОПРОС 4.2.9/к2. Как зависит длительность импульсной реакции h рекурсивного цифрового фильтра режекции произвольной частоты в данных от расстояния R между полюсом и нулем?

2- чем меньше R, тем больше h,

ВОПРОС 4.2.10/к1. Сколько пар нулей и полюсов (в сумме) имеет передаточная функция рекурсивного цифрового фильтра селекции произвольной частоты в данных? Ответ – 2.