3.2. Синтез операторов фильтров

ВОПРОС 3.2.1/к3. При усечении операторов идеальных частотных фильтров на скачках передаточных функций операторов возникает явление Гиббса. Как можно нейтрализовать явление Гиббса? 3- Умножением оператора на весовую функцию.

ВОПРОС 3.2.2/к1. Что является исходным заданием при проектировании операторов нерекурсивных частотных фильтров? 2- Частотная характеристика оператора фильтра.

ВОПРОС 3.2.3/к2. Вашим заданием при проектировании нерекурсивного частотного цифрового фильтра ограничено количество членов фильтра окном (2N+1). Какую минимальную ширину переходной зоны можно достигнуть таким оператором без применения весовых функций? 1- 2/(2N+1).

ВОПРОС 3.2.4/к3. Вашим заданием при проектировании нерекурсивного частотного цифрового фильтра ограничено количество членов фильтра окном (2N+1). Какую минимальную ширину переходной зоны можно достигнуть таким оператором c применением весовых функций?

3  2/(N+1).

ВОПРОС 3.2.5/к2. Какой параметр задания при проектировании нерекурсивного частотного цифрового фильтра определяет количество членов фильтра (окно (2N+1))? 3- Ширина переходной зоны.

ВОПРОС 3.2.6/к3. По какой из формул следует выполнять расчет оператора нерекурсивного цифрового фильтра произвольного назначения?

2: (1/2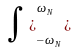) H()exp(jn/_N) d

ВОПРОС 3.2.7/к3. По какой из формул следует выполнять расчет оператора нерекурсивного цифрового фильтра произвольного назначения, работающего без сдвига фазы?

3: (1/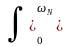) H() cos(n/_N) d.

ВОПРОС 3.2.8/к3. По какой из формул следует выполнять расчет симметричного оператора низкочастотного нерекурсивного цифрового фильтра?

4: (1/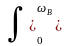) H() cos(n/_N) d

ВОПРОС 3.2.9/к3. По какой из формул следует выполнять расчет симметричного оператора высокочастотного нерекурсивного цифрового фильтра?

5: (1/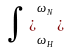) H() cos(n/_N) d

ВОПРОС 3.2.10/к3. Для нейтрализации явления Гиббса на передаточной функции H() нерекурсивного цифрового фильтра h(n) применена весовая функция p(n)  P(). По какой из формул производится нейтрализация явления Гиббса?

2: h(n)·p(n).

ВОПРОС 3.2.11/к4. Укажите уравнение оператора точного дифференцирования сигнала? 1: j,

ВОПРОС 3.2.12/к4. Укажите уравнение оператора точного вычисления второй производной сигнала? 5: (-²),

ВОПРОС 3.2.13/к3. Чему равна сумма коэффициентов операторов дифференцирующих фильтров? 1- нулю.

ВОПРОС 3.2.14/к3. Чему равен коэффициент усиления постоянной составляющей входных данных при использовании операторов дифференцирующих фильтров? 1- нулю.

ВОПРОС 3.2.15/к2. Может ли быть реализована линейная частотная характеристика дифференцирующего фильтра для определенного частотного интервала входных данных? 1- да,

ВОПРОС 3.2.16/к2. Являются ли дифференцирующие фильтры фазосдвигающими? 2- нет,

ВОПРОС 3.2.17/к2. Какое значение коэффициента усиления дисперсии шумов характерно для операторов полосовых частотных дифференцирующих фильтров?