2.2. Специальные фильтры обработки данных
ВОПРОС 2.2.1/к3. Как при дифференцировании сигнала изменяется его спектр в области низких (НЧ) и высоких (ВЧ) частот? 3: амплитуды ВЧ возрастают, а НЧ уменьшаются,
ВОПРОС 2.2.2/к3. Как при интегрировании сигнала изменяется его спектр в области низких (НЧ) и высоких (ВЧ) частот? 5: амплитуды НЧ возрастают, ВЧ уменьшаются,
ВОПРОС 2.2.3/к2. К какому типу фильтров относятся разностные операторы?
3- каузальные.
ВОПРОС 2.2.4/к2. К какому типу функций относятся частотные характеристики разностных операторов? 3- комплексные.
ВОПРОС 2.2.5/к2. К какому типу функций относятся частотные характеристики центрированных разностных операторов четного порядка? 1- реальные.
ВОПРОС 2.2.6/к2. Чему равна сумма коэффициентов оператора разностного фильтра? 1- нулю
ВОПРОС 2.2.7/к2. Чему равен коэффициент Кпс (усиления постоянной составляющей сигнала) разностного фильтра?
1- нулю.
ВОПРОС 2.2.8/к3. Могут ли разностные операторы выполнять фильтрацию сигналов без сдвига фазы?
2- Да, операторы четного порядка при центрировании.
ВОПРОС 2.2.9/к3. Как вычислить разностный оператор фильтра М произвольного М-порядка при М>1? 1- М-1 * 1.
ВОПРОС 2.2.10/к3. Многочлены какого порядка обнуляют разностные операторы М-порядка? 1: М-1
ВОПРОС 2.2.11/к2. Четными или нечетными являются операторы оценки первой производной (дифференцирования) сигналов? 2- нечетными.
ВОПРОС 2.2.12/к2. К какому типу функций относятся частотные характеристики операторов оценки первой производной (дифференцирования) сигналов? 2- мнимые
ВОПРОС 2.2.13/к3. Четными или нечетными являются операторы оценки второй производной (двукратного дифференцирования) сигналов? 1- четными
ВОПРОС 2.2.14/к3. К какому типу функций относятся частотные характеристики операторов оценки второй производной (дифференцирования) сигналов? 1- реальные.
ВОПРОС 2.2.15/к4. В каком интервале частот может находиться спектр числовых массивов при использовании операторов оценки первой производной данных? 1: 0-0.3,
ВОПРОС 2.2.16/к3. Какое значение коэффициента усиления дисперсии шумов характерно для операторов оценки первой производной данных? 1- меньше 1
ВОПРОС 2.2.17/к4. В каком интервале частот может находиться спектр числовых массивов при использовании операторов оценки второй производной данных? 1: 0-0.3,
ВОПРОС 2.2.18/к3. Какое значение коэффициента усиления дисперсии шумов характерно для операторов оценки второй производной данных? 4- много больше 1.
ВОПРОС 2.2.19/к4. Укажите уравнение оператора точного интегрирования сигнала?
2.= 1/(j),
3.1. Весовые функции
ВОПРОС 3.1.1/к2. При усечении операторов идеальных частотных фильтров на скачках передаточных функций операторов возникает явление Гиббса. Зависит ли амплитуда пульсаций явления Гиббса от ширины окна усеченного оператора? 2- нет.
ВОПРОС 3.1.2/к2. При усечении операторов идеальных частотных полосовых фильтров на скачках передаточных функций операторов возникает явление Гиббса. Зависит ли амплитуда пульсаций явления Гиббса от положения скачка в главном частотном диапазоне? 2- нет.
ВОПРОС 3.1.3/к3. При усечении операторов идеальных частотных фильтров на скачках передаточных функций операторов возникает явление Гиббса. Зависит ли частота пульсаций явления Гиббса от ширины окна усеченного оператора? 2- чем меньше окно, тем меньше частота пульсаций,
ВОПРОС 3.1.4/к2. При усечении операторов идеальных частотных полосовых фильтров на скачках передаточных функций операторов возникает явление Гиббса. Зависит ли частота пульсаций явления Гиббса от положения скачка в главном частотном диапазоне? 2- нет.
ВОПРОС 3.1.5/к4. Чему равен период пульсаций явления Гиббса в области скачков передаточных функций операторов цифровых частотных фильтров, усеченных до размера N (окно 2N+1)? 4: /(N+1).
ВОПРОС 3.1.6/к4. Чему равна амплитуда максимальной пульсации явления Гиббса в области скачков передаточных функций операторов цифровых частотных фильтров, усеченных до размера N (окно 2N+1), в % от амплитудного значения скачка? 9%,
ВОПРОС 3.1.7/к4. Чему равна ширина переходной зоны в области скачков передаточных функций операторов цифровых частотных фильтров, усеченных до размера N (окно 2N+1)? 4: /(N+1).
ВОПРОС 3.1.8/к2. Как зависит ширина переходной зоны на месте скачка передаточных функций операторов цифровых частотных фильтров, усеченных до размера N (окно 2N+1)? 1: Тем больше, чем меньше N.
ВОПРОС 3.1.9/к2. Как изменяется ширина переходной зоны на месте скачка передаточных функций операторов цифровых частотных фильтров, усеченных до размера N (окно 2N+1), при применении весовых функций для подавления пульсаций явления Гиббса? 2: Увеличивается
ВОПРОС 3.1.10/к2. Оператор цифрового частотного фильтров усечен до размера N (окно 2N+1). Каким должен быть размер окна весовой функции для подавления пульсаций явления Гиббса? 1: 2N+1.
ВОПРОС 3.1.11/к2. Какая из перечисленных весовых функций обеспечивает максимальное подавление пульсаций явления Гиббса? 5: Кайзера
ВОПРОС 3.1.12/к3. При усечении операторов идеальных частотных полосовых фильтров на скачках передаточных функций операторов возникает явление Гиббса. Может ли значение амплитуды выбросов явления Гиббса превышать 10% от величины скачка передаточной функции? 1- да,
ВОПРОС 3.1.13/к2. При усечении операторов идеальных низкочастотных фильтров на скачках передаточных функций операторов возникает явление Гиббса. Может ли значение амплитуды выбросов явления Гиббса превышать 10% от величины скачка передаточной функции? 2- нет.
ВОПРОС 3.1.14/к2. При усечении операторов идеальных высокочастотных фильтров на скачках передаточных функций операторов возникает явление Гиббса. Может ли значение амплитуды выбросов явления Гиббса превышать 10% от величины скачка передаточной функции? 2- нет.
______________________________________
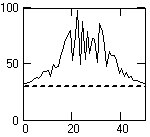
ВОПРОС 3.1.15/к3. Функция представлена кривой на рисунке. Проведена дискретизация функции, перевод в частотную область и произвольная обработка (например, сглаживание). Проявит ли себя явление Гиббса при обратном восстановлении непрерывной функции из ее частотного представления? 2- нет.
___________________________________
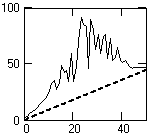
ВОПРОС 3.1.16/к4. Функция представлена кривой на рисунке. Проведена дискретизация функции, перевод в частотную область и произвольная обработка (например, сглаживание). Проявит ли себя явление Гиббса при обратном восстановлении непрерывной функции из ее частотного представления? 2- да, на обеих концах функции появятся пульсации. 2- да, но только на правом конце функции ???????????????????????????????