1.6. Кодирование

Кодирование — процесс преобразования дискретных сообщений в дискретные сиг­налы в виде кодовых комбинаций символов, составленных по определенному закону. Кодирование нашло широкое применение в современных системах передачи информа­ции для зашиты ее от помех.

Код — это закон или правило, по которому осуществляется кодирование. Кодовые комбинации составляются из символов, заданная совокупность которых называется алфавитом, а закон, по которому составляются эти комбинации, называется языком сообщений. Например, в обыденной жизни сообщение может быть составлено на рус­ском, английском, немецком или другом языке и записано с помощью русского, ла­тинского или другого алфавита. Кодовые комбинации могут быть записаны буквами, цифрами либо другими символами.

Числовые коды. В технике широкое применение нашли коды, построенные на осно­ве систем счисления. Количество символов или цифр системы называется основанием кода т системы счисления. По основанию кода т системы счисления бывают двоичные (т — 2), троичные (т = 3) и т.д. В широко применяемой десятичной системе т = 10. В ней используются цифры от 0 до 9. В двоичной системе имеется только две цифры 0 и 1. Число символов, образующих кодовую комбинацию, называется длиной кода п. Место цифры в кодовой комбинации называется разрядом. Значение (вес) разряда определяет­ся основанием т и порядковым номером разряда. В десятичной системе в первом разряде (крайнем правом) содержатся единицы, во втором — десятки, в третьем — сотни и т.д. В двоичной системе первый разряд также содержит единицы, второй — двойки, третий — четверки, четвертый— восьмерки и т.д. Таким образом вес цифры при переводе ее из одного разряда в другой более высокий увеличивается в т раз (см. табл. 1.2).

Ряд десятичных и соответствующих им двоичных чисел Таблица 1.2

	Число		Число
Десятичное	Двоичное четырехразрядное	Десятичное	Двоичное четырехразрядное
0	0000	8	1000
1	0001	9	1001
2	0010	10	1010
3	0011	11	1011
4	0100	12	1100
5	0101	13	1101
6	ОНО	14	1110
7	out	15 *	1111

При кодировании каждому сообщению присваивается определенная комбинация числового кода. Так, сообщения о состоянии четырех выключателей на контролируе­мом пункте были рассмотрены в табл. 1.1.

При передаче по каналу связи каждому символу соответствует свой сигнальный признак. Например, при двоичном коде цифре 1 соответствует импульс, а цифре 0 — пауза. Можно цифру 1 передавать длинным импульсом, а цифру 0 — коротким или передавать эти символы разными частотами (табл. 1.3).

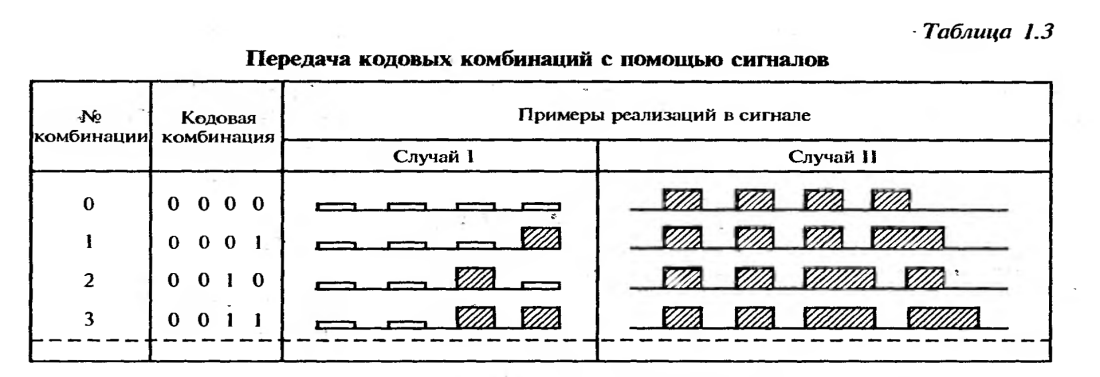
При десятичном коде должно быть десять состояний сигнала, например, десять сигнальных частот.

Полное число сигналов, образуемых числовым кодом, определяется выражением

N = т^п, (1.19)

где т — основание системы счисления; п — число разрядов (элементов сигнала).

Наиболее широкое применение в технике нашел двоичный код, так как он соот­ветствует двоичной природе многих сообщений («да-нет», «включено-отключено»). Операции с двоичными числами достаточно просты. Выражение (1.19), определяющее полное число возможных сигналов, принимает вид N= 2^п.

Кроме простых числовых кодов применяются составные, имеющие два основания и более. Наибольшее распространение из них получили единично-десятичные и двоич­но-десятичные коды.

Единично-десятичный код характеризуется тем, что каждая цифра десятичного числа записывается одними единицами. Например, число 325 запишется как 111-11-11111. В двоично-десятичном коде каждая цифра десятичного числа от 0 до 9 записывается четы­рехразрядным двоичным кодом. Такой код позволяет образовать N—2⁴ =16 различных комбинаций, десять из которых могут быть использованы для обозначения десяти цифр десятичной системы. Наибольшее применение нашел код, в котором десятичная цифра представлена ее точным двоичным числом. Такой код иногда обозначают 8 - 4 - 2 -1 по весу двоичных цифр в каждом разряде. Например, число 325 в двоично-десятичном коде имеет следующий вид: 0011-0010-0101. Передача разделительных знаков между че­тырехразрядными группами (тетрадами) не обязательна, так как каждый разряд содер­жит одинаковое число символов, равное 4.

По числу элементов в кодовых комбинациях коды делятся на равномерные (ком­плектные) и неравномерные (некомплектные). Кодовые комбинации комплектных ко­дов имеют одинаковую длину (число символов в коде), некомплектных — разную. Комплектность кода позволяет несколько повысить его помехоустойчивость, так как при этом возможно контролировать число элементов в кодовых комбинациях. Так, число 325 в комплектном единично-десятичном коде записывается в следующем виде: 0000000111-0000000011-0000011111.

По наличию избыточности коды делятся на избыточные (помехоустойчивые) и неизбыточные (непомехоустойчивые). К последним относятся все коды, в которых заме­на в комбинации одного символа другим (например, 1 на 0 или 0 на 1) приводит к ошибке. Числовые коды, в которых используются все возможные комбинации (коды на все сочетания), являются непомехоустойчивыми. Искажение хотя бы одного символа в передаваемой комбинации приводит к появлению новой комбинации, соответствую­щей другому сообщению. Однако, несмотря на низкую помехоустойчивость, эти коды широко применяют в тех случаях, когда влияние помех при передаче несущественно.

Комбинаторные коды основаны на математической теории соединений: перестано­вок, размещений и сочетаний.

Коды, построенные по закону перестановок, содержат п символов в каждой ком­бинации. Отдельные комбинации отличаются друг от друга только порядком следова­ния символов. Общее число возможных комбинаций определяется выражением

N = Р_п =1x2x3 х...х п = n !, (1.20)

где Р_п — число перестановок.

Коды, построенные по закону размещений, представляют собой комбинации из п элементов по т символов, отличающихся символами или порядком их следования. Число возможных комбинаций определяется выражением:

(1,21)

Например, имеем п - 3 (а, б, в) и т = 2, тогда число возможных комбинаций:

(аб, ба, ав, ва, бв, вб).

Коды, построенные по закону сочетаний, представляют собой комбинации по т символов из п возможных, отличающиеся только символами. Число возможных комби­наций определяется выражением:

(1,22)

Например, имеем п = 4 (а, б, в, г) и т = 2, тогда число возможных комбинаций 4x3

(аб, ав, аг, бв, бг, вг). Такие коды называют кодами на одно сочетание.

Код типа С¹_n при временном разделении элементов сигналов называют распределительным.

Кодом на все сочетания называют код, составленный из заданного числа элемен­тов п и представляющий суммарную комбинацию сочетания:

(1,23)

Помехозащищенные коды. Рассмотренные выше простые числовые коды при осно­вании системы счисления т и числе разрядов n₀ позволяет образовать N₀ = т возмож­ных комбинаций. Отсюда минимальная длина кодовой комбинации, необходимая для образования всех N₀ комбинаций,

(1,24)

Такой код называют минимальным или безызбыточным. В нем некоторые комбина­ции могут отличаться друг от друга не более, чем в одном элементе. Для оценки помехо­защищенности кода от воздействия помех вводят понятие кодового растояния d — числа разрядов, в которых элементы одной кодовой комбинации отличаются от другой. Так, комбинация 0000 и 0001 отличаются только в одном разряде (d = 1). Это означает, что появление 1 в первом разряде комбинации 0000 или 0 в первом разряде комбинациии

• приводит к изменению передаваемого сообщения. Для того, чтобы избежать ошиб­ки в случае одиночных искажений, нужно увеличить кодовое расстояние до d = 2, исключив комбинации только в одном разряде (элементе).

Кодовое расстояние, обозначаемое буквой d, определяется путем сложения двух комбинаций по модулю 2 (mod 2), которое обозначается знаком ® и производится в соответствии с табл. 1.4.

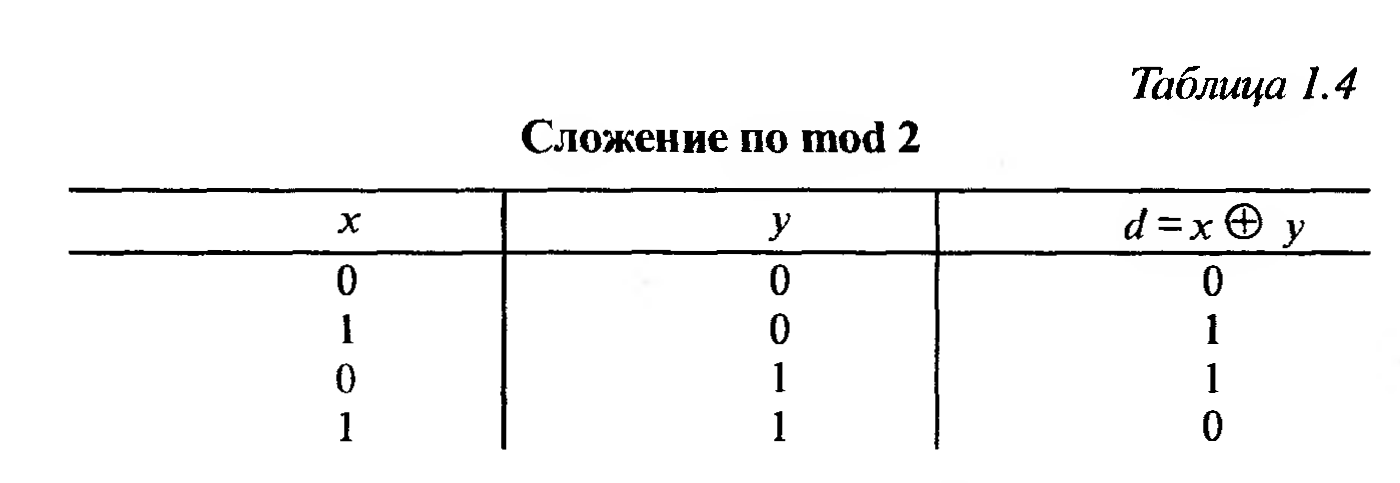
При суммировании по mod 2 двух комбинаций нули будут в тех разрядах, где символы в обеих комбинациях одинаковы, а единицы — где символы различны. Напри­мер, сложение по mod 2 двух пятиразрядных чисел дает следующий результат:

Отсюда d =3.

Для того, чтобы определить кодовое расстояние между различными кодовыми комбинациями, составляют матрицы (табл.1.5).

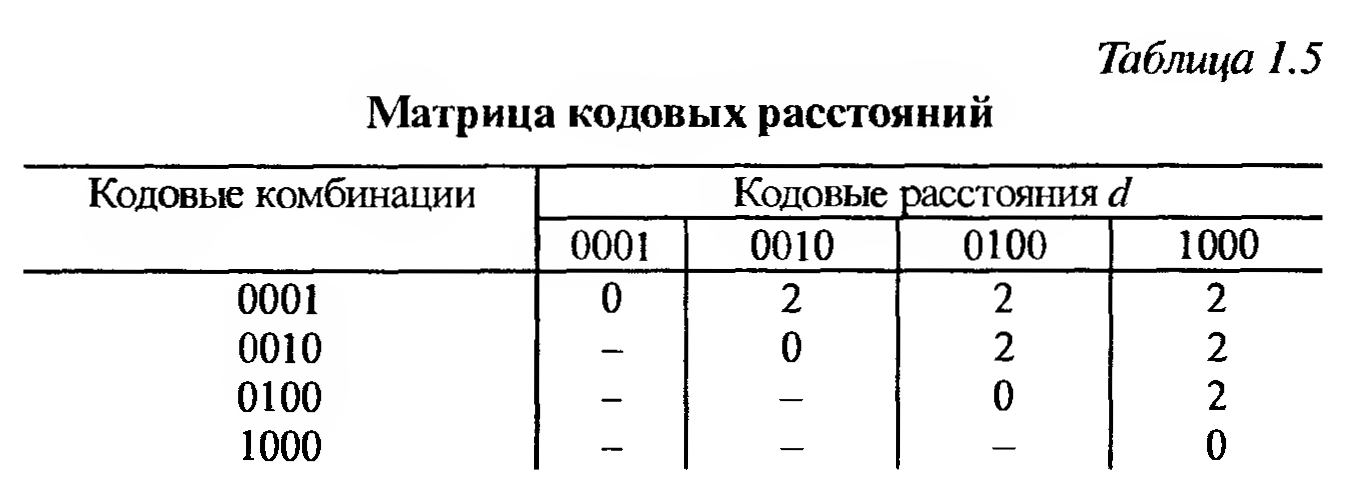
Нетрудно убедиться, что при любом одиночном искажении комбинации, приве­денные в табл. 1.5, не могут переходить одна в другую. Следовательно, при одиночном искажении произойдет появление новой комбинации, по которой можно судить об искажении. Двойные искажения при d_min= 2 обнаружить нельзя. Для получения еще большей помехоустойчивости необходимо увеличить кодовое расстояние. Так, при d_min= 3 можно обнаружить любые двойные, а при d_min= 4 — тройные искажения.

В общем случае получим выражение:

(1,25)

где r_об — количество ошибок, которое можно обнаружить.

Для построения помехозащищенного кода необходимо разбить все комбинации на две группы: разрешенные (основные) с кодовым расстоянием d_min > r_об +1; запре­щенные с кодовым расстоянием d_min ≤ r_об.

Помехозащищенным кодом можно передать меньшее число сообщений, чем ко­дом, в котором используются все комбинации при одинаковом числе элементов в ко­дах. При одинаковом числе сообщений в комбинациях помехозащищенного кода при­ходится затрачивать большее число элементов. Такие коды имеют избыточность, кото­рую оценивают коэффициентом избыточности:

(1,26)

где п — число элементов в комбинациях кода с избыточностью; n₀ - число элементов в комбинациях неизбыточного кода.

При кодовом расстоянии d_min > 2 можно не только обнаружить, но и исправить ошибку. Рассмотрим две кодовые комбинации 0011 и 1000, отличающиеся тремя эле­ментами. Допустим, при передаче комбинации 1000 произошло одиночное искажение, получим 0000 1100 1010 или 1001. Можно с уверенностью сказать, что была передана комбинация 1000, т.е. исправить ошибку. Чтобы исправить любое число ошибок r_и, минимальное кодовое расстояние нужно определить по формуле:

(1,27)

Отсюда для исправления одиночной ошибки (r_и — 1) d_mm = 3.

Способность кода обнаруживать и-исправлять ошибки определяется минималь­ным кодовым расстоянием из выражения:

(1,28)

где r_о6 и r_н — число обнаруженных и исправленных ошибок при условии r_об > r_и.

Среди помехозащищенных кодов различают блочные и непрерывные. К блочным кодам относятся такие, с помощью которых сообщения передаются блоками опреде­ленной длины из некоторого конечного числа символов.

В непрерывных кодах нет последовательности информационных символов опреде­ленной длины. Между информационными символами по определенному закону разме­щают проверочные. Для декодирования таких кодов обычно применяют ЭВМ. В систе­мах телемеханики обычйо применяют блочные коды. Их делят на систематические (ли­нейные) и несистематические (нелинейные).

К систематическим относят коды, у которых сумма по mod 2 двух разрешенных комбинаций является комбинацией того же кода. Несистематические коды образуются с помощью нелинейных операций над информационными символами. К несистематичес­ким кодам относится, например, корреляционный код, в котором единица передается символом 10, а нуль — 01. Например, если комбинация в исходном неизбыточном коде имеет вид 1011, то в корреляционном она будет записана как 10 01 1010. Если в таком коде появляется подряд три нуля или единицы, то это свидетельствует об ошибке.

Коды с повторением предусматривают повторение каждой комбинации 2 раза и более. Такие коды могут бьггь двух вариантов: код с защитным повторением без инвер­сии и с инверсией. Код с повторением и инверсией более целесообразно применять при несимметричном канале связи, в котором чаще появляются ошибки одного знака.

Для повышения достоверности передачи кодированной информации кроме поме­хозащищенных кодов применяют также обратную связь (обратный канал) и мажори­тарное декодирование. В системах с информационной обратной связью приемник, при­няв сообщение, передает его же по обратному каналу. Передающее устройство сравни­вает переданное им сообщение с полученным по каналу обратной связи. При совпаде­нии сообщений передается разрешающий сигнал, при несовпадении — сигнал запрета. В таких системах используют обычно двоичный безызбыточный код.

При мажоритарном декодировании в канал связи передается не менее трех оди­наковых кодовых комбинаций. Решение о правильности принимается по большинству одинаковых принятых комбинаций («метод голосования»).

Известен ряд других методов повышения достоверности передачи, основан­ных'на внесении той или иной избыточности как при посимвольном приеме кодо­вых комбинаций (определяется достоверность приема каждого отдельного символа по Ходу передачи), так й при приеме кодовых комбинаций в целом с последую­щим определением их правильности.