1.3. Информация в системах управления электроснабжением железных дорог

Общие понятия и определения. Во всех автоматических устройствах, системах теле­механики, вычислительных машинах от одних частей и узлов к другим осуществляется передача сведений о происходящих в них процессах и явлениях, т.е. информации.

Информация представляет собой сведения, содержащиеся в сообщении, заранее неизвестные получателю.

Сообщение — это сведения о некотором событии или явлении, которые необходи­мо передать от источника сообщений к получателю сообщений. Сообщения передаются с помощью сигналов по каналам связи.

Сигнал — физический процесс, определенные параметры которого соответствуют некоторому сообщению. Сигнал всегда порождается некоторым фактом, событием или явлением и имеет независимую от него физическую природу. Между сигналом и сооб­щением существует условное соответствие, как между деталью и ее чертежом.

Сигналы существуют в пространстве и во времени независимо от тех событий, которыми они были порождены. Читая книги, рассматривая фотографии, получая информацию по радио и телевидению, мы узнаем о событиях, давно прошедших или происходящих сейчас (прямое включение с места событий) рядом с нами или на значительном расстоянии.

В процессе передачи и приема сигнала осуществляются его многократные преоб­разования из одной формы в другую. Например, принимаемый радиосигнал преобразу­ется в электрический, который в свою очередь — в звуковой или световой. При переда­че сигналов происходит обратное преобразование.

Сигналы могут взаимодействовать друг с другом, образуя новые сигналы и сооб­щения, причем смысл нового сообщения будет отличен от смысла сообщения каждого из взаимодействующих сигналов.

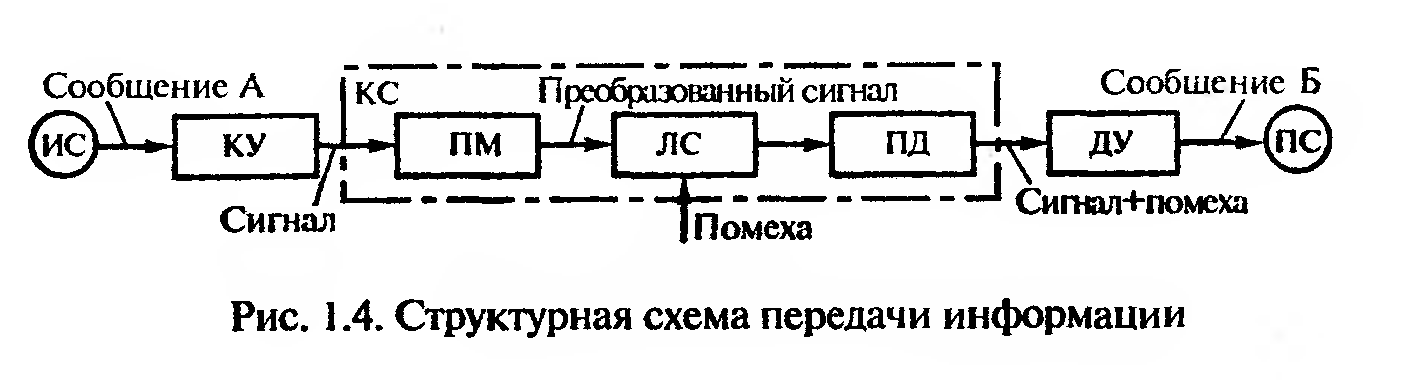
Система передачи информации (рис. 1.4) состоит из источника сообщения (ИС), кодирующего устройства (КУ), преобразующего сигнал в вид, удобный для передачи по каналу связи (КС), состоящему из передатчика — модулятора (ПМ), линии связи (JIC), приемника-демодулятора (ПД), преобразующего сигнал в пер­воначальный вид, декодирующего устройства (ДУ), преобразующего сигнал в сооб­щение, получателя сообщений (ПС).

Канал связи представляет собой совокупность технических средств, с помощью ко­торых обеспечивается независимая передача различных сообщений по одной линии свя­зи. В процессе передачи сигнала по каналу связи на него могут воздействовать помехи.

Помеха — это любое мешающее воздействие, возникающее в процессе передачи сигнала. Различают аппаратные помехи и помехи от внешних воздействий. Помехи мо­гут частично или полностью исказить передаваемое сообщение А в сообщение Б, при­нятое получателем ПС. За­дача передачи информа­ции по каналу связи бу­дет выполнена, если сооб­щение Б, принятое ПС, точно соответствует пере­данному сообщению А.

По своему характеру информация, передаваемая в системах управления устрой­ствами электроснабжения, может рассматриваться как оперативная, предназначенная для постоянного контроля за состоянием системы электроснабжения и непосредствен­ного управления ею с диспетчерского пункта; статистическая, предназначенная для обработки, обобщения и анализа результатов эксплуатации системы электроснабже­ния, планирования и нормирования производственных процессов; отчетная, исполь­зуемая для составления отчетных документов.

По назначению информация в системе электроснабжения делится на распоряди­тельную (об управлении и регулировании режимов работы электроустановок); сигналь­ную (о положении и состоянии контролируемых объектов); измерительную (о величине контролируемых параметров).

Количество сообщений и количество информации. Каждое событие или явление мо­жет иметь N различных состояний. Сигнал, описывающий это событие, должен также иметь N состояний. Пусть требуется передавать на диспетчерский пункт информацию о состоянии четырех (п = 4) выключателей на контролируемом пункте. Каждый выклю­чатель имеет два состояния: «включен» и «отключен» (т = 2). Обозначим отключенное состояние выключателя «О», включенное — «1» и запишем все возможные сообщения о состоянии четырех выключателей.

Таблица 1.1

Сообщения о состоянии выключателей

Номер сооб­ щения	Состояние выключателей					Номер сообще­ ния		Состояние выключателей
	1	2	3	4	1			2	3	4
1	0	0	0	0	9		1		0	0	0
2	0	0	0	1	10		1		0	0	1
3	0	0	1	0	11		1		0	1	0
4	0	0	1	1	12		1		0	1	1
5	0	1	0	0	13		1		1	0	0
6	0	1	0	1	14		1		1	0	1
7	0	1	1	0	15		1		1	1	0
8	0	1	1	1	16		1		1	1	1

В табл. 1.1 перечислены все возможные сообщения о состоянии четырех выключате­лей от первого (все выключатели отключены) до шестнадцатого (все выключатели вклю­чены). Нетрудно убедиться, что между числом сообщений (N= 16), количеством объек­тов (и = 4) и числом их состояний (т = 2) существует зависимость 16 — 2⁴, которую можно при произвольных тип записать как

N=m. (1.1)

Число возможных сообщений является некоторой мерой информации. Однако пользоваться этой мерой неудобно, так как существует степенная зависимость между количеством сообщений и числом объектов, о которых необходимо передавать эти со­общения. В системе телеуправления «Лисна-Ч» можно передавать сообщения о 126 объек­тах тяговых подстанций (п = 126). Количество сообщений, которое при этом может быть передано (N = 2¹²⁶), определяется числом 10³⁸.

Для измерения информации более удобна логарифмическая мера, которая позво­ляет получить линейную зависимость между количеством информации и числом объек­тов или числом элементов в сигнале, с помощью которого передается информация:

I = log_e N = пlog,, т, (1.2)

где а — основание логарифма, может быть любым, но более удобно принять а = 2.

При т = 2 выражение (1.2) можно записать

I =log₂ N = nlog₂ 2 = п. (1.3)

За единицу количества информации принимают информацию, содержащуюся в сообщении об объекте, имеющем два состояния. Сигнал, который описывает данное событие, имеет также два состояния. Единица количества информации носит название бит от сокращения английских слов (двоичная единица).

Таким образом, если двоичный сигнал состоит из одного элемента, он несет один бит информации и с его помощью может быть передано только два сообщения типа «да-нет» (включено-отключено, 1-0)

Выражение (1.2) определяет наибольшее количество информации, которое мо­жет содержаться в передаваемом сигнале. Фактическое значение количества информа­ции / может быть значительно меньшим.

При прохождении сигналов по каналам связи передаются определенные сооб­щения. В них кроме полезных могут быть заранее известные или бессмысленные сведе­ния. Истинное значение информации в сообщении определяется лишь полезными сведениями.Разница между истинным и наибольшим значением информации пред­ставляет собой избыточную информацию. Уменьшая избыточную информацию в ре­альных сообщениях, можно канал связи использовать более эффективно. Повседнев­но мы осуществляем сокращение избыточной информации, не думая о понятии «ин­формация». Например, посылая поздравительную телеграмму, мы опускаем в тексте знаки препинания, предлоги, отдельные слова, имея в виду, что получателю и так будет понятен смысл сообщения.

Однако в ряде случаев избыточная информация может быть полезной, помогая вос­станавливать информацию при ее искажении помехой. Для повышения гарантии получе­ния переданной информации без потерь нередко передают избыточную информацию. Так, например, в телеуправлении команда «Включить»-«Отключить» передается два раза, пол­ное совпадение двух кодовых серий гарантирует отсутствие искажений команды.

Непрерывные и дискретные сигналы. Сигналы как и сообщения бывают непрерыв­ные и дискретные. Непрерывные сигналы могут отличаться друг от друга на очень малую величину. Дискретные сигналы представляют собой позиционные команды «Включить- Отключить», «Открыть-Закрыть» и т.п. Непрерывные сигналы используются в системах телеизмерения, а дискретные — в устройствах телеуправления и телесигнализации.

Типичным примером дискретных сообщений и сигналов является передача ин­формации о состоянии выключателей на подстанции. Сигнал при этом состоит из им­пульсов, параметры которых, соответствующие включенному состоянию выключате­лей, существенно отличаются от параметров импульсов, несущих информацию об от­ключенном состоянии выключателей. Между этими двумя значениями сигнал, как и само состояние выключателей, промежуточных значений не имеет (невозможно пред­ставить, что выключатель включен или отключен частично).

Передача дискретных сигналов имеет ряд преимуществ перед передачей непрерыв­ных сигналов. Чтобы передать непрерывное сообщение, представленное непрерывной функцией времени X(i), ее разбивают на ряд дискретных значений. Замену непрерывного сообщения дискретным называют квантованием (дискретизацией). Квантование сигнала осуществляют либо по амплитуде, либо по времени. Замена непрерывного сигнала диск­ретным приводит к дополнительной погрешности. Однако это не существенно, если она не велика по сравнению с погрешностями, вызванными другими причинами.

На рис. 1.5 представлено квантование сигнала по амплитуде. При квантовании по амплитуде кривую X(t) разбивают на равные интервалы АХ по вертикали и заменяют ступенчатой характеристикой X'(t) Интервал АХ называют шагом квантования. При за­данном шаге квантования число дискретных значений сигнала (разрешенных уровней) в пределах изменения функции X{t) от Х_тах до X_min равно:

(1.4)

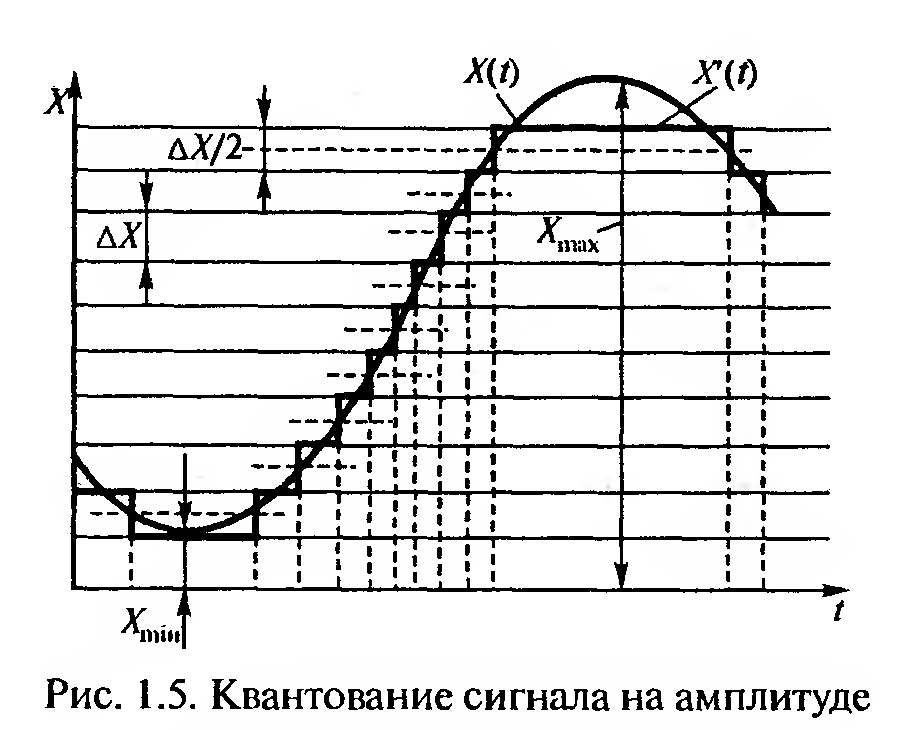
Если мгновенное значение функции по­падает внутрь интервала, то оно заменяется бли­жайшим разрешенным. Переход с одного уров­ня на другой происходит в момент, когда зна­чение функции находится в середине интерва­ла квантования, так как именно в этот момент абсолютная погрешность квантования оказыва­ется наибольшей.

Погрешность квантования определяется выражением

(1.5)

Из выражений (1.4) и (1.5) видно, что с уменьшением АХ и увеличением N по­грешность уменьшается.

При квантовании по времени кривую X(t) разбивают на равные интервалы по горизонтали и передают только те значения сигнала, которые совпадают с началом (или концом) каждого интервала. Следовательно, при квантовании по времени переда­ча сигналов происходит в определенные фиксированные моменты времени.

Теоретически скорость передачи информации по каналу связи, определяющая пропускную способность канала, может быть выражена формулой

(1.6)

где ∆F_K — ширина полосы канала связи (полоса частот, которую пропускает канал);

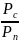— отношение мощности сигнала к мощности помехи.

" Если в секунду передается с бит информации, то за время работы канала связи Т_к можно передать количество информации

(1.7)

Мощность сигнала Р_с не может быть больше мощности Р_к, допустимой в канале. Приняв Р_с= Р_к, получим выражение, определяющее наибольшее количество инфор­мации в канале:

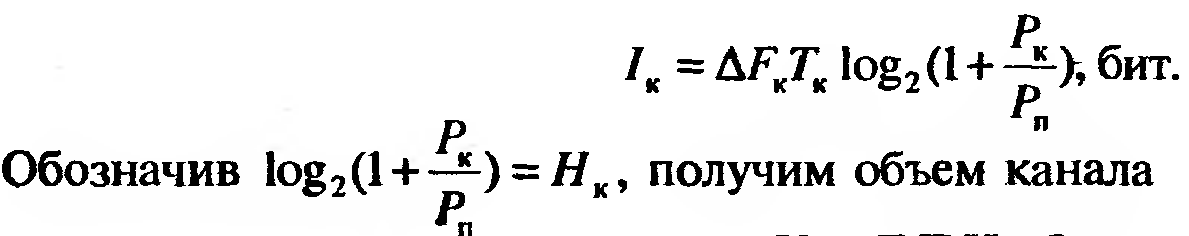(1.8)

(1.9)

где Н_к — динамический диапазон канала связи.

По аналогии можно записать выражение объема сигнала:

(1.10)

где F_c — ширина полосы частотного спектра сигнала; Т_с — длительность сигнала; Н_с — динамический диапазон сигнала

Необходимым условием передачи сигнала по каналу связи является У_к > У_с, но при этом должны быть выполнены и достаточные условия: F_K > F_c; Т_к > Т_с; В_к > Н_с.

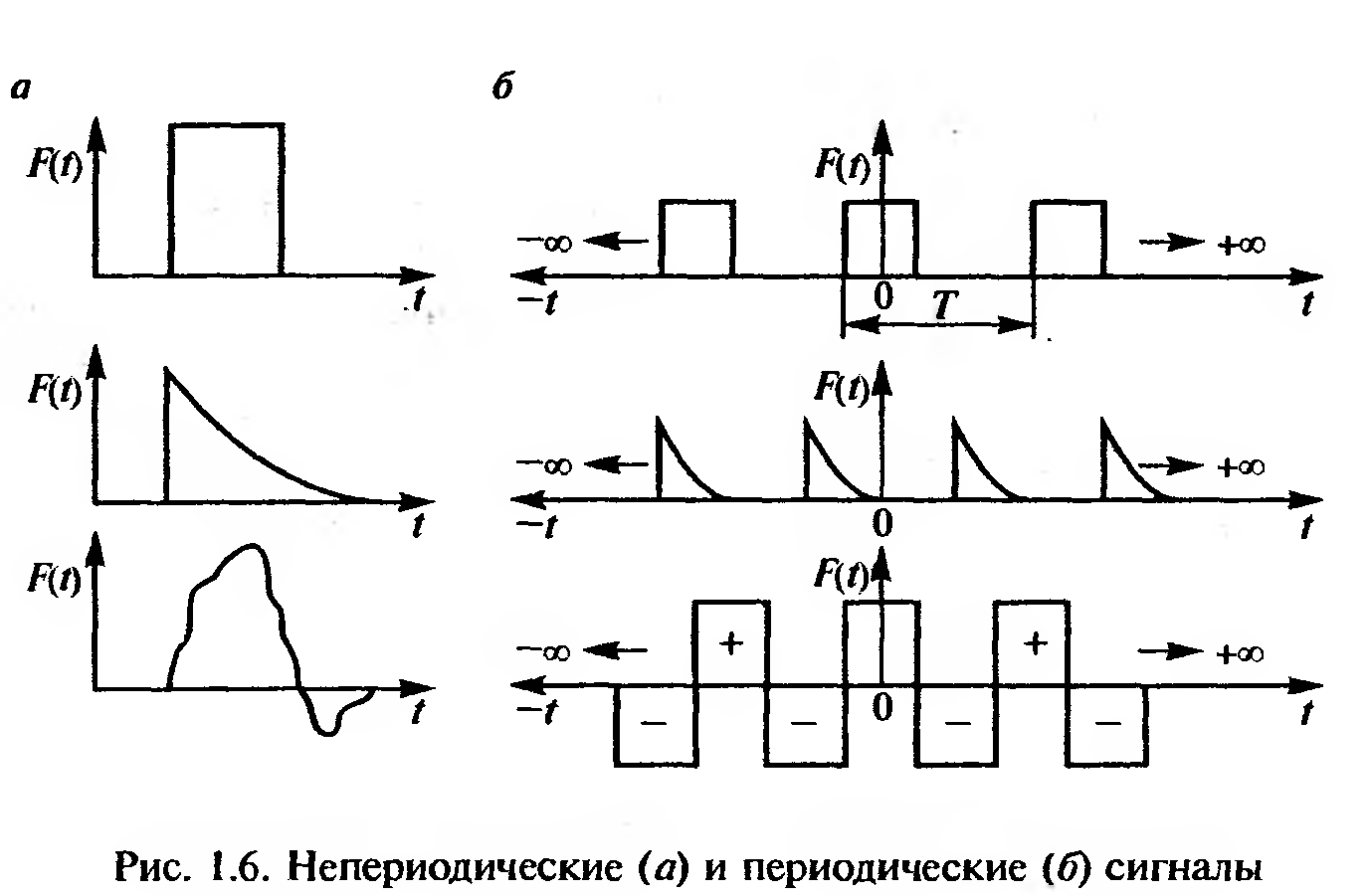
Сигналы и их спектры. Телемеханические сигналы, передаваемые по проводным линиям и радиоканалам, представляют собой электрическую величину, изменяющую­ся во времени.В последние годы начинают широко применяться оптические сигналы, передаваемые по волоконно-оптическим кабелям. Различают сигналы непериодические и периоди­ческие. Первые являются не­периодической функцией времени, в простейшем слу­чае — это одиночные им­пульсы произвольной формы (рис. 1.6, а). Вторые являются периодической функцией времени и представляют со­бой бесконечную времен­ную последовательность импульсов с одинаковой формой и периодом повто­рения Т (рис. 1.6, б).

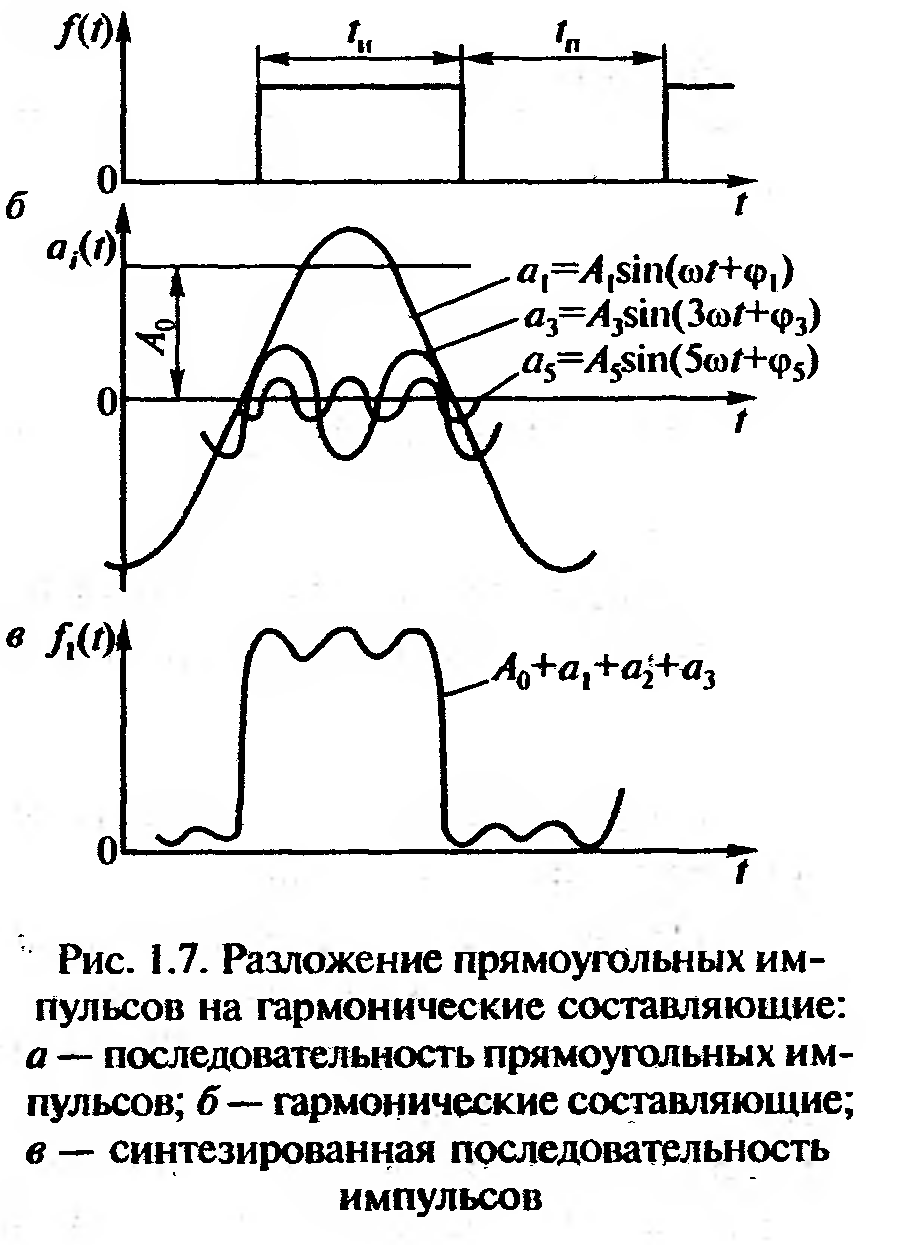
Любая периодическая

функция времени F[t) может быть представлена в виде суммы ряда синусоидальных коле­баний (ряда Фурье) с определенными амплитудами A_r начальными фазами ᵠ_i;- и частота­ми со. Следовательно, любой периодический сигнал можно представить в виде ряда

(1.11)

где —A₀ постоянная составляющая (амплитуда нулевой гармоники);A₁, А₂, А₃— амплиту­да соответственно гармоник 1,2,3; ω = 2πf — угловая частота первой гармоники; f = 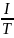— частота первой гармоники в Гц; Т— период повторения импульсов, с.

На рис. 1.7 представлен результат процесса разложения прямоугольных импульсов (рис. 1.7, а) на гармонические составляющие (рис. 1.7, б). Так как амплитуда гармоник, номера которых кратны отношению 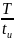при t_и ≤ t_п или 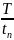при t_п ≤ t_и обращаются в нуль, то при t_и = t_п 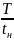2 т.е. гармоники, номера кото-

рых кратны 2 (четные), обращаются в нуль. По этой причине на рис. 1.7, б отсутствуют четные гармоники. Амплитуда гармоник по мере возрас­тания частоты (номера) снижаются. На рис. 1.7, в показана последовательность, полученная в ре­зультате сложения нулевой A₀, первой, третьей и пятой гармоник. Кривая наглядно показывает, что чем больше гармоник суммируется, тем бли­же синтезированная последовательность совпадает с исходной (рис. 1.7, а).

Чтобы при передаче сигнала, состоящего из последовательности прямоугольных импульсов, не произошло искажений, нужно передать по кана­лу весь бесконечный ряд гармоник в соответствии с выражением (1.11). Практически осуществить это невозможно, так как потребовался бы канал с бесконечной полосой пропускания. Обычно до­пустимы некоторые искажения формы сигнала, что позволяет ограничиться передачей конечного числа гармонических составляющих.

Амплитуды гармонических составляют , графически представляются в координатах А_к и в виде отдельных спектральных линий (где к номер гармоники). Совокупность амплитуд А_к гар­монических составляющих представляет собой спектр амплитуд, который называют линейчатым, т.к. он состоит из отдельных спектральных линий.

На рис. 1.8 приведены спектры амплитуд последовательностей прямоугольных импульсов оди­наковой длительности, но с различными перио­дами Т. Амплитуды гармоник с частотами, крат­ными 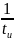, обращаются в нуль, т.к. номер первой гармоники с нулевой амплитудо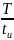й (или 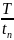), а её частота

Если нет специальных оговорок относитель­но величины искажения импульсов при переда­че, то достаточно ограничиться передачей только тех гармоник, частоты которых лежат между на­чалом координат и частотой первой гармоники из числа тех, амплитуды которых равны нулю (пер­вый «лепесток» спектра).

В этом случае ширина спектра сигнала или

необходимая для передачи полоса канала связи определяется выражением.

(1,12)

Из приведенных формул видно, что полоса пропускания канала связи обратно про­порциональна длительности наиболее короткого элемента сигнала (импульса или паузы).

Непериодические сигналы можно рассматривать как периодические с периодом повторения, равным бесконечности. На рис. 1.8 приведены спектры периодической пос­ледовательности прямоугольных импульсов одинаковой амплитуды и длительности, но с разными периодами повторения. Из приведенных спектров видно, что при увеличе­нии периода Т частотное расстояние между спектральны­ми линиями уменьшается, а количество линий увеличива­ется. Нетрудно представить, что при увеличении периода до бесконечности спектральные линии сближаются настоль­ко, что сливаются между собой, а их число увеличивается до бесконечности на любом конечном интервале частот. В этом случае нет необходимости говорить об отдельных гар­монических составляющих сигнала, и поэтому вводят по­нятие спектральной плотности S(f) как функции частоты. График спектральной плотности одиночного прямоуголь­ного импульса показывает, что огибающая кривая обращается в нуль при частотах: 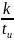, где к — 1, 2, 3 и т.д.

Для передачи сигнала используют предельно малую ширину спектра, но такую, чтобы в ней была сосредоточе­на основная энергия сигнала. Из рис. 1.9 видно, что наибольшая энергия сигнала сосредоточена в пределах первого «лепестка» спектра. Отсюда необходимая для передачи полоса канала связи определяется выражением:

∆f= (1,13)

Для передачи информации по каналу связи необходимо иметь переносчик сигна­лов, в качестве которого может быть использован любой физический процесс, способ­ный распространяться в пространстве. Переносчиками информации могут быть, на­пример, звуковые волны, свет и т.д. В автоматизированных системах в качестве пере­носчика сигналов используют электрический ток, способный практически мгновенно распространяться по проводам на большое расстояние. Для нанесения сигнала на пере­носчик (электрический ток) необходимо воздействовать на параметры переносчика с целью их изменения во времени по заданному закону.

Модуляция — процесс нанесения информации на переносчик, а параметры пере­носчика, на которые воздействуют при нанесении информации, называются качества­ми (признаками) электрического тока.

В качестве переносчика информации может быть использован постоянный ток, переменный синусоидальный ток или периодическая последовательность импульсов. При модуляции постоянного тока можно воздействовать на его амплитуду (тока или напряжения) (рис. 1.10, а). Гармонические колебания переменного тока характеризу­ются амплитудой, частотой и фазой (рис. 1.10 б, в, г), а периодическая последователь­ность импульсов — амплитудой, шириной (временем) импульсов, частотой повторе­ния, фазой и полярностью (рис. 1.10 д, е, ж, з, и).

Рис. 1.10. Признаки электрического тока: а — амплитудный при постоянном токе; б, в, г — амплитудный, час­тотный и фазовый при гармоническом колебании; д, е, ж, з, и — амплитудный, временной, частотный, фазовый и полярный при не­сущей периодической последовательности импульсов

К признакам электрического тока предъявляют следующие основные требова­ния: возможность получения большого числа состояний признака; простота образо­вания и обнаружения признака; возможность независимой передачи в одной физи­ческой среде, например, в линии связи; способность противостоять помехам и воз­действиям линии связи и аппаратуры.

Наиболее универсальным является частотный признак, который может иметь неогра­ниченное число состояний и позволяет одновременно передавать по одной линии несколько состояний. Амплитудный, признак больше подвержен действию помех, чем частотный.

Вид модуляции определяется переносчиком и его параметром (признаком), на который воздействуют при нанесении информации. При постоянном токе в качестве переносчика возможна амплитудная модуляция (AM).

Гармоническое колебание характеризуется амплитудой, частотой и фазой, и мо­жет быть описано выражением:

(1,14)

где А₀, ω₀, ᵠ₀— соответственно амплитуда, частота и начальная фаза несущего колебания.

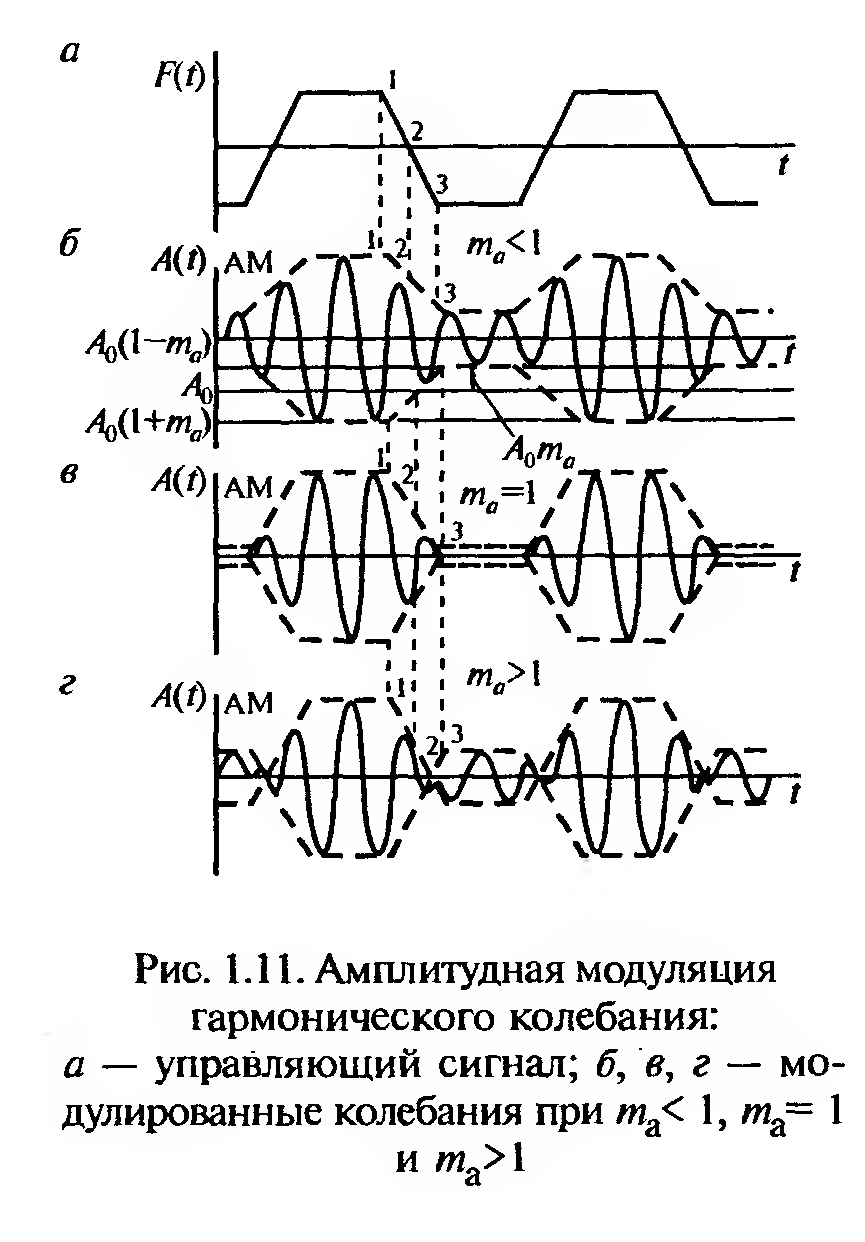
Амплитудная модуляция (AM) представлена на рис. 1.11. На рис. 1.11, а показан изменяющийся во времени сигнал F(t), который необходимо нанести на амплитуду A₀ гармонического колебания, при этом амплитуда получит некоторое приращение ∆А.

Амплитуда модулированного колебания равняется где

глубина

модуляции (рис. 1.11,6). Чтобы не произошло искажения передачи, прирашение ДА не должно быть больше A₀. При ∆А — A₀ имеем т_а= 1 (рис. 1.11, в). Дальнейшее увеличе­ние ∆А приводит к тому что т_а> 1 (рис. 1.11, г), и при этом возникают искажения. Как видно из рис.1.11, амплитуда модулированного колебания меняется во времени по закону изменения сигнала F(f), наносимого на гармоническое колебание:

(1,15)

Следовательно, модулированное колебание не является гармоническим и должно раскладываться на гармонические составляющие. Разложение АМ-колебаний в спектр

показывает, что в нем содержится несущее коле­бание с частотой ω₀, а также колебания верхних и нижних боковых частот. В простейшем случае, если модуляция осуществляется синусоидальным низ­кочастотным сигналом с частотой Ω, в спектре имеется несущее колебание с частотой ω₀ , верх­няя боковая гармоника с частотой ω₀+ Ω ниж­няя — с частотой ω₀ + Ω

Для уменьшения полосы частот широко ис­пользуют однополосную амплитудную модуляцию, при которой в канал связи передают только одну из боковых частот без несущей. Уменьшение по­лосы частот канала и повышение мощности гар­моник, несущих информацию, позволяет повы­сить помехоустойчивость.

При частотной модуляции (ЧМ) по закону меняющегося сигнала F{t) изменяется частота не­сущего колебания:

(1,16)

где ∆ω — девиация частоты, т.е. наибольшее от­клонение ее от ω₀ (обычно ∆ω<< ω₀).

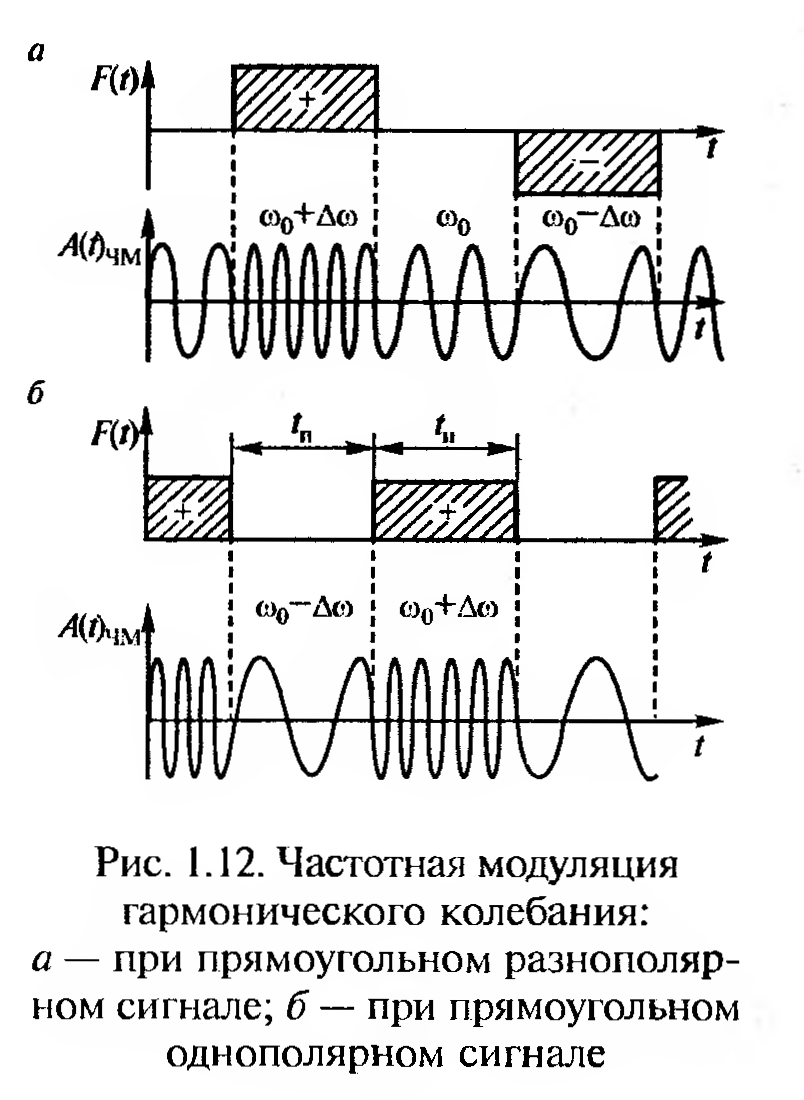
Наиболее наглядно можно представить частотную модуляцию при модулирующем сигнале в виде Последовательности разнополярных прямоугольных импульсов (рис. 1.12, а). В этом случае передаче положительного импульса соответствует частота ω₀+∆ω, передаче отрицательного импульса — частота ω₀ - ∆ω, а при паузе передается несущая частота ω₀.

При передаче однополярных импульсов (рис. 1.12, б) импульс передается частотой ω₀+∆ω, пауза — частотой ω₀—∆ω. Несущая частота при передаче отсутствует, она равна средней арифметической между частотой импульса и паузы.

Спектр ЧМ-колебания состоит из гармоник несущей частоты и боковых полос (верхней и нижней). Число гармоник в каждой боковой полосе бесконечно даже при модуляции синусоидальным сигналом (в отличии от AM, при которой в этом случае имеется по одной боковой гармонике с каждой стороны). Полоса частот при ЧМ значи­тельно шире, чем при AM, и это является недостатком ЧМ. Однако, при ЧМ обеспечи­вается существенно большая помехоустойчивость, чем при AM.

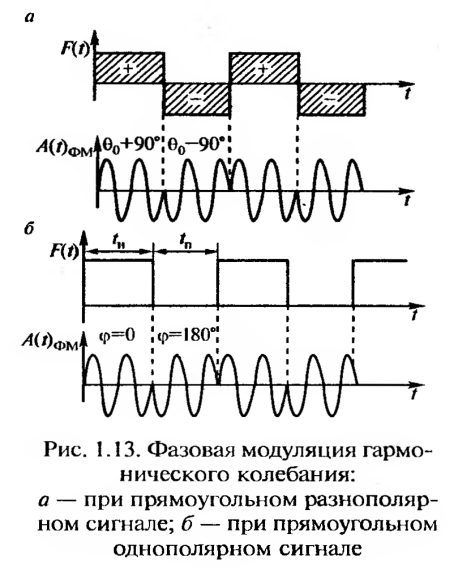
При фазовой модуляции (ФМ) по закону управляющего сигнала изменяется фаза несущего колебания. На рис. 1.13, а показана модуляция гармонического колебания разнополярным прямоугольным сигналом. Угол, на который изменяется фаза, называ­ется углом модуляции, который на рис. 1.13, а составляет 180° (от ϴ₀ +90° до ϴ_О —90°). При однополярных импульсах передаче импульса соответствует фазовый угол ᵠ = 0°, а паузе — ᵠ=180° (рис. 1.13, б)

Установлено, что при равной ширине полосы частот и скорости передачи наи­большую помехоустойчивость обеспечивает фазовая модуляция, наименьшую— ампли­тудная, частотная занимает промежуточное положение.

При импульсной модуляции в качестве несущего колебания используют периоди­ческую последовательность импульсов. По закону изменения управляющего сигнала F(t) (рис. 1.14,о) модулируют один из параметров переносчика a(t) (рис. 1.14, б).

Различают следующие виды импульсной модуляции: амплитудно-импульсную (АИМ) (рис. 1.14, в); широтно-импульсную (ШИМ) (рис. 1.14, г); частотно-импульс­ную (ЧИМ) (рис. 1.14, д); фазо-импульсную (ФИМ) (рис. 1.14, ё); полярно-импульсную (ПИМ) (на рис. 1.14 отсутствует).

Частоту следования импульсов несущего колебания f_и выбирают по теореме В.А. Ко­тельникова, согласно которой число значений п модулирующего сигнала с шириной спектра ∆F, которое надо передать за время Т, определяется формулой:

n=2∆FT (1,17)

Отсюда следует:

(1,18)

В этом случае трудно выделить сигнал из импульсно-модулированного колебания, так как наивысшая частота модулирующего и ча­стота модулируемого колебаний очень близки по величине. Поэтому частоту модулируемого колебания выбирают в 2-3 раза больше, чем следует из выражения (1.18)

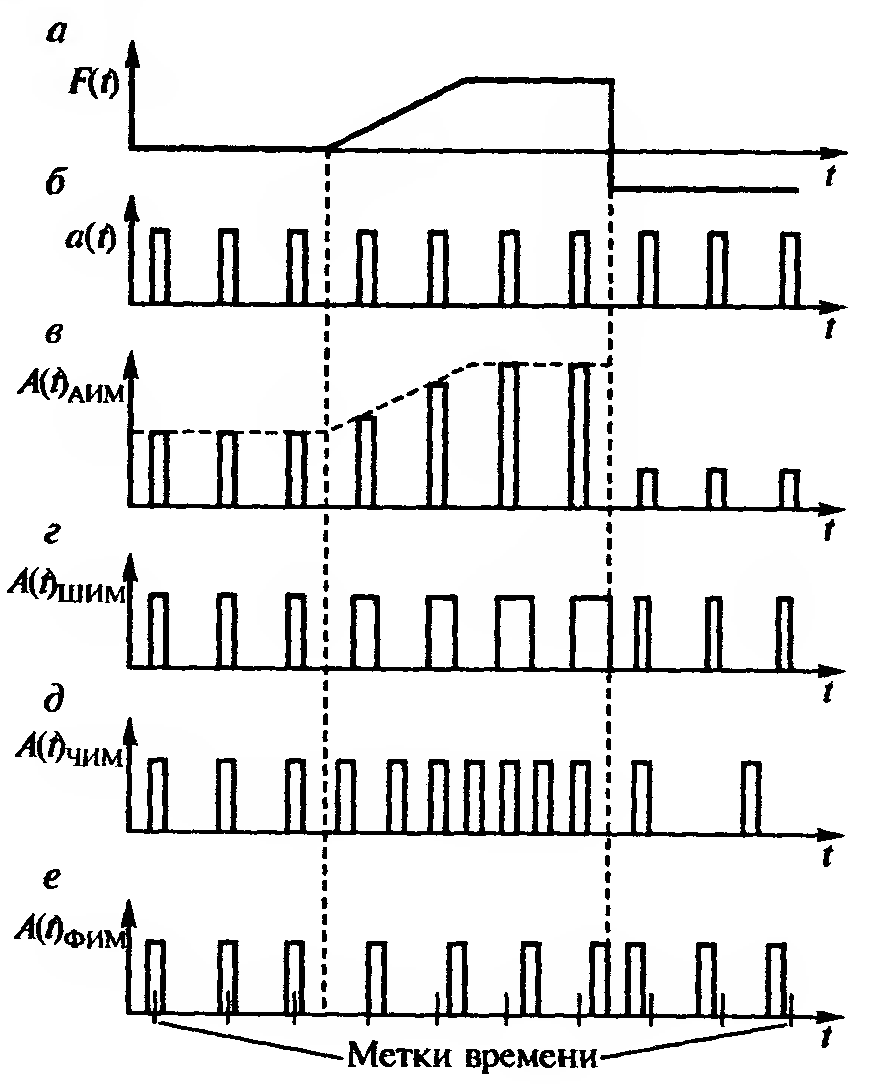
Рис. 1.14. Импульсная модуляция: а — управляющий сигнал; 6 — несущая пос­ледовательность импульсов; в, г, д, е — соот­ветственно АИМ, ШИМ, ЧИМ и ФИМ

Кроме простых видов модуляции, рас­смотренных выше, широко применяют и сложные, в которых одновременно осуществ­ляется модуляция нескольких параметров или двух различных несущих колебаний (периоди­ческая последовательность импульсов и гар­моническое колебание). Например, АИМ-АМ представляет собой модуляцию управляющим сигналом по методу АИМ периодической пос­ледовательности импульсов, а полученным сигналом модулируется по амплитуде несущее гармоническое колебание.