1. Туристские услуги:

- услуги турбюро, турагентств, бюро путешествий по бронированию и доставке путевок, оформлению документов;

- туристский отдых и путешествия по туристским маршрутам;

- туристские походы выходного дня;

- услуги для делового туризма;

- рекламно-информационные услуги туристских предприятий и организаций;

- услуги по предоставлению мест проживания;

- прочие услуги (проведение туристских мероприятий, обучение туристским навыкам; профессиональная подготовка специалистов и пр.).

2. Экскурсионные услуги:

- реализация услуг бюро экскурсий (организация индивидуальных и групповых экскурсий);

- экскурсии, которые подразделяются:

по видам – обзорные, тематические, музейные, пешеходные;

по месту проведения – городские, загородные, на маршрутах выходного дня;

по видам используемых транспортных средств – теплоходные, авиационные, автобусные и пр.

Действующий Общероссийский классификатор услуг населению не в полной мере соответствуют современным условиям рыночной экономики; ведется работа его совершенствованию и гармонизации со Статистической классификацией продукции по видам деятельности Европейского союза (ПРОДКОМ/PRODKOM).

Статистические таблицы – наиболее рациональная форма представления результатов статистической сводки и обработки статистических материалов. По форме статистическая таблица представляет собой ряд пересекающихся горизонтальных и вертикальных линий, образующих по горизонтали строки, а по вертикали – графы (столбцы, колонки). Составленная, но незаполненная таблица представляет собой макет таблицы.

По содержанию статистическая таблица имеет подлежащее и сказуемое. Подлежащее таблицы – это то, о чем говорится в таблице, представленное группами и подгруппами. Обычно подлежащее располагается в левой части таблицы.

Сказуемое таблицы – это то, что говорится о подлежащем. Это показатели, с помощью которых характеризуется изучаемое явление. Как правило, эти показатели размещают в правой части таблицы.

Оформленная таблица должна иметь общий заголовок, где изложено ее краткое содержание; единица измерения; названия строк и граф и итоги по ним.

Статистические таблицы подразделяются на: простые, групповые и комбинационные.

Простые таблицы в подлежащем содержат перечни, территориальные единицы, хронологические даты.

Групповые таблицы представляют статистические данные в сгруппированном виде, как правило, с выделением типов явления, что делает таблицу более информативной.

Комбинационные таблицы представляют собой комбинацию групп в сочетании с несколькими признаками изучаемого явления.

Подлежащие и сказуемое таблицы должны быть в тесной взаимосвязи с тем, чтобы можно было получить объективную и полную характеристику изучаемого явления.

Построение статистических таблиц предполагает соблюдение правил:

1. Таблицы должны быть наглядными и легко обозримыми;

2. Общий заголовок таблицы должен быть кратким с указанием единицы измерения, времени, территории, к которым относятся данные;

3. По строкам и графам, если это возможно, должны быть частные и общие итоги;

4. При заполнении таблиц необходимо использовать единые условные обозначения;

5. Показатели таблицы должны иметь одинаковую степень точности;

6. В таблицах значность цифр должна быть наименьшей.

Статистические графики – это наглядная, лаконичная и выразительная форма представления данных. График включает заголовок, где указывается, что представлено на графике, территория и время к которому относятся данные. Важные атрибуты графиков – условные единицы обозначения и масштаб.

По способу построения графики подразделяются на диаграммы и картодиаграммы. По графическому образу диаграммы могут быть:

- линейными;

- секторными;

- круговыми, треугольные, прямоугольные;

- столбиковые;

- ленточные;

- фигурные.

Линейные графики содержат значения показателей, соединенные отрезками прямых. Эти графики широко используются для анализа рядов распределения и временных рядов ( рис.1)

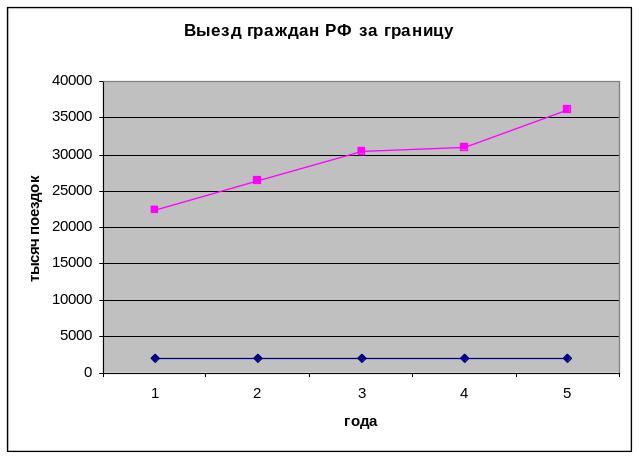
Рис. 1

Секторные диаграммы применяются для представления структуры совокупности, где вся площадь круга принимается за 100%, а сектора представляют доли составляющих частей. Например, цели поездок граждан Российской Федерации за границу ( рис.2)

Рис.2

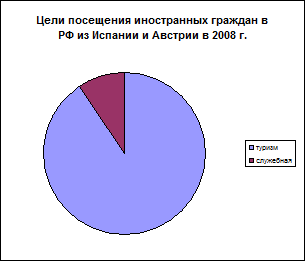
Круговые диаграммы представляют значения показателя в виде занимаемой им площади в общем объеме. Например, цели посещения иностранных граждан Российской Федерации в 2008 г. ( рис.3)

Испания						Австрия

Рис. 3

Столбиковые диаграммы используются для представления значений состава показателей (рис.4)

Рис. 4

Ленточные диаграммы решают те же задачи, что и столбиковые, но графическое изображение показателей дается в горизонтальном виде ( рис. 5)

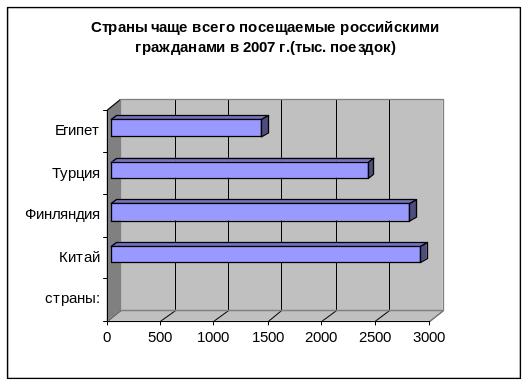
Рис. 5

Фигурные диаграммы используются для изображения изменения показателя в динамике или для пространственных сравнений.

Картодиаграммы применяют для отображения пространственных данных. Например, на карту наносятся условные обозначения, отражающие наиболее часто посещаемые туристами регионы страны.

Блок 5. Статистические ряды распределения

Результаты сводки и группировки статистического наблюдения представляются в виде статистических рядов распределения и таблиц. Статистические ряды распределения – это упорядоченное расположение единиц исследуемой совокупности на группы по группировочному признаку.

Ряды распределения делятся на вариационные и атрибутивные. Вариационный ряд – это распределение единиц совокупности по количественному признаку, а атрибутивный ряд представляет собой группировку по атрибутивным (качественным) признакам.

Вариационные ряды по способу построения бывают дискретными (прерывными) и интервальными (непрерывными). Дискретные ряды могут принимать значения целых чисел (например, число туристов в группе), а интервальные ряды объединяют признаки с непрерывным изменением (например, доходы, заработная плата, выручка от реализации и т. д.). К дискретным рядам может быть отнесено распределение семей по числу человек в них.

Число человек в семье: 2, 3, 4, 5, 6, 7 и более

% таких семей: 25 27 28 11 5 4

Вариационные ряды состоят из двух элементов – варианты и частоты. Варианта – это определенное значение варьирующего признака, а частоты – это численности отдельных вариант. Частоты, выраженные в долях единицы или в процентах к итогу, называются частостями. Например, в городе имеются различные предприятия общественного питания (табл.1).

Таблица 1

Предприятия общественного питания	Численность предприятий	В %% к итогу
Столовые Кафе Рестораны Закусочные	26 72 22 45	16 44 13 27
Итого	165	100

В данном случае численность предприятий общественного питания – это частоты, а тоже распределение выраженное в процентах – частости.

Интервальный ряд распределения может быль представлен распределением численности туристов в группах (табл. 2).

Таблица 2

Число туристов в группе (х)	% таких групп (частость) (w)	Плотность распределения ( )	Накопленная частость
До 10 11-20 21-30 31 и более	20 40 30 10	2 4 3 1	20 60 (20+40) 90 (60+30) 100 (90+10)
Итого	100,0

Характер распределения наиболее выразителен в графическом изображении. Дискретный ряд по числу человек в семье может быть представлен в виде полигона, представленного на рис. 6.

Рис. 6 Полигон распределения семей по числу человек в семье

Интервальный ряд распределения графически изображается в виде гистограммы. На рис.7 представлено распределение интервального ряда числа туристов в группах.

%

Рис.7 Гистограмма распределения числа туристов в группах

Накопленные частоты (частости) определяются путем последовательного прибавления к частотам (частостям) первой группы последующих групп ряда. Накопленные частоты могут быть представлены графически в виде кумуляты (рис.8 ).

%

Рис.8 Кумулята распределения туристов по численности групп

Для обеспечения сравнимости рядов распределения рассчитывают показатели плотности распределения. Абсолютная плотность распределения ( ) представляет собой величину частоты, приходящейся на единицу размера отдельной группы ряда:

.

Относительная плотность распределения ( ) – это частное от деления частости (w) отдельной группы на размер ее интервала:

.

Модуль 3. Относительные величины, вариация признаков

Блок 6. Абсолютные и относительные величины, средние величины

Абсолютные величины – это численности единиц и суммы по группам, а также по совокупности в целом, которые являются результатом сводки и группировки данных.

Абсолютные величины – именованные числа с определенной размерностью и единицей измерения.

По способу выражения размеров изучаемых явлений абсолютные величины разделяются на индивидуальные и суммарные. Индивидуальные характеризуют размеры количественных признаков у отдельных единиц совокупности, а суммарные – совокупности в целом. Для абсолютных величин важным является вопрос выбора единицы измерения. Выделяют три типа единиц измерения: натуральные, денежные и трудовые.

Натуральные величины могут быть составными. Например, работа транспорта выражается в тонно-километрах или в пассажиро-километрах, а затраты труда в человеко-часах или в человеко-днях. Применяются также условно-натуральные единицы измерения, которые получают приведением различных натуральных единиц к одной, принятой за базу для приведения к общему знаменателю. Это может быть условная банка (емкость 353,4 см³⁾ в консервной промышленности или условное топливо в топливной промышленности.

Абсолютные величины получают не всегда суммированием, они могут быть получены путем сложных расчетов. Расчетным путем могут быть получены недостающие показатели с использованием балансовых связей. Например, З_н +П = Р + З_к, З_{н =} Р + З_к – П,

где З_н и З_к – запасы на начало и конец периода, П – поступления, Р – реализация в течение периода.

Относительные величины – это производные обобщающие показатели, представленные средними и относительными статистическими величинами. Анализ предполагает сопоставление величин тех или иных показателей, в результате такого сопоставления получают качественную оценку. Относительные величины – частное от деления двух величин, где числитель – это показатель, отражающий изучаемое явление, а знаменатель – показатель, с которым производится сравнение – база сравнения. База сравнения выступает своеобразным измерителем. В зависимости от того, какое значение имеет база сравнения результат сопоставления может быть выражен в виде кратных отношений - коэффициентов, процентных отношений, промилле (расчеты на 1000), децимилле (на 10000)

Относительные величины подразделяются на следующие виды: структуры, динамики, сравнения, координации, интенсивности, выполнения планового задания, выполнения плана. Расчеты этих показателей производится путем сопоставления следующих показателей:

Относительные величины

Формула расчета

Структуры Динамики Сравнения Координации Интенсивности Планового задания Выполнения плана

Часть единиц совокупности ОВС = ------------------------------------ Общий объем совокупности Сравниваемый уровень явлений ОВД = --------------------------------------------- Уровень явления, взятый за базу сравнения Одна совокупность ОВСр=------------------------------------(одноименные) Другая совокупность Одна часть совокупности ОВК = ------------------------------------ Другая часть этой же совокупности Одна совокупность ОВИ=-------------------------------------(разноименные) Другая совокупность Плановое задание на предстоящий период ОВПЗ =-------------------------------------------------- Фактическое выполнение за базисный период Фактическое выполнение ОВВП = ------------------------------------------------- Плановое задание

Разновидностью относительных величин являются средние величины. Нахождение средних величин для совокупностей – один из наиболее распространенных способов обобщения. Бельгийский статистик А. Кетле считал выделение средних величин основным приемом статистического анализа, сами средние величины не просто мерой математического измерения, а объективной реальностью. А. Кетле выдвинул теорию «среднего человека» как некий образец, наделенный всеми качествами в среднем размере. В 19 веке эта механистическая теория была популярна и стала предметом многих научных дискуссий. Средняя величина – абстрагируется от разнообразия отдельных единиц совокупности и уходит от структуры явления. Но такое абстрагирование находится в диалектическом единстве массового и индивидуального и является необходимым приемом статистического анализа.

В статистике средние величины имеют ключевое значение, являясь сводными обобщающими показателями. Средние величины – это обобщающая или типическая характеристика исследуемого количественно варьирующего признака на определенный момент времени в расчете на единицу совокупности.

Отдельная средняя величина характеризует изучаемое явление с одной стороны, для всестороннего изучения явления требуется исследование по возможно большему числу существенных признаков. Только в этом случае можно составить объективное представление о явлении в целом и отдельных его частях.

Различные средние величины можно представить в виде формулы степенной средней:

= ,

при z= 1- средняя арифметическая;

z= 2 – средняя квадратическая;

z= 0 - средняя геометрическая;

z= -1- средняя гармоническая;

Признак, по которому определяется средняя, называется осредняемым признаком ( ͞х ), индивидуальные значения признака – варианты (х₁ , х₂ , х₃ …..х_n ), а повторяемость вариантов - частота (f).

Средняя арифметическая – наиболее часто применяемая средняя величина:

͞х = = .

Например, группа туристов из десяти человек по числу заграничных туров распределилась следующим образом: 4, 2, 5, 2, 3, 1, 3, 6, 2, 3. Среднее число туров на одного человека в группе:

͞х =

Если туристов объединить в группы по числу туров, то их среднее значение можно подсчитать как среднюю арифметическую взвешенную (табл.3):

Таблица 3

Распределение группы туристов по числу заграничных туров, в которых они побывали

Варианты числа туров xi	Число туристов fi	Общее число туров xifi
1 2 3 4 5 6	1 3 3 1 1 1	1 6 9 4 5 6
Итого:	10	31

Часто возникает необходимость вычисления средних величин для интервальных рядов. Например, необходимо рассчитать средний возраст туристов различных возрастных групп (табл. 4).

Таблица 4

Распределение групп туристов по возрасту

Группы по возрасту в годах (хi)	Число туристов (fi)	Середина интервала (x`i)	x`i fi
до 20 20 – 40 40 - 60 60 и более	2 3 4 1	10 30 50 70	20 90 200 70
Итого:	10	-	380

Средний возраст группы туристов составляет:

Средняя гармоническая – это величина обратная средней арифметической, рассчитывается из обратных значений признака:

͞x_h= (простая); ͞ x_h = (взвешенная)

применяется, когда отсутствуют частоты по исходным данным, но они входят сомножителем в один из имеющихся показателей (табл. 5).

Таблица 5

Товар, реализуемый в различных магазинах	Цена за единицу (руб.) pi	Сумма реализации (т. руб.) Qi	Объем реализации (штук) qi =
1. 2. 3. 4.	120 140 110 115	360 280 550 460	3000 2000 5000 4000
Итого:	-	1650	14000

Известны цены и общая сумма выручки за один и тот же товар в разных магазинах. Для определения физического объема реализации необходимо сумму реализации в каждом магазине разделить на цены. Среднюю цену за товар по группе магазинов можно рассчитать по средней гармонической взвешенной:

Свойства средней арифметической

Средняя арифметическая располагает рядом свойств, которые значительно упрощают расчеты на практике:

Свойство 1. Если все веса (f) увеличить или уменьшить в одинаковое число раз (а), то величина средней не изменится:

.

Свойство 2. Если каждую варианту (x) увеличить или уменьшить на одну и туже величину А, то средняя увеличится или уменьшится на ту же варианта отнять или прибавить произвольное постоянное число А, то средняя уменьшится или увеличится на то же число А:

Свойство 3. Если каждую варианту (х) увеличить или уменьшить в одно и то же число раз (i), то средняя увеличится или уменьшится в то же число раз:

Свойство 4.. Сумма отклонений отдельных вариантов от средней, взвешенных их частотами равна нулю:

Последнее свойство проверим на примере, когда турагентство организует поездки с различной дальностью:

№ тура	Дальность поездки (км.) х	Количество поездок f	xf
1 2 3 4 5	20 30 50 40 10	10 20 10 5 5	200 600 500 200 50	-11 -1 19 9 -21	-110 -20 190 45 -105
	150	50	1550	-	0

км.; .

Блок 7. Структурные средние

Структурные средние характеризуют структуру рядов распределения. К структурным средним относятся мода и медиана. Мода (Мо) – значение признака, которое наиболее часто встречается в изучаемой совокупности. В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду мода определяется по формуле:

где нижняя граница модального интервала; величина модального интервала; частоты модального, домодального и послемодального интервалов.

Модальный интервал – интервал, имеющий наибольшую частоту (частость). Например, среднедушевые доходы городского населения распределись следующим образом (табл.6).

Таблица 6

Средний душевой доход за месяц, тыс. руб.	Число жителей в % к итогу (f)	Накопленные частости (S)	Середина интервала (x)
до 5 5-10 10-15 15-20 20-25 30 и более	15 20 25 22 14 4	15 35 60 82 96 100	2,5 7,5 12,5 17,5 22,5 27,5
Итого	100	-	-

Рассчитаем модальное значение среднедушевых доходов населения города:

тыс. руб.

Наиболее частое значение среднедушевых доходов – 13125 рублей.

Медиана (Ме)- это величина, которая делит численность упорядоченного вариационного ряда на две равные части – одна часть меньше, чем средний вариант, а другая больше. Для ранжированного ряда с нечетным числом членов медианой является варианта, расположенная в центре ряда. Например, стажи работы специалистов в туристской фирме – 1,2, 2, 3, 3, 4, 5 лет – медианой является четвертая варианта – 3 года. Для ранжированного ряда с четным числом членов ряда медианой будет средняя арифметическая из двух смежных вариант, находящихся в середине ряда. Например, сотрудники туристской фирмы имеют следующие стажи работы по специальности: 2, 2, 3, 4, 4, 6 лет – медианой является значение, равное: (3+4):2=3,5 года.

Чтобы определить медиану, необходимо найти ее порядковый номер, а затем по накопленным частотам (частостям) определить величину варианта, обладающего таким номером.

Для определения медианного значения в интервальном ряду используется следующая формула:

где, нижняя граница медианного интервала; - величина медианного интервала; полусумма частот ряда; - сумма накопленных частот, предшествующих медианному интервалу; - частота медианного интервала.

Медианный интервал – интервал, в котором находится порядковый номер медианы. Для его определения подсчитывают суммы накопленных частот (частостей) до числа, превышающего половину объема совокупности.

Медианное значение среднедушевых доходов населения города составит:

тыс. руб.

Аналогичным образом могут быть рассчитаны четверти общего ряда – квартили, десятые доли – децили, сотые доли – процентили.

Блок 8. Показатели вариации

Различие индивидуальных значений признака внутри изучаемой совокупности называется вариацией признака. Колеблемость отдельных значений характеризуют показатели вариации. Различают вариацию признака случайную и систематическую. Анализ вариации позволяет оценить ее характер и определить насколько однородной является изучаемая совокупность и насколько характерной является ее средняя величина для данной совокупности.

Выделяют абсолютные и средние показатели вариации. Наиболее простой – размах вариации (R) – разность между наибольшим и наименьшим значением признака в распределении: R= .

Для получения обобщенной характеристики отклонений от средней рассчитывают среднее линейное отклонение для несгруппированных данных и для вариационного ряда показатель учитывается без знака этих отклонений.

На практике вариацию чаще оценивают с помощью показателя дисперсии в варианте без частот и

Если из дисперсии извлечь корень квадратный, то получится еще один показатель вариации – среднее квадратическое отклонение:

в варианте без частот и в варианте с частотами.

Коэффициент осцилляции характеризует относительную колеблемость крайних значений признака вокруг средней:

Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:

Наиболее распространенный показатель колеблемости, который дает обобщающую характеристику – коэффициент вариации:

Рассмотрим пример, где оценивается вариация стажа работы по специальности работников двух турфирм:

1-я 2-я

1. 4

2. 4

3. 5

4. 5

4 5

9 7

10 7

12 7

45 лет 45 лет

Проведем предварительные расчеты:

№ пп	Стаж (лет)			Стаж
1 2 3 4 5 6 7 8	1 2 3 4 4 9 10 12	-4,6 -3,6 -2,6 -1,6 -1,6 3,4 4,4 6,4	21,16 12,96 6,76 2,56 2,56 11,56 19,36 40,96	4 4 5 5 6 7 7 7	-1,6 -1,6 -0,6 -0,6 0,4 1,4 1,4 1,4	2,56 2,56 0,36 0,36 0,16 1,96 1,96 1,96
	45	-	117,88	45	-	11,88

Сопоставим показатели вариации стажа работников у двух турфирм.

1-я фирма 2-я фирма

При одинаковых средних величинах стажа работников фирм вариация признака в первой фирме в три раза выше, чем в первой.

Преобразование формулы среднего квадратического отклонения приводит ее к виду , что делает ее удобнее для практических расчетов. Этот показатель широко применяется для расчетов показателей вариации в различных отраслях знания и техники. Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты от среднего их значения.

Дисперсия альтернативного признака характеризует вариацию альтернативных признаков. Альтернативными признаками являются признаки, которыми обладают одни единицы изучаемой совокупности и не обладают другие. Например, в фирме работают мужчины и женщины, доля мужчин (р) и доля женщин (q) образуют целый коллектив сотрудников фирмы: p +q = 1. Средняя величина для альтернативных признаков равна а дисперсия . Если на фирме работает 15 мужчин и 20 женщин, то р= а , следовательно дисперсия альтернативного признака Максимальное значение дисперсии альтернативного признака равно 0,25, оно получается при р=0,5.

Правило сложения дисперсий. Если совокупность варьирующих элементов подразделить на несколько групп, то можно выделить: общую дисперсию ( ), внутригрупповую дисперсию ( ), среднюю из внутригрупповых дисперсий ( ), межгрупповую дисперсию ( ).

Общая дисперсия характеризует колеблемость признака во всей изучаемой совокупности и рассчитывается по формуле:

, где - общая средняя для всей совокупности.

Внутригрупповая дисперсия характеризует колеблемость признака внутри группы и рассчитывается по формуле:

, где - групповая средняя.

Средняя из внутригрупповых характеризует внутригрупповую колеблемость вокруг внутригрупповых средних и рассчитывается как средняя величина из внутригрупповых дисперсий:

, где - дисперсии отдельных групп, а f - численность отдельных групп.

Межгрупповая дисперсия показывает вариацию групповых средних вокруг общей средней, измеряет вариацию изучаемого признака под влиянием признака - фактора (группировочного признака) и рассчитывается по формуле:

, где и - средние и численности по отдельным группам.

Между всеми приведенными дисперсиями существует взаимосвязь, которая называется правилом сложения дисперсий – общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии:

.

Логика этого правила следующая: общая дисперсия, возникающая под влиянием всех факторов, должна быть равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии возникающей за счет фактора группировки. Зная два вида дисперсий, всегда можно определить или проверить правильность расчета третьего вида дисперсии. Например, имеются данные по среднедневной выработке сотрудников фирмы с различным стажем работы:

Группы сотрудников по стажу	Число сотрудников (f)	Средняя дневная выработка (т. руб.)	Дисперсия выработки
До 5 лет	40	120	450
Более 5 лет	60	160	500

т. рублей

, следовательно: .

В статистике применяется показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии, который показывает, какая часть общей вариации изучаемого признака обусловлена вариацией группировочного признака. Это коэффициент детерминации, рассчитываемый по формуле: .

Если извлечь корень квадратный из коэффициента детерминации, получаем новый показатель, который носит название корреляционное отношение:

.

Блок 9. Изучение формы распределения

В вариационных рядах существуют определенные зависимости между частотами и значениями варьирующего признака. Как правило, с увеличением варьирующего признака величина частот сначала увеличивается до определенной величины, а затем уменьшается.

Рассеивание кривой распределения по оси абсцисс является показателем колеблемости признака; чем больше рассеивание, тем больше колеблемость признака. Положение кривой распределения на оси абсцисс и ее рассеивание являются двумя наиболее существенными свойствами кривых распределений. Определение формы кривой является важнейшей задачей изучения распределений. В практике исследований встречаются всевозможные распределения. Подавляющая часть распределений подчиняется закону нормального распределения. Кривая отображающая это распределение имеет на плоскости вид колокола и она симметрична. В идеальном случае нормального распределения значения средней арифметической, моды и медианы совпадают.

Определение общего характера распределения предполагает оценку его однородности, а также вычисление асимметрии и эксцесса. Симметричным является распределение, где частоты равноотстоящие в обе стороны от центра распределения, равны между собой. Как правило, абсолютная симметрия в природе не встречается. Но с увеличением числа наблюдений кривые сглаживаются и приходят к кривой распределения, которая все более приближается к нормальному распределению.

Показатель асимметрии основан на сопоставлении с центром распределения: чем меньше разница между или , тем меньше асимметрия ряда и наоборот.

Для сравнительного анализа асимметрии определяют относительный показатель асимметрии:

или

Величина показателя может быть положительной и отрицательной. Положительный показатель свидетельствует о наличии правосторонней асимметрии и при этом имеется следующее соотношение между показателями: .

Отрицательный знак показателя асимметрии указывает на наличие левосторонней асимметрии и здесь имеется следующее соотношение между показателями:

Линдберг предложил другой показатель асимметрии: , где n –процент тех значений признака, которые превосходят по величине среднюю арифметическую.

Наиболее точный показатель асимметрии опирается на определение центрального момента третьего порядка:

, где - центральный момент третьего порядка определяется как: .

При анализе вариационных рядов предполагается также определение эксцесса распределения. Эксцесс – это оценка на островершинность и плосковершинность распределения по отношению к нормальному распределению. Эксцесс определяется только для симметричных и умеренно асимметричных распределений. Наиболее часто используется следующий показатель:

, где - центральный момент четвертого порядка:

Распределения более островершинные, чем нормальные обладают положительным эксцессом ( ) и отрицательным эксцессом, если распределение более плосковершинное, чем нормальное распределение ( ).

Модуль 4 . Выборочное наблюдение

Блок 10. Содержание выборочного наблюдения, ошибки выборочного наблюдения

Мы уже знаем, что если возникает необходимость проведения наблюдения, то оно может проводиться как сплошное наблюдение, когда обследуются все без исключения единицы наблюдения и как несплошное наблюдение, когда обследуется только определенная часть общей совокупности.

Выборочное наблюдение – основной вид из ряда способов несплошного наблюдения. Выборочным называется наблюдение заранее определенного числа единиц совокупности, отобранных в особом порядке. Выборочный метод исследования предполагает получение обобщающих показателей изучаемой совокупности по обследованной ее части. При этом подлежащая исследованию совокупность называется генеральной совокупностью, а отобранная из генеральной совокупности ее часть называется выборочной совокупностью.

Выборочный метод позволяет при минимальной численности обследуемых единиц получить объективные характеристики всей изучаемой совокупности. Это особенно актуально в современных условиях, когда сплошные наблюдения дороги и не всегда эффективны. Теория и опыт показали, что при правильной организации выборочного наблюдения можно получить достоверные данные о изучаемой совокупности. Эти данные (абсолютные и относительные) достаточно точно воспроизводят – репрезентируют всю совокупность. Выборочные наблюдения практикуются во всех видах социальной и экономической деятельности.

Для более глубокого изучения выборочного метода введем некоторые условные обозначения:

N – объем генеральной совокупности – число входящих в нее единиц;

n - объем выборочной совокупности – число единиц, попавших в выборку;

генеральная средняя – среднее значение изучаемого признака в генеральной совокупности;

выборочная средняя – среднее значение изучаемого признака в выборочной совокупности;

р - генеральная доля – доля единиц, обладающих данным признаком в генеральной совокупности;

w - выборочная доля – доля единиц, обладающих данным признаком в выборочной совокупности; где m- число единиц, обладающих изучаемым признаком, n – объем выборочной совокупности;

генеральная дисперсия - дисперсия изучаемого признака в генеральной совокупности;

выборочная дисперсия – дисперсия изучаемого признака в выборочной совокупности;

среднее квадратическое отклонение изучаемого признака в генеральной совокупности;

среднее квадратическое отклонение изучаемого признака в выборочной совокупности.

Ошибки выборочного наблюдения

При любом наблюдении (сплошном и несплошном) возникают ошибки при регистрации единиц наблюдения. Такие ошибки называются ошибками регистрации. Они могут быть случайными и систематическими, это связано в значительной степени с субъективным фактором, который всегда присутствует при организации и проведении наблюдения.

При проведении выборочных наблюдений, помимо ошибок регистрации, возникают случайные ошибки репрезентативности (представительности), которые возникают в связи с тем, что отобранная для наблюдения часть общей совокупности имеет отличную от генеральной n

Научным обоснованием случайных ошибок выборки являются теория вероятностей и ее предельные теоремы. Используются теоремы русских математиков П.Л. Чебышева и А.М. Ляпунова. В соответствии с этими теоремами, с увеличением численности выборки размеры случайных ошибок сокращаются, что при достаточно большом объеме выборки случайная ошибка будет сколь угодно мала и что характеристики выборочного наблюдения будут надлежащим образом представлять генеральную совокупность.

Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются средней ошибкой выборки . Под средней ошибкой выборки понимают расхождение между средними выборочной и генеральной совокупности ( , которое не превышает . В математической статистике доказано, что значение средней ошибки выборки определяются по формуле:

где дисперсия изучаемого признака х в выборочной совокупности, а n – численность выборочной совокупности.

Соответственно для расчета средней ошибки доли изучаемого признака используется формула:

где pq – где дисперсия доли изучаемого признака, а n – численность выборочной совокупности. Следовательно, для уменьшения средней ошибки выборки в 3 раза необходимо увеличить объем выборки в 9 раз.

Рассмотрим условный пример. Генеральная совокупность – число сделок N =1000

Доходность сделок (тыс. руб.) Число сделок

12.  200

14 500

15 300

Всего: 1000

Средня доходность:

тыс. руб.

Дисперсия:

Доля сделок с доходностью 14 и более тыс. рублей р= или 80%

Предположим, что случайным образом отобрана информация о 200 сделках и получены данные о средних и относительных показателях:

Доходность сделок (тыс. руб.) Число сделок

12. 34

14 100

15 66

Всего: 200

Средняя доходность тыс. руб.

Дисперсия

Доля сделок с доходностью 14 и более тыс. рублей w= или 83%.

Сведем полученные показатели в таблицу:

Показатели Генеральная совокупность Выборочная совокупность Средняя доходность Дисперсия доходности Доля сделок с доходностью более14 тыс. рублей 13,90 1,09 0,80 13,99 1,01 0,83

Теперь можно определить среднюю ошибку выборки:

Для средней доходности ;

Для доли 14 и более т. руб. .

Предельная ошибка выборки

Средняя ошибка выборки используется для определения возможных отклонений показателей выборочной совокупности от соответствующих показателей генеральной совокупности.

С определенной вероятностью можно утверждать, что эти отклонения не превысят заданной величины - предельная ошибка выборки, Этот показатель определяется по формуле: где t – коэффициент, зависящий от вероятности, с которой можно гарантировать определенные размеры предельной ошибки; этот коэффициент называется коэффициентом доверия. Этот коэффициент определяется по таблице значений интегральной функции Лапласа при заданной доверительной вероятности. Ниже приведены наиболее часто употребляемые уровни вероятности и соответствующие значения t.

	0,683	0,950	0,954	0,990	0,997
t	1,00	1,96	2,00	2,58	3,00

С увеличением t величина вероятности быстро приближается к единице. Увеличивая численность выборки n , можно отклонение выборочной средней от генеральной ( ) довести до сколь угодно малых размеров.

Основные виды выборки

Индивидуальный отбор единиц наблюдения должен производиться из генеральной совокупности таким образом, чтобы обеспечить всем единицам одинаковую возможность попасть в выборку. Если это условие соблюдается, то это собственно случайная выборка.

Если совокупность разбивается на однородные группы единиц, из которых производится индивидуальный отбор, то это типичная или районированная выборка.

Если вместо индивидуального отбора выбираются серии единиц и в них производится сплошное наблюдение, то это

Отбор единиц наблюдения из общей совокупности может производиться повторно и бесповторно. Повторный отбор предполагает, что каждая единица наблюдения может принять участие в отборе несколько раз, т.е. каждый раз при отборе единица возвращается в общую совокупность. При бесповторном отборе выбранная единица не участвует в дальнейшем отборе.

При расчете ошибок возникает существенное затруднение – величины и р по генеральной совокупности как правило неизвестны. Эти величины заменяют выборочными величинами - и . В таблице приведены формулы расчета предельных ошибок выборки.

Способы отбора	При определении средней	При определении доли
Повторный Бесповторный

По данным вышеприведенного примера рассчитаем предельную ошибку выборки c вероятностью 0,954 при бесповторном отборе:

N=1000, n=200, .

1. для средней т. руб.

2. для доли или

С вероятностью 0,954 можно утверждать, что разность между выборочной средней и генеральной средней не превышает по абсолютным размерам - 0,13 тыс. рублей, а между частостью и долей - 0,0475. Доверительный интервал, в котором может находиться средняя и доля:

, или

.

Для нашего примера доверительный интервал:

13,99-0,13 или может находиться в диапазоне от 13,83 до 14,12.

0,83-0,0475 или р может находиться в диапазоне от 0,7825 до 0,8775.

На практике часто ставится задача определения объема выборочной совокупности при заранее заданной предельной ошибке выборки. В этом случае используются формулы, выведенные из формул ошибок выборки:

Способы отбора	При определении средней	При определении доли
Повторный Бесповторный

При определении n точные данные о генеральной дисперсии, как правило, не известны, поэтому используют данные прежних обследований и их дисперсий. При полном отсутствии данных вариации альтернативного признака вместо pq подставляют максимальное значение дисперсии – 0,25.

По данным вышеприведенного примера рассчитаем объем необходимой выборки. Необходимо определить, какое количество сделок нужно отобрать для выборочного наблюдения, чтобы ошибка выборки с вероятностью 0,954 не превышала 0,1 тыс. рублей для средней и 3% для доли при бесповторном отборе. Для решения этой задачи имеем следующие условия:

N=1000;

Для определения средней доходности сделок:

=

= .

При заданных условиях для определения средней величины доходности сделок необходимо отобрать информацию о не менее 304 сделках, а для определения доли сделок с доходностью 14 и более тыс. рублей необходимо отобрать информацию о не менее 416 сделках.

Блок 11. Малая выборка

Малая выборка – это несплошное статистическое наблюдение, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Обычно объем малой выборки не превышает 30 единиц, а минимальный объем может доходить до 4-5 единиц. В отдельных случаях к малой может быть отнесена выборка до 45 единиц. Малая выборка широко применяется в экономических исследованиях и при организации контроля качества товаров и услуг.

Средняя ошибка малой выборки определяется по формуле:

где - дисперсия малой выборки, она рассчитывается по формуле

= , где n-1- число степеней свободы.

Предельная ошибка малой выборки рассчитывается по формуле:

Коэффициент доверия t зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n . Для отдельных значений t и n доверительная вероятность малой выборки определяется по специальным таблицам Стьюдента, где даны распределения стандартизированных отклонений:

.

Для проведения малой выборки в качестве доверительной вероятности принимается 0,95 и 0,99. Для определения предельной ошибки малой выборки используют распределения Стьюдента и определяют коэффициент доверия t:

n	S(t)
	0,95	0,99
4 5 6 7 8 9 10 15 20	3,183 2,777 2,571 2,447 2,364 2,307 2,263 2,119 2,078	5,841 4,604 4,032 3,707 3,500 3,356 3,250 2,921 2,832

Пример. При анализе прибыли по сделкам, совершенным фирмой в течение года, была сделана выборка и установлена по ним прибыльность в %: 4,5; 5,0; 4,2; 3,5; 6,0; 5,2; 4,5; 5,2; 4,3; 6,6.

Нужно по данным выборочного наблюдения установить с вероятностью 0,95 предел, в котором находится средняя прибыльность сделок, по результатам работы фирмы за год.

Средняя прибыльность сделок по данным малой выборки:

Определяем дисперсию малой выборки; для этого произведем предварительные расчеты:

Прибыльность сделок		(
4,5 5,0 4,2 3,5 6,0 5,2 4,5 5,2 4,3 6,6	-0,4 0,1 -0,7 -1,4 1,1 0,3 -0,4 0,3 -0,6 1,7	0,16 0,01 0,49 1,96 1,21 0,09 0,16 0,09 0,36 2,89
49,0	-	7,42

= =

Определяем среднюю ошибку малой выборки:

Находим предельную ошибку малой выборки. Для этого по распределению Стьюдента при заданной вероятности находим значение коэффициента доверия t= 2,263

2,263

Следовательно, с вероятностью 0,95 можно утверждать, что средняя годовая прибыльность сделок фирмы находится в пределах:

т.е. от 4,9-0,66=4,24% до 4,9+0,66=5,56%.

Модуль 5. Статистические методы прогнозирования процессов в туризме

Блок 12. Ряды динамики. Исследование основных тенденций развития явлений в туризме

Все социально-экономические явления развиваются во времени. Динамизм явлений является результатом взаимодействия многих причин и факторов. Изучение динамики развития явлений преследует цель – выявление и измерение тенденций и закономерностей их развития. Для того, чтобы можно было проанализировать явления в развитии, необходимо построить ряды динамики.

Рядами динамики называются статистические данные, отображающие развитие явления во времени. Ряды динамики имеют два основных элемента:

1. уровни, характеризующие величину признака;

2. периоды, к которым относятся уровни.

Ряды динамики могут быть: моментными, когда состояние явления фиксируется на какой-то момент и интервальными, когда явление отражается за отдельные периоды времени.

С помощью рядов динамики осуществляется изучение закономерностей развития социально-экономических явлений по следующим направлениям: 1) характеристика уровней развития явлений во времени; 2) измерение динамики развития явлений с помощью системы статистических показателей; 3) выявление и количественная оценка основных тенденций развития явлений (тренда); 4) изучение периодических колебаний в развитии явлений; 5) экстраполяция и прогнозирование развития явлений.

Основным условием правильного построения ряда динамики является сопоставимость его элементов. Ряды динамики формируются в результате сводки и обработки материалов периодических наблюдений. Повторяющиеся во времени значения отдельных показателей систематизируются в хронологической последовательности. При этом ряды динамики охватывают отдельные периоды времени, когда изучаемые явления могут находиться в различных условиях, которые могут привести к несопоставимости отчетных данных с данными других периодов. В этих случаях необходимо приведение всех составляющих элементов к сопоставимому виду. Для этого проводится анализ причин, приведших к несопоставимости полученной информации и применяется соответствующая обработка, позволяющая привести показатели к сопоставимому виду.

Причины несопоставимости показателей в рядах динамики могут быть различными. Это может быть разновеликость показателей времени, неоднородность состава изучаемых совокупностей во времени, изменение методики первичного учета и сводки исходной информации, различия применяемых единиц измерения, ценовые изменения и т.д.

Данные могут быть несопоставимыми по кругу охватываемых объектов. Например, в городе сначала было 14 гостиниц, затем в строй действующих в 2002 г. было введено еще две. Изучение динамики валовой продукции (услуг) гостиниц во времени стали несопоставимыми. Привести к сопоставимости динамического ряда можно следующим образом:

Показатели	2000 г.	2001 г.	2002 г.	2003 г.	2004 г.	2005 г.
Валовая продукция 14-и гостиниц (млн. руб.)	34	39	43
Валовая продукция 16-и гостиниц (млн. руб.)			48	52	55	61
В %% к уровню 2002 г.	79,0	90,0	100,0	108,3	114,5	127,0

Для того, чтобы динамический ряд сделать сопоставимым 2002 г., когда были введены в стой действующих еще две гостиницы, был принят за 100%.

Уровни динамического ряда могут быть рассчитаны различными способами. Например, часть показателей зафиксированы на определенную дату, а другая часть рассчитана как среднегодовая численность. В этом случае необходимо провести перерасчет данных и привести к их к одному показателю.

Характеристики динамики

Для количественной оценки динамики развития явлений используются статистические показатели динамики: абсолютные приросты, темпы роста и прироста, которые дают характеристику направления и размер изменений явления во времени. Рассмотрим условный пример с потоками туристов в регион в течение ряда лет:

Год	2000	2001	2002	2003	2004	2005
Количество туристов, млн. чел.	1,155	1,170	1,201	1,280	1,320	1,410

Средний уровень динамики для интервальных рядов представим как где n – число уровней. млн. человек.

Для моментных рядов фиксируется состояние явления на определенный момент, это могут быть данные на начало или конец какого-либо периода (например, по состоянию на 1 января текущего года). Средний уровень здесь определяется как средняя арифметическая из двух этих показателей. Например, численность работников турфирмы на 1 января.

Годы	2003	2004	2005	2006	2007
Человек	60	72	84	90	102

60 человек на 1 января 2003 г. – это одновременно численность работников фирмы на 31 декабря 2002 г. Поэтому средняя численность работников:

за 2003 г. чел. за 2004 г. =78 чел.

за 2005г. чел. за 2006 г. чел.

Средняя численность за период составила чел.

Средний уровень моментного ряда рассчитывается также по средней хронологической:

Например, имеются данные о числе гостей в отеле по состоянию на начало квартала в течение 2005 года.

Кварталы	01.01	01.04	01.07	01.10	01.01.06
Число гостей	85	92	120	87	83

Средняя численность гостей в течение года:

чел.

В динамических рядах определяют вариацию динамики по формулам:

и

С помощью простейших показателей определим направление и размер изменений уровней во времени по данным потоков туристов в регионе в течение ряда лет:

Год	2000	2001	2002	2003	2004	2005
Количество туристов, млн. чел. у	1,155	1,170	1,201	1,280	1,320	1,410
Ежегодный абсолютный прирост	-	0,015	0,031	0,079	0,040	0,090
Темп роста к предыдущему году	-	1,013	1,026	1,066	1,031	1,068
Темп роста в %	-	101,3	102,6	106,6	103,1	106,8
Темп прироста к предыдущему году	-	1,3	2,6	6,6	3,1	6,8
Темп роста к 2000 г. (%)	100,0	101,3	103,9	110,8	114,3	122,1
Темп прироста к 2000 году	-	1,3	3,9	10,8	14,3	22,1

Исследование тенденций развития явлений

Изменение уровней рядов динамики связано с влиянием на изучаемое явление множества факторов, которые различны по силе воздействия, направлению и времени их действия. Постоянно действующие факторы оказывают на явление определяющее воздействие и формируют в рядах динамики основное направление развитие – тренд. Воздействие других факторов, как правило, периодическое и вызывает колебания уровней рядов динамики. Определенное воздействие на динамику развития явления могут оказывать отдельные случайные (спорадические) факторы.

Воздействие постоянных, периодических и разовых причин на уровни динамики развития явления вызывает необходимость изучения этих факторов для определения тренда, периодических колебаний и случайных отклонений.

Простейший способ обработки динамического ряда с целью выявления тенденции его развития заключается в укрупнении интервалов времени. Предположим, имеются данные о количестве гостей в отеле по месяцам в течение года:

Месяц	Количество гостей	Месяц	Количество гостей
Январь Февраль Март Апрель Май Июнь	102 108 103 106 104 112	Июль Август Сентябрь Октябрь Ноябрь Декабрь	120 120 115 109 105 108

Укрупним интервалы до трех месяцев, рассчитаем общее количество гостей и среднемесячное их количество по кварталам:

Квартал	Количество гостей	Среднемесячное количество гостей по кварталам
I II III IY	313 322 355 322	104 107 118 107

Укрупнив интервалы, устранили случайные колебания и проявили основную тенденцию сезонных колебаний в потоке гостей в течение года.

Сглаживание способом скользящей средней. Суть этого способа заключается в замене фактических уровней рядом подвижных (скользящих) средних, которые рассчитываются для последовательно подвижных интервалов и относятся к середине каждого из них. Сглаживание этим способом можно производить по любому числу членов ряда. Если осуществляется сглаживание ряда динамики с интервалом из 5 членов, то в этом случае необходимо последовательно суммировать по 5 членов и результаты делить на 5. Например, поток туристов в страну в течение 10 лет составил:

Годы	Поток туристов млн. человек	Скользящая сумма из 5 членов	Скользящая средняя
1 2 3 4 5 6 7 8 9 10	4,3 4,6 4,3 4,5 4,3 5,2 5,3 5,7 6,0 6,0	- - 22,0 22,9 23,6 25,0 26,5 28,0 - -	- - 4,40 4,58 4,72 5,00 5,30 5,64 - -

Недостатком сглаживания ряда способом скользящей средней является то, что сглаженный ряд укорачивается по сравнению с фактическим на члена с одного и другого конца (n- число членов, из которых рассчитываются скользящие средние). В нашем случае это по с каждой стороны.

Выравнивание по аналитическим формулам. Этот способ обработки динамических рядов является более совершенным по сравнению с вышеприведенными способами. Способ предполагает подбор наиболее подходящей функции, для отражения тенденции развития изучаемого явления. Задача выравнивания здесь сводится к определению вида функции, отысканию ее параметров по эмпирическим данным и расчету теоретических уровней по найденной формуле.

К наиболее простым формулам, отражающим тенденции развития относятся:

1) прямая вида , где -теоретический уровень, t – время, a и b – параметры прямой.

2) парабола второго порядка

3) показательная функция

4) гипербола .

Выравнивание по прямой. Как правило, используется в тех случаях, когда абсолютные приросты относительно постоянны, т.е. когда уровни изменяются приблизительно в рамках арифметической прогрессии.

Параметры a и b искомой прямой находятся решением системы нормальных уравнений:

,

где y- уровни эмпирического ряда,n –количество уровней ряда, t- время

Эту систему можно упростить, если отсчет моментов времени ведется от середины ряда. При нечетном числе уровней ряда средняя точка принимается за 0, тогда предшествующие периоды обозначаются: -1,-2,-3 и т.д., а последующие за средним: +1,+2,+3 и т.д. В сумме t должно сводиться к 0.

При четном числе уровней ряда два серединных момента времени принимаются за -1 и +1 и все остальные соответственно обозначаются через два интервала:-5, -3, -1, +1, +3, +5, В этом случае и система уравнений принимает вид:

b , тогда , .

Рассмотрим условный пример с потоками туристов в регион в течение 5 лет:

Годы	Поток туристов, тыс. чел. (y)	Условное обозначение времени (t)	t2	yt
2000 2001 2002 2003 2004	110 115 120 125 131	-2 -1 0 +1 2	4 1 0 1 4	-220 -115 0 125 262	109,8 115,0 120,2 125,4 130,6
n=5				52	601

Определяем параметры: , b=

Тогда уравнение теоретической прямой будет иметь вид: . Подставляя последовательно значения t=-2, -1, 0, 1, 2 находим выравненные уровни динамического ряда.

Выравнивание по параболе 2-го порядка. Выравнивание по параболе 2-го порядка сводится к нахождению параметров a,b,c из системы нормальных уравнений:

.

При система уравнений имеет вид:

.

Произведем выравнивание динамического ряда объема услуг фирмы за 6 лет параболой 2-го порядка:

Годы	Объем услуг, млн. руб. (у)	t	t2	t4	ty	t2 y	уt= 53,73+6,22t+0,28t2
2000 2001 2002 2003 2004 2005	29,9 37,3 47,2 60,9 75,2 91,5	-5 -3 -1 1 3 5	25 9 1 1 9 25	625 81 1 1 81 625	-149,5 -111,9 -47,2 60,9 225,6 457,5	747,5 335,7 47,2 60,9 676,8 2287,5	29,6 37,6 47,8 60,2 74,9 91,9
Итого n=6	342,0	0	70	1414	435,4	4155,6	342,0

Полученные суммы по столбцам подставим в систему уравнений:

6 а₀ + 70 а₂ = 342

70 а₁ = 435,4

70 а₀ +1414 а₂ = 4155,6

Решив уравнение, находим: а₀ = 53,73; а₁ = 6,22; а₂ = 0,28.

Отсюда искомое уравнение параболы 2-го порядка у_t= 53,73+6,22t+0,28t² . На основе этого уравнения рассчитаем выравненные уровни, подставив соответствующие значения t и занесем их в последнюю графу таблицы.

Выравнивание по показательной функции. В основном производится, когда динамический ряд отражает развитие процесса в геометрической прогрессии. Уравнение показательной функции . Логарифм показательной функции представляет собой уравнение прямой Заменив уровни ряда их логарифмами, параметры a и b можно определить через их логарифмы. Система уравнений подобна системе уравнений при выравнивании по прямой.

Е сли , то система сводится к следующему виду:

Отсюда и .

Произведем выравнивание динамического ряда продаж турфирмой туристских путевок в течение 7 лет:

Годы	Количество проданных путевок, тыс. шт.(у)	lg y	Условное обозначение времени t	t2	t lgy	lg yt	Выравненные уровни yt
2000 2001 2002 2003 2004 2005 2006	108 111 115 118 121 124 128	2,0334 2,0453 2,0607 2,0719 2,0828 2,0934 2,1072	-3 -2 -1 0 1 2 3	9 4 1 0 1 4 9	-6,1002 -4,0906 -2,0607 0 2,0828 4,1868 6,3216	2,0344 2,0465 2,0586 2,0707 2,0828 2,0949 2,1070	108,2 111,3 114,5 117,7 121.0 124,5 127,9
n=7	825	14,4947	0	28	0,3397	14,4949	825,1

lg a=

lg b= ,

следовательно, или .

Подставляем в формулу значения t , найдем логарифмы , а затем по таблицам - .

Для 2000 г. lgy=2,0707+0,0121(-3)=2,0344 или .

Выравненные уровни близки к эмпирическим уровням, значит показательная функция подходит для отражения тренда.

Блок 13. Прогнозирование на основе изучения тренда

Построение прогнозов, чаще всего сводится к экстраполяции тенденции. Под экстраполяцией понимается распространение выявленных в ходе анализа рядов динамики закономерностей развития изучаемого явления на будущее. Основой прогнозирования является предположение о том, что закономерность, действующая внутри исследуемого ряда динамики, сохранится и в дальнейшем.

Важное значение при экстраполировании тренда имеет продолжительность базового ряда динамики и срока прогноза. Базовый ряд динамики при прогнозировании социально-экономических явлений целесообразно выбирать таким образом, чтобы он представлял определенный этап в развитии изучаемого явления. Сроки прогнозирования l зависят от поставленных задач исследования. При этом необходимо учитывать тот факт, что чем короче сроки прогноза, тем надежнее результаты экстраполяции.

При экстраполяции уровней развития изучаемого явления на основе ряда динамики с относительно постоянными абсолютными приростами используется формула:

, где - экстраполируемый уровень, конечный уровень базисного ряда динамики, l- срок прогноза.

При прогнозировании тренда изучаемого явления на основе аналитического выравнивания для экстраполяции тренда применяется модель, которая наиболее адекватно отражает тенденцию развития явления. Рассмотрим экстраполяцию тренда динамики продаж туристских путевок на 2008 г. трендовая модель - . Для прогнозирования уровня продаж на 2008 г. в модель подставим t=4, тогда 131,5 тыс. штук путевок.

На практике результат экстраполяции прогнозируемых уровней оценивается интервальными оценками. Для определения границ интервалов используется формула:

, где - коэффициент доверия по распределению Стьюдента, - остаточное среднее квадратическое отклонение тренда, скорректированное по числу степеней свободы (n-m); n- число уровней базисного ряда динамики, m- число параметров условного времени для модели тренда.

Для нашего примера число степеней свободы при n=7 и m=4 составит 3. При уровне значимости , коэффициент доверия по таблице Стьюдента равен 3,18. Для расчета среднего квадратического отклонения необходимо произвести предварительные расчеты:

Годы	Эмпирические уровни	Теоретические уровни	yi -
2000 2001 2002 2003 2004 2005 2006	108 111 115 118 121 124 128	108,2 111,3 114,5 117,7 121,0 124,5 127,9	-0,2 -0,3 0,5 0,3 0 -0,5 0,1	0,04 0,09 0,25 0,09 0 0,25 0,01
	825	825,1		0,69

При 0,69 значение остаточного среднего квадратического отклонения = Значение вероятностных границ интервала составит: 131,5 Следовательно, с вероятностью 0,95 верхняя граница объема проданных туристских путевок в 2007 г. составит 131,5+0,48=131.98 тыс. путевок, а нижняя граница – 131,5-0,48=131,02 тыс. путевок.

Блок 14. Изучение сезонных колебаний в туризме

Сезонность – важнейший фактор, определяющий интенсивность потоков туристов и связанные с этим колебания спроса на услуги туризма. Сезонные колебания определяют потоки туристов, цены на турпродукты и множество сопутствующих факторов.

Различают четыре сезона туристской деятельности:

Сезон пик - наиболее благоприятный период для организации рекреационной деятельности, когда наблюдается максимальный поток туристов;

Сезон высокий - период, когда наблюдается высокая деловая активность в туристском бизнесе. Это время, когда наиболее высокие цены на услуги индустрии туризма;

Сезон низкий – период спада деловой активности на рынке туристских услуг. Для этого периода характерны низкие цены на туристский продукт и услуги;

«Мертвый» сезон – неблагоприятный период для рекреационной деятельности и максимального спада туристских потоков.

Сезонный фактор в туризме определяет спрос на туристские услуги, оказывает влияние на рентабельность деятельности предприятий сферы туризма и занятость работников индустрии туризма.

С точки зрения статистики сезонность – это устойчивые внутригодовые колебания уровней развития явлений. Практическое значение в изучении сезонных колебаний состоит в том, что получаемые в ходе анализа количественные характеристики отражают специфику развития явления во внутригодовой динамике, что позволяет установить закономерности развития, прогнозировать развитие явления и принимать квалифицированные управленческие решения.

Сезонность услуг туризма обусловлена многими факторами, это не только время года; важное значение здесь имеют периоды отпусков, каникул, праздников и ряд других факторов.

Сезонные колебания измеряются с помощью индексов сезонности, которые определяются как процентное отношение исходных (эмпирических) уровней ряда динамики к теоретическим (расчетным) уровням, выступающим в качестве базы сравнения:

, где эмпирический уровень ряда, - теоретический уровень ряда. Для каждого периода годового цикла определяются средние индексы:

Применение формул для изучения сезонных колебаний проиллюстрируем на примере квартальных потоков гостей в отеле в течение трех лет. Для получения теоретического уровня тренда используем прямолинейную функцию

Годы	Кварталы	Условное обозначение времени (ti )		Количество гостей yi	ti yi	Теоретические уровни	Индекс сезонности
2005	I II III IY	-11 -9 -7 -5	121 81 49 25	410 505 606 380	-4510 -4545 -4242 -1900	467,9 471,6 475,3 479,0	87,6 107,1 127,5 79,3
2006	I II III IY	-3 -1 1 3	9 1 1 9	415 508 640 370	-1245 -508 640 1110	482,7 486,4 490,0 493,7	86,0 105,2 130,6 74,9
2007	I II III IY	5 7 9 11	25 49 81 121	420 550 650 405	2100 3850 5850 4455	497,4 501,1 504,8 508,4	84,4 109,8 128,8 79,7
	12	0	572	5859	1055	5858,3	-

a_{0= , ,}

.

Для первого квартала 2005 г. и т.д.

Индекс сезонности для первого квартала 2005г. рассчитывается по формуле: и т. д.

Для устранения действия факторов случайного характера производится усреднение индивидуальных индексов сезонности. Для этого производится расчет средних индексов сезонности по одноименным кварталам:

I квартал ;

II квартал

III квартал ;

IYквартал .

Вычисление средних индексов сезонности представляет собой модель сезонной волны потока гостей отеля в течение года, когда пик сезонности приходится на III квартал, а «мертвый» сезон - на IY квартал.

Модуль 6. Индексный метод

Блок 15. Понятие индекса, виды индексов

Статистический индекс – это относительная величина изменения значений одного признака взятого и рассматриваемого не изолированно, а в системе показателей. В статистике индексы – это относительные величины, характеризующие состояние явления во времени, в пространстве или в соотношении фактических данных с запланированными.

Индексы могут оценивать изменение явлений практически во всех сферах деятельности. Они подразделяются на количественные, которые характеризуют объемы в абсолютных величинах (объемы производства, реализации, перевозок, численности работников, туристов и т.д.) и на качественные, которые обычно выражаются в средних величинах (цены, заработная плата, себестоимость, производительность труда и т.д.).

Также индексы подразделяются на индивидуальные и общие. Индивидуальные индексы характеризуют изменения отдельных единиц совокупности; общие индексы выражают сводные результаты совместного изменения всех единиц совокупности.

Особенностью индексов является то, что они обладают синтетическими и аналитическими свойствами. Синтетические свойства состоят в том, что этот метод позволяет соединять в целое разнородные единицы совокупности, а аналитические свойства состоят в том, что с помощью индексного метода можно определять влияние отдельных факторов на изменение изучаемого показателя.

Для определения индекса производится сопоставление как минимум двух величин, при этом сравниваемая величина (числитель) принимаемая за текущий период, а величина с которой производится сравнение (знаменатель) – это базисный период. Основным элементом индексного отношения является индексируемая величина – это значение признака совокупности, изменение которой является объектом изучения. Например, индекс цен на туристические услуги за ряд лет. Индивидуальные индексы принято обозначать i , а общие индексы I. Применяются условные обозначения индексируемых величин: q – объемные показатели, р- цена, с- себестоимость, w- производительность труда и т.д.

Индивидуальные индексы физического объема определяются по формуле: где q₁- физический объем изучаемого явления в отчетный период, q₀ – физический объем того же явления в базисный период. Индивидуальный индекс цен: и т. д.

Агрегатные индексы

Основной формой общих индексов являются агрегатные индексы. Их происхождение связано с латинским словом «aggrega», которое означает «присоединяю». В индексной системе сопоставимость разнородных единиц достигается введением специальных сомножителей, которые называются соизмерителями. В качестве соизмерителей выступают такие показатели как цены, объемы, себестоимость и т.д. Например, в течение текущего месяца реализовано путевок (q=20) по средней цене за путевку (р=15 000 рублей), тогда общий объем реализации путевок составит рублей. В прошлом месяце было реализовано путевок (q₀=15) по средней цене (р₀=14500 рублей), тогда общий объем реализации в базисном периоде будет рублей, а общий индекс товарооборота составит: или 137,9%, что означает увеличение объема реализации путевок на 37,9% в отчетном месяце по сравнению с базисным.

Индексы количественных показателей. Типичным индексом количественных показателей является индекс физического объема. Если имеется несоизмеримая в единицах измерения продукция (услуги) предприятия, то в качестве соизмерителя берется цена за единицу продукции (услуги). Общий индекс получают сопоставлением итогов деятельности предприятия в отчетном периоде с базисным:

чтобы отразить влияние изменения объемных показателей (q) на общее изменение стоимости продукции в отчетном периоде по сравнению с базисным периодом, используют агрегатный индекс физического объема (I_q), где в качестве соизмерителя выступает цена за единицу продукции (услуги) (р):

, здесь индексируемой величиной выступает q. Посмотрим, как это выглядит на примере. Допустим, турфирма предлагает три вида продукции по разным ценам в отчетном и базисных периодах.

Турпродукты	q0 количество в базисном периоде	p0 цена за единицу в базисном периоде (тыс. руб.)	q1 количество в отчетном периоде	p1 цена за единицу в отчетном периоде (тыс. руб.)	q0p0 Оборот в базисном периоде	q1p0 Оборот в отчетном периоде по базисным ценам
А Б В	50 20 60	15 10 5	60 30 70	13 9 4,5	750 200 300	900 300 350
Итого:	-	-	-	-	1250	1550

или 124%. Это означает, что общий оборот турпрoдукции в отчетном периоде увеличился на 24%, а в денежном выражении на 1550-1250= 300 тыс. рублей.

Индексы качественных показателей. Рассчитываются на единицу продукции. К индексам качественных показателей относятся индексы цен, себестоимости, производительности труда и т. д. Для определения индивидуальных индексов цен применяется формула . Основной формой общих индексов являются агрегатные индексы. При определении общего индекса цен в качестве соизмерителя, как правило, выступают количественные показатели объема производства или реализации товаров (услуг) в текущем периоде - q₁. Агрегатная формула такого общего индекса имеет вид:

Расчет агрегатного индекса цен был предложен немецким экономистом Г. Пааше, поэтому его называют индексом Пааше. Рассчитаем индекс цен для нашего примера с турпродуктами.

Турпродукты	q0 количество в базисном периоде	p0 цена за единицу в базисном периоде (тыс. руб.)	q1 количество в отчетном периоде	p1 цена за единицу в отчетном периоде (тыс. руб.)	р1q1 Оборот в отчетном периоде	p0q0 Оборот в базисном периоде	p0q1 Оборот в отчетном периоде по базисным ценам
А Б В	50 20 60	15 10 5	60 30 70	13 9 4,5	780 270 315	750 200 300	900 300 350
Итого:	130	-	160	-	1365	1250	1550

Рассчитаем индекс цен: или 88,1%.

Существует другой способ расчета индекса цен; в этом случае соизмерителем выступает объемный показатель в базовом периоде – q_0. Тогда формула индекса цен будет иметь вид:

. Такой способ расчета индекса цен был предложен немецким экономистом Э. Ласпейресом, поэтому этот индекс носит его имя – индекс Ласпейреса.

Но вернемся к нашему примеру и определим, насколько изменился общий оборот турпродуктов в отчетном периоде по сравнению с базисным периодом:

или 109,2%

Для определения индекса общего оборота можно воспользоваться взаимосвязью индексов (мультипликативная модель индексов):

или 109,2%.

Таким образом, мы подтвердили взаимосвязь между индексами в относительном выражении, но связь между ними существует и абсолютном выражении. Она существует как разница между числителями и знаменателями индексов:

тыс. рублей;

тыс. рублей;

тыс. рублей.

Если сложим разницы числителей и знаменателей второго и третьего индексов, то получим:

300+ (-185)=115 тыс. рублей. Значит, можем констатировать влияние факторов (q и p) на общий оборот турпродуктов. Общее увеличение продаж турпродуктов в отчетном году по сравнению с базисным (160-130=30) повлекло за собой рост оборота на 300 тыс. рублей, а снижение цен на турпродукты в отчетном году по сравнению с базисным снизило оборот на 185 тыс. рублей.

Для определения сводных обобщающих показателей изменения исследуемых показателей используется средняя гармоническая форма общего индекса цен. В индексе цен Пааше знаменатель преобразован с помощью индивидуальных индексов цен и имеет форму:

.

Такое преобразование в отдельных случаях значительно упрощает расчеты, поскольку в знаменателе индекса цен Пааше имеется агрегат , где вместо подставляется

Рассмотрим ситуацию на примере фирмы, предоставляющей услуги в течение базисного и отчетного периодов:

Услуги	Индивидуальный индекс цен	Стоимость услуг в отчетном периоде (тыс. руб.)
А Б В	1,08 1,10 1,12	2400 600 1000
	-	4000

Тогда можно рассчитать индекс цен по Пааше:

или 109,3%. Объем услуг фирмы в отчетном периоде по сравнению с базисным периодом увеличился на 9,3%.

Блок 16. Индексы средних величин

Индексы переменного и постоянного состава, индекс структуры. На практике часто возникает необходимость измерении динамики средних величин и определении факторов, влияющих на саму динамику явления. Эти задачи решаются с помощью индексов переменного и постоянного (фиксированного) состава и индексов структурных сдвигов.

Индекс переменного состава - это соотношение средних величин признаков явления в отчетном и базисном периодах . В общем виде индекс переменного состава имеет следующий вид:

: .

Этот индекс называется индексом переменного состава, потому что средние величины меняются не только за счет индексируемого показателя, но и за счет изменения удельного веса (структуры) их в совокупности.

Индексы постоянного (фиксированного) состава отражают действие индексируемого фактора и показывают его влияние на изменение изучаемого признака. Строится этот индекс как отношение средних взвешенных величин при одной фиксированной структуре, что позволяет исключить влияние изменения структуры для двух периодов.

; В агрегатной форме этот индекс может быть представлен как:

Индексы структурных сдвигов определяют влияние изменения структуры изучаемой совокупности на динамику среднего уровня признака:

или в агрегатной форме .

Все эти индексы связаны между собой в следующую систему: или

Если в качестве весов используются удельные веса единиц в общей совокупности, то эти доли можно представить как:

Тогда, система индексов может быть представлена следующим образом:

С помощью этой системы индексов можно отразить абсолютное изменение среднего уровня признака за счет отдельных факторов.

Общий абсолютный (уменьшение) прирост среднего уровня признака находится как разность числителя и знаменателя индекса переменного состава:

Абсолютный прирост (уменьшение) среднего уровня признака за счет изменения значений признака у отдельных единиц совокупности определяется как разность числителя и знаменателя индекса постоянного (фиксированного) состава:

Абсолютный прирост (уменьшение) среднего уровня признака за счет структурных изменений рассчитывается как разница числителя и знаменателя индекса структурных сдвигов:

тогда в общем виде абсолютные приросты выглядят следующим образом:

Рассмотрим на примере возможности индексного анализа. Два отделения одной фирмы, действующие на рынке туриндустрии, с разным числом работников предоставляли услуги в отчетном и базисном году. Проанализируем, как повлияла производительность труда работников отделений на объем предоставляемых услуг:

Отделения	Объем услуг в базисном году (млн. руб.) Q0	Объем услуг в отчетном году (млн. руб.) Q1	Численность работников в базисном году f0	Численность работников в отчетном году f1
1 2	45 90	60 85	30 70	32 65
	135	145	100	97

Сначала определим производительность труда ( ) работников отделений в базисном и отчетном периодах:

1-е отделение

.

2-е отделение

Затем найдем среднюю производительность по двум отделениям в базисном и отчетном периоде:

Определим индекс переменного и постоянного (фиксированного) состава и индекс структурных сдвигов:

Проверим правильность соотношения 0,97=1,071:1,104.

Теперь можно определить абсолютный общий и частный прирост (уменьшение) признаков как разница числителей и знаменателей индексов:

млн. рублей; млн. рублей;

млн. рублей.

_{9,53=13,58+(-4,05).}

Итак, по работе двух отделений фирмы в отчетном и базисном году можно сделать следующий комментарий. Первое отделение за период увеличило объем услуг и численность работников. Второе отделение снизило объем услуг и численность своих работников. Производительность труда в среднем на одного работника в первом отделении увеличилась на 25%, а во втором – на 1,6%. В среднем по двум отделениям производительность труда увеличилась на 10,4%.

В целом по фирме прирост производительности труда одного работника в абсолютном выражении составил 0,1 млн. рублей, в том числе за счет роста производительности труда в отделениях на 0,14 млн. рублей и снизился на 0,04 млн. рублей за счет структурных изменений.

Модуль 7. Статистический анализ связей явлений

Блок 17. Виды связей явлений

Все явления объективного мира находятся в причинно-следственных связях и взаимно обусловлены. Познание социально-экономических явлений означает познание их во всех или определяющих связях и взаимозависимостях. Одной из основных задач статистики является установление причинно-следственных связей, действующих в общественных явлениях. Особенность связей в социально-экономических явлениях состоит в том, что их закономерный характер проявляется лишь в массе явлений.

Известно, что , т.е. результативный признак у является функцией от признака-фактора х и для того, чтобы воздействовать на у надо изменить х. Связи между признаками явлений и самими явлениями могут быть функциональными и корреляционными.

Функциональные – это такие связи, в которых каждому значению одного признака х на единицу соответствует изменение другого признака у на строго определенную величину. Например, увеличение радиуса окружности на 1 см. приводит всегда к увеличению длины окружности на 6,28 см., т. к. она определяется по формуле

Корреляционные – это такие связи, когда при одном и том же значении признака х имеют место различные значения признака у, при этом между ними существует соотношение, когда определенному изменению признака х соответствуют среднее изменение признака у.

По направлению принято различать две формы связи: прямую и обратную. Прямая связь, при которой с ростом признака-фактора, возрастают значения результативного признака. В том случае, когда с увеличением признака-фактора, значения результативного уменьшаются имеет место обратная связь.

По форме выражения различают прямолинейные и криволинейные связи. Прямолинейной называется связь, которая может быть выражена уравнением прямой. Связь, которая может быть выражена уравнением какой-либо кривой линией, называется криволинейной.

В ходе статистического анализа возникает необходимость определения степени тесноты связи результативного фактора от вариации признака-фактора. Зная тесноту связи между отдельными факторами можно отобрать среди прочих наиболее важные и существенные факторы и осечь те, которые несущественно влияют на результативный признак фактор.

Для оценки тесноты связи между факторами существуют различные показатели. Простейшим из них является коэффициент корреляции знаков – коэффициент Г. Фетнера. Расчет этого показателя осуществляется вычислением средних значений обоих признаков, а затем определяются знаки отклонения от средней для всех значений взаимосвязанных признаков. С- число совпадений знаков отклонений индивидуальных значений от средней, а Н – число несовпадений знаков. Коэффициент принимает значения от -1 до +1.Если коэффициент имеет знак плюс, то имеется прямая зависимость, если минус, то связь обратная. Чем ближе коэффициент к единице, тем теснее связь. Рассмотрим на примере расчет коэффициента Фетнера:

Срок службы основных фондов (лет) х	Затраты на ремонт основных фондов (млн. руб.) у	Знак отклонения от средней для х	Знак отклонения от средней для у	Совпадение знаков (С) и несовпадение знаков (Н)
1 2 3 4 5 6 7 8 9 10	0,5 0,7 0,7 1,1 0,8 1.0 0,6 1,2 1,4 1,5	- - - - - + + + + +	- - - + - + - + + +	С С С Н С С Н С С С
55	8,9

Средний срок службы основных фондов составит , а средние затраты на ремонт млн. рублей. В последней графе таблицы указаны совпадения и несовпадения знаков отклонений от средних. Подставим их в формулу Фетнера:

, Полученная величина свидетельствует о том, что между сроком службы основных фондов и затратами на их ремонт существует значительная прямая зависимость.

Еще один метод нахождения связи между факторами – методом корреляции рангов и, в частности, коэффициент корреляции рангов К. Спирмена . В основе этого метода лежит рассмотрение разности рангов значений признаков. Формула этого коэффициента:

где n- число сопоставляемых пар, d- разность между рангами (порядковыми номерами) в двух рядах. Также как и коэффициент Фетнера этот коэффициент может находится в пределах от -1 до +1.

На примере часовой заработной платы сотрудников фирмы с различным стажем работы рассмотрим применение коэффициента корреляции рангов Спирмена.

При наличии одинаковых вариантов в рядах распределения ранг для расчета берется как их среднее арифметическое:

Стаж работы х (лет)	Ранг по порядку	Часовая заработная плата у (руб.)	Ранг по порядку	Ранг х для расчета	Ранг у для расчета	d	d2
2 4 4 5 6 8 10 11 12 14	1 2 3 4 5 6 7 8 9 10	30 40 35 40 38 48 64 65 62 80	1 4 2 5 3 6 8 9 7 10	1 2,5 2,5 4 5 6 7 8 9 10	1 4,5 2 4,5 3 6 8 9 7 10	0 -2 0,5 -0,5 2 0 -1 -1 2 0	0 4 0,25 0,25 4 0 1 1 4 0

Между стажем и часовой заработной платой установлена тесная корреляционная зависимость.

Преимущество коэффициента рангов Спирмена заключается в том, что он может применяться при любой форме распределения и для любых признаков.