Вид одиночного осциллятора и основное динамическое уравнение

m – приведенная масса; с - коэффициент вязкого трения; k - жесткость пружины.

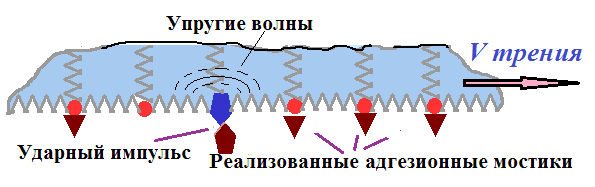
Для объяснения явления насыщения ВА сигнала при увеличении ФПК упругая система контактирующих пар была представлена в виде совокупности осцилляторов с различным набором динамических параметров (масса, жесткость, демпфирование), соответствующих исследуемому частотному диапазону. Жесткость осцилляторов определялась не только исходным значением, определяемым особенностями конструкции, состоянием поверхности и свойствами материала, но и наличием адгезионных мостиков, которые увеличивали жесткость всей динамической системы в окрестности контактирующих неровностей. Это уменьшает податливость осциллятора. Рисунок 8.

а

б

Рис. 8. Соударение неровностей: а – адгезионные мостики отсутствуют; б - адгезионные мостики возникли.

На рис. 9 показаны схемы осцилляторов, где адгезионные связи проявлялись в виде дополнительной жесткости. На основании такой упрощенной динамической модели можно проследить изменение ее АЧХ с ростом плотности адгезионных связей.

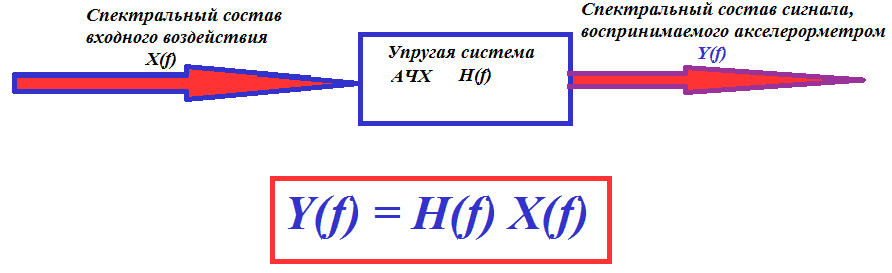
ВА энергия, возбуждаемая во фрикционном контакте, распространяется по упругой системе механизма, возбуждая колебания всех его элементов, включая и установленный акселерометр или другой датчик колебаний. Т.о., упругая система механизма является акустическим каналом, по которому информация из зоны трения или резания поступает к первичному преобразователю. В качестве модели акустического канала механизма можно взять набор гармонических осцилляторов, собственные частоты которых равны собственным частотам механизма. Их совместное колебание под действием отдельных ударов и определяет форму ВА сигнала. Для понимания работы акустического канала достаточно исследовать колебания одного из осцилляторов.

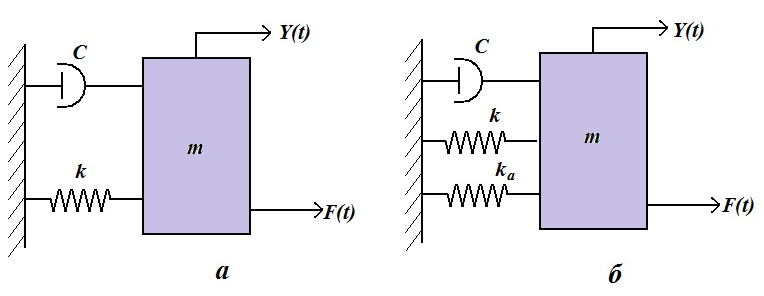
Рис. 9. Модель фрикционного контакта в условиях отсутствия адгезионных связей (а) и при их возникновении (б)

На рис 9 буквами k, c и m обозначены жесткость, демпфирование и масса соответственно, F(t) -возмущающая сила со стороны взаимодействующих неровностей, y(t)- перемещение, формирующее упругие волны, контролируемые первичным преобразователем.

Частотное представление динамической системы

Для представленной динамической модели изменение амплитуды y(t) в зависимости от частоты входного воздействия, задается амплитудно-частотной характеристикой H(f) в таком виде:

, (2.3.5)

где , .

Поскольку основной вклад в энергию сигнала осциллятор вносит на собственной частоте f_n, то выражение 2.3.5 рассматривается в окрестности собственной частоты (f = f_n):

. (2.3.6)

Поскольку энергия выходного сигнала пропорциональна квадрату амплитуды, то для дальнейшего рассмотрения возьмем квадрат выражения 2.3.6:

. (2.3.7)

Из 2.3.7 видно, что квадрат АЧХ обратно пропорционален жесткости осциллятора на резонансной частоте. Совокупность осцилляторов с разным набором динамических характеристик определяет АЧХ упругой системы, являющейся акустическим каналом.

Возникновение адгезионных мостиков на площади контакта меняет динамическую характеристику осциллятора. К изначально существующей жесткости упругой системы добавляется жесткость kа, определяемая адгезионными связями. Т.о., квадрат АЧХ акустического канала в окрестности какой-либо собственной частоты можно представить в виде:

, (2.3.8)

где константа определяет все остальные параметры, а k_Σ является суммарной жесткостью упругой системы рассматриваемого осциллятора и адгезионных мостиков, реализующих дополнительные связи осциллятора, появляющиеся на контактной площадке. Т.о., жесткость осциллятора в модели канала наблюдения может в первом приближении представляться так:

k_= k + k_а (2.3.9)

В выражении 2.3.9 величина k не меняется от условий контактирования, а k_а может меняться от 0 до больших значений в зависимости от прироста ФПК.

Если допустить, что адгезионные мостики распределены по площади контакта равномерно и их характеристики одинаковы, то становится очевидным предположение о пропорциональности kа площади и давлению в контакте. Появление kа на рис 9б отмечено появлением дополнительной жесткости. Из выражения 2.3.9 вытекает, что возможны две крайние ситуации: когда kа мало по сравнению с k и ее можно не учитывать, и наоборот, когда k мало по сравнению с kа и ее влияние становится малозначительным.

При увеличении площади или давления в подвижном контакте растет число ударных импульсов, пропорционально им растет число адгезионных мостиков, увеличивающих значение kа. Из выражения 2.3.1 следует, что мощность составляющих спектра входного воздействия увеличивается пропорционально частоте возмущающих импульсов. Тогда с учетом выражения 2.3.8 в упрощенном виде зависимость мощности ВА сигнала от частоты контактных взаимодействий может быть представлена выражением:

E = const f_возм / (k + k¹_а∙f_а) (***)

где f_возм – средняя частота соударений контактов отдельных неровностей, f_а – средняя частота возникновения адгезионных связей; ka¹ - средняя жесткость единичной адгезионной связи (допускается, что k_a(f)≈k¹_a∙f_а).

В условиях стационарного пересопряжения неровностей соотношение между f_возм и f_а приблизительно постоянно, а те и другие частоты пропорциональны частоте контактных взаимодействий f. При этом можно принять, что частота возмущающих воздействий f_возм = f.

Но в зависимости от разных условий (скорость трения, чистота поверхности, интенсивность возмущающих воздействий) частота образования адгезионных связей f_а может быть меньше f.

Таким образом, можно ввести коэффициент виброактивности контакта К_ВА:

f_возм/ f_a = К_ВА или f/f_a = К_ВА

С учетом сказанного (***) можно записать в таком виде:

E = const f / (k + k¹_а∙f/К_ВА) (****)

Из (****) следует, что при больших значениях f мощность ВА сигнала стремится к постоянному значению, поскольку первым слагаемым в знаменателе можно пренебречь, т. е. проявляется эффект насыщения.

При малых значениях f вторым слагаемым в знаменателе можно пренебречь, поскольку адгезионные мостики еще не формируются. Но при этом числитель меняется пропорционально росту частоты возмущающих импульсов. В результате получается линейное возрастание мощности ВА сигнала в начальные моменты роста ФПК. Длительность этого линейного участка зависит от конкретных условий реализации процесса трения, от величины К_ВА.

Чем больше К_ВА, тем дольше (при равномерном приращении площади контакта) сохраняется рост мощности ВА сигнала при увеличении ФПК.

При малых К_ВА устойчивые адгезионные мостики формируются раньше при нарастании площади, соответственно, и акустическое равновесие наступает раньше.

Рис. 10. Схема изменения мощности ВА сигнала с ростом ФПК при двух типах процессов: пропорциональное нарастание мощности (линия 1); акустическое равновесие с мощностью Ео (линия 2)

На рис. 10 схематично представлены графики изменения мощности ВА сигнала с ростом ФПК при двух типах процессов: при пропорциональном нарастании мощности (линия 1) и при возникновении явления акустического равновесия с уровнем мощности ВА сигнала Е₀ (линия 2). Зоны «А» и «В» показывают области существования двух типов переходных процессов: с превышением значений акустического равновесия (зона «А») и с плавным переходом (зона «В»). Точка пересечения линий 1 и 2 называется точкой бифуркаций (раздвоений). Она характеризуется значением ФПК, равным S_б. Начиная с этой точки, система как бы делает выбор между той или другой ветвью своего развития. Линия 3 показывает линейное нарастание потенциальной энергии в упругой системе за счет роста силы трения и увеличения упругих деформаций в макросистеме. Т.о., линия 1 характеризует акустическую модель фрикционного контакта как линейную: акустический канал, связывающий точки контактного взаимодействия с местом установки датчика на упругой системе, является линейным, допускающий рассмотрение отдельных контактных взаимодействий в виде независимых слагаемых. Линия 2 характеризует акустический канал как существенно нелинейную систему.

При S < S_б потенциальная энергия в упругой системе фактически не накапливается, поскольку возникающие адгезионные мостики, если и возникают, то на короткое время и не перекрывают друг друга. Потенциальная энергия переходит в колебательную, не успевая накопиться. При S > S_б адгезионные мостики существуют в процессе их рекомбинации. Одни мостики разрываются, другие возникают, но нет промежутков времени, когда они исчезают совсем. В результате потенциальная энергия растет с увеличением площади или глубины контакта. Если же при S > S_б по какой-то причине возникает одновременный (кооперативный) разрыв мостиков на площади контакта (нарушается соотношение частот возмущения и адгезионного взаимодействия в пользу частоты возмущения, соответственно, растет К_ВА), то потенциальная энергия релаксирует и частично переходит в колебательную энергию. В первом приближении можно считать, что при этом ВА энергия будет тем больше, чем больше было накоплено потенциальной энергии к моменту разрыва. При тотальном разрыве адгезионных мостиков (К_ВА=∞) происходит скачкообразный рост амплитуды ВА сигнала в широком диапазоне частот.

Естественно, что вероятность таких явлений при небольших превышениях S_б больше чем при значительных площадях контакта, где ситуация стабилизируется, но если уже такое случается, то выход потенциальной энергии сопровождается большим повышением мощности ВА сигнала и свидетельствует о каком-то нарушении в работе механизма или о поломке.

Необходимо учитывать, что на практике мгновенного разрыва всех мостиков не бывает. Всегда есть время переходного процесса, в течение которого происходит разрушение адгезионных связей. Это время определяется условиями конкретной ситуации, и оно в значительной степени определяет мощность и состав возникающего ВА сигнала.

Состояние акустического равновесия не может существовать при любом увеличении площади контакта, поскольку увеличивающаяся с ростом площади нагрузка может вызвать дополнительные деформации упругой системы, нарушение положения контактирующих тел в пространстве, привести к пластическому течению материалов или к возникновению автоколебаний.

Т.о., можно отметить двоякую роль фрикционного контакта, которую он играет в процессе генерации ВА энергии.

С одной стороны, удары микронеровностей, образующих контакт, являются возмущающим фактором, порождающим волновые процессы в упругой системе, формирующим ВА энергию и соответ ствующий сигнал. С другой стороны, взаимодействующие микронеровности за счет адгезионных связей стремятся стабилизировать контактирующие поверхности друг относительно друга в процессе рекомбинации ее адгезионных мостиков - постоянной смены контактирующих микронеровностей за счет процессов разрушения одних связей и образования новых.

В стадии акустического равновесия процесс соударения микронеровностей происходит в условиях, обеспечивающих их более высокую жесткость закрепления, что способствует увеличению возможностей пластической деформации неровностей с выделением повышенного количества тепла и уменьшению доли упругих деформаций, которые определяют количество ВА энергии, поступающей в упругую систему.

Сказанное можно пояснить на примере, хорошо знакомом каждому, кто пытался обработать напильником края тонкой металлической пластины, зажав ее в тиски. При большом вылете из тисков, т.е. при низкой жесткости, обработка пластины становится невозможной: напильник почти не снимает металл, при этом раздается визг и скрежет (выделяется большое количество ВА энергии), температура заготовки почти не повышается. При минимальном вылете процесс обработки идет совсем в другом режиме: шума почти нет металл снимается при каждом проходе напильника, а заготовка быстро нагревается, что свидетельствует о наличии пластических деформаций. На качественном уровне процессы, идущие во фрикционном контакте, очень похожи на описанный пример.