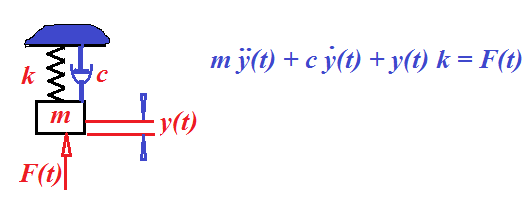Противоречия во взглядах на природу ва излучения при трении и резании

Изучение сил трения показало, что суммарная сила сопротивления в первом приближении равна сумме сил сопротивления , возникающих в единичных фрикционных связях, т.е.:

Эта формула отображает принцип аддитивности силы трения, который подтверждается экспериментальными и теоретическими исследованиями.

Опираясь на аддитивность силы трения и линейность канала наблюдения ВА сигнала, в большинстве работ, исследующих ВА процессы, было принято как очевидное без какой-либо проверки положение о пропорциональности мощности ВА сигнала количеству актов взаимодействия отдельных неровностей, участвующих в контактном процессе.

При трении двух поверхностей с постоянной скоростью увеличение количества взаимодействующих в единицу времени неровностей можно получить за счет увеличения силы нормального давления или за счет увеличения номинальной площади контакта. ФПК ( ), фактическая площадь контакта (рис. 4)), и действующая нормальная нагрузка (N) связаны соотношением:

,

где при пластическом контакте, а при упругом .

Поскольку, по данным той же работы, при увеличении нагрузки ФПК растет в основном за счет роста количества пятен контакта, то получается, что количество пятен контакта увеличивается почти пропорционально нормальной нагрузке. При постоянстве нормального давления на контактирующие поверхности увеличение номинальной площади контакта вызывает такое же увеличение ФПК и количества пятен контакта.

Если бы ВА сигнал подчинялся бы, как и сила трения, аддитивному закону, то при увеличении ФПК за счет роста давления в контакте или увеличения номинальной площади контакта наблюдалось бы пропорциональное увеличение мощности ВА сигнала (мощность сигнала пропорциональна квадрату его амплитуды).

Рис. 3.

На рис. 3 показаны примеры результатов экспериментальных проверок изменения уровня амплитуды виброускорения в различных частотных диапазонах при трении и резании в условиях изменения ФПК при контакте пластины из сплава Т15К6 со сталью 45. Видно, что при трении уровень ВА сигнала с какого-то момента достигает насыщения, и рост его прекращается. При резании эти зависимости носят более сложный характер, но хорошо видно, что быстрое нарастание амплитуды ВА сигнала происходит только при самых малых глубинах, а дальше это нарастание либо прекращается, либо происходит значительно медленнее.

Т.о., говорить о пропорциональности мощности ВА сигнала количеству пятен фактического контакта поверхности в общем случае нельзя. О линейном нарастании мощности ВА сигнала можно говорить только в диапазоне малых значений ФПК.

Практика применения методов ВА диагностики тоже говорит за то, что закономерности излучения акустических сигналов не столь просты как это допускается в теоретических предположениях.

Рис. 3. Примеры изменения уровня ВА сигнала от сближения (δ) контактирующих поверхностей, глубины резания (t), нормальной силы (N), ширины контакта (b).

3. Акустическая модель фрикционного контакта

При моделировании акустических свойств фрикционного контакта при сухом трении в основу было положено утверждение, что ВА сигналы возникают в результате силового (ударного) взаимодействия неровностей контактирующих тел. Удары могут возникать в моменты соприкосновения контрвыступов и в моменты их разъединения. На рис. 4 схематично показаны структурные компоненты реального контакта шероховатых поверхностей. Помимо номинальной площади контакта (А_а) в число компонентов на схеме показана контурная площадь контакта (А_с), на которой располагаются контактирующие выступы, формирующие реальную площадь контакта (А_r). Совокупность всех площадок реального контакта формирует площадь фактического контакта (ФПК). Поверхности твердых тел обладают свободной поверхностной энергией. Это обусловливает высокую активность поверхностных слоев, принимающих участие в трении. Таким образом, склонность твердых тел к схватыванию определяется их свободной поверхностной энергией (т. е. склонностью к адгезии) и их способностью пластически деформироваться. Последнее обстоятельство обеспечивает достаточное сближение поверхностей для возникновения адгезионных мостиков. При возникновении адгезионных мостиков сокращается свободная энергия поверхностей, система становится более устойчивой. Для разрыва мостиков требуется затратить энергию, часть которой пойдет на увеличение свободной поверхности. На рис. 5 показаны фазы взаимодействия неровностей. Часть из них находятся в состоянии образования адгезионных мостиков сварки, а другая часть находится в фазах соударения или в фазах разрыва связей. Соударение и разрыв взаимодействующих неровностей генерируют ВА энергию.

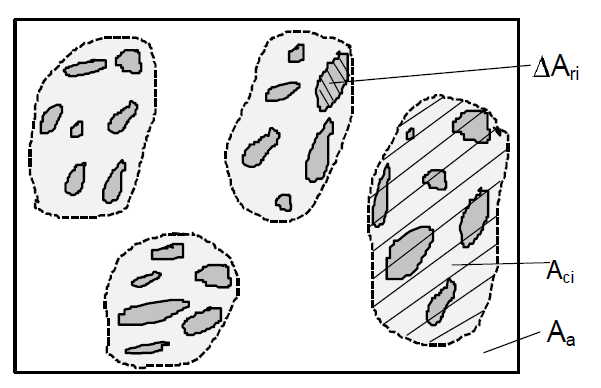
Рис. 4. Структурные компоненты реального контакта шероховатых поверхностей: А_а – номинальная площадь контакта; А_сi - контурная площадка; А_ri – фактическая площадь единичного пятна контакта.

Рис. 5. Схематичное представление элементарных процессов во фрикционном контакте: а, в – фаза образования адгезионных мостиков; б – фаза соударения неровностей при вступлении в контакт; г – фаза разрыва адгезионных мостиков

Построение моделей, описывающих поведение ВА сигнала во фрикционном контакте, основывается на предположении, что участки ФПК распределены равномерно по поверхности контакта, что при постоянстве давления в контакте среднее количество адгезионных мостиков и неровностей, генерирующих ВА энергию, постоянно.

Поскольку количественные изменения ФПК приводят к качественному изменению акустических свойств фрикционного контакта, то вполне естественно предположение, что количество акустической энергии, излучаемой при соударении отдельных неровностей, зависит от количества адгезионных мостиков окружающих точку соударения.

Явление насыщения энергии (также мощности и амплитуды) ВА излучения при росте ФПК за счет увеличения номинальной площади контакта или давления было названо «акустическим равновесием».

Рис. 6. Типичные кривые изменения мощности ВА излучения при росте ФПК

На рис. 6 показаны кривые, которые схематичным образом приближают наиболее часто встречающиеся переходные процессы изменения мощности (Е) акустического сигнала при росте ФПК от 0 до значений, при которых реализуется состояние акустического равновесия. Кривые 1 и 2 показывают наиболее типичные случаи изменения мощности ВА излучения, кривая 3 характеризует гипотетические изменения в соответствии с экспоненциальным законом. Кривая 1 характеризует сравнительно плавные переходные процессы, кривая 2 показывает переходные процессы, характеризующиеся всплеском мощности ВА излучения перед выходом на уровень насыщения. Гладкий вид кривых, описывающих переходные процессы, экспериментально может быть получен только при использовании соответствующего механизма сглаживания огибающих ВА сигнала, нивелирующего отдельные выбросы, обусловленные дискретностью контакта. В сглаженном виде переходные процессы характеризуются монотонным нарастанием ВА мощности при начальных приращениях ФПК, которое затем сменяется насыщением.

Явление насыщения или «акустического равновесия», как показали эксперименты, возникает в очень широком частотном диапазоне при трении самых разнообразных материалов, включая и металлы и полимеры, поэтому может считаться объективной закономерностью процесса фрикционного взаимодействия.

При этом нельзя считать, что состояние равновесия будет присутствовать при неограниченном росте ФПК. Рост сил трения создает дополнительные деформации в упругой системе, меняет направление и характер относительного движения в контакте. Вызывает рост потенциальной энергии в системе, делая ее менее устойчивой. Однако при стабильной кинематике движения контактирующих поверхностей эффект быстрого роста мощности ВА сигнала в начальный момент контакта, с последующим переходом в состояние насыщения обычно всегда присутствует.

Это позволило рассмотреть гипотезу о том, что наряду с процессами возбуждения ВА излучения присутствуют процессы поглощения этого излучения по всей номинальной площади контакта, проявляясь, естественно, только на ФПК. Приращение акустической мощности (DЕ) от увеличения ФПК на величину DS может быть описано уравнением:

DЕ = f_B(E) DS – f_n(E) DS, (2.3.1)

где f_B(E) и f_n(E) – функции от излучаемой мощности Е, определяющие количество дополнительно возбуждаемой или поглощаемой мощности соответственно на единицу дополнительной площади контакта.

Для определения конкретного вида этих функций можно акустическую мощность, изменяющуюся, например, в соответствии с кривой 1 на рис 2.3.3 аппроксимировать экспонентой 3, описываемой уравнением:

, (2.3.2)

где Е₀ и К – константы. Из выражения 2.3.2 можно выразить первую производную dE(S)/dS в следующем виде:

. (2.3.3)

Преобразуя выражение 2.3.3 к виду аналогичному 2.3.1, можно записать:

. (2.3.4)

Сопоставляя уравнение 2.3.1 и 2.3.4 можно сделать вывод, что, если возбуждаемая акустическая мощность пропорциональна площади контакта, то поглощаемая – пропорциональна произведению площади на величину выделяющейся акустической энергии.

Хотя описанная модель соответствует по выходным результатам экспериментальным данным, она содержит противоречие с физической сущностью изучаемого волнового процесса. Для существования такого механизма необходимо, чтобы имело место доминирование хотя бы в начальной фазе тангенциальных смещений при взаимодействии неровностей. Такой механизм должен работать непосредственно на фрикционном контакте. Это могло быть реальным, если бы ВА излучение не распространялось от места возникновения во все стороны по объему окружающего материала. В этих условиях объяснить полное поглощение приращений акустической энергии, начиная с какого-то момента, не представляется возможным и требует уточнения акустической модели фрикционного контакта.

Чтобы показать отличие независимых контактных взаимодействий от тех результатов, которые фиксировались во фрикционном контакте, был поставлен специальный эксперимент, где независимый контакт моделировался падающими песчинками (см. рис. 7). Емкость с сухим кварцевым песком, имеющая в своем днище длинную прямоугольную щель с постоянной скоростью перемещалась над металлической пластиной с закрепленным на ней акселерометром. Пластина имела наклон, чтобы упавшие песчинки на ней не задерживались. Струя песка, сыпавшаяся из емкости с постоянной скоростью, надвигалась на пластину, увеличивая площадь проекции прямоугольной щели на пластину. Соответственно количество падающих в единицу времени песчинок увеличивалась пропорционально площади проекции. Мощность ВА сигнала, как показано на графике в верхнем углу рисунка, в этом случае увеличивалась пропорционально ширине l струи песка, т е. времени движения емкости с песком в данном эксперименте. Поскольку мощность ВА сигнала пропорциональна квадрату амплитуды, то рост амплитуды в высокочастотных диапазонах приближался к параболической зависимости от ширины l. Удар каждой песчинки о пластину можно рассматривать как имитацию соударения двух неровностей. Независимость ударов отдельных песчинок была обеспечена самими условиями эксперимента. Результат эксперимента доказывает, что при независимости входного воздействия со стороны отдельных импульсов мощность результирующего ВА сигнала практически соответствует аддитивному закону.

Из этого следует, что искажение аддитивного закона в экспериментах с реальным контактом поверхностей вызвано образованием и последующим разрушением адгезионных мостиков. Получается, что предположение о независимости друг от друга процессов, происходящих при взаимодействии отдельных неровностей, неправильное.

Пока ФПК мала соударения неровностей происходят без влияния адгезионных мостиков, мощность ВА сигнала возрастает по линейному закону. С увеличением плотности контакта растет частота взаимодействия неровностей, но начинают формироваться адгезионные мостики, нарушающие линейный закон увеличения мощности, приводя в дальнейшем всю систему в состояние насыщения (см. кривую 1 на рис. 6).

Рис. 7. Схема эксперимента, имитирующего независимые контакты неровностей: 1 – емкость с кварцевым песком; 2 – поток песка из прямоугольной щели; 3 – упругая пластина; 4 – акселерометр

Показанный на кривой 2 (рис.6) выброс амплитуды огибающей ВА сигнала объясняется дискретностью фрикционного контакта. При высокой чистоте поверхностей адгезионные контакты возникают раньше по отношению к грубым поверхностям, приближая переходный процесс к экспоненциальному виду. Наоборот, грубые поверхности не образуют адгезионных мостиков при бόльших значениях S. Это объясняется тем, что удары относительно крупных неровностей легко разрушают появляющиеся немногочисленные адгезионные мостики на поверхности контакта. Поэтому линейное нарастание мощности ВА сигнала происходит до тех пор, пока количество образующихся адгезионных мостиков не станет достаточным для противостояния ударам отдельных крупных неровностей. С этого момента ВА мощность падает, опускаясь до уровня акустического равновесия.