
- •У відповідних розділах по кожній темі:
- •Мета та завдання курсу:
- •Умовні позначення
- •3 .1,3.2. Многогранники та їх площі. Анотація
- •Тема: Розв’язування задач на властивості призми та знаходження площі її поверхні.
- •Р озглянемо приклади Задача №1
- •Д оведення
- •Задача №2
- •Розв’язання
- •К онтрольні запитання
- •Тема: Розв’язування задач на властивості паралелепіпеда та знаходження площі його поверхні.
- •К онтрольні запитання
- •Контрольні запитання
- •3.3. Тіла обертання та їх властивості. Анотація
- •Тема: Розв’язування задач на властивості циліндра і конуса.
- •З адачі на знаходження елементів циліндра.
- •Задачі (на знаходження елементів циліндра)
- •Контрольні запитання
- •Задачі ( на знаходження елементів конуса)
- •Контрольні запитання
- •Тема: Розв’язування задач на властивості кулі і сфери.
- •Контрольні запитання
- •4.1, 4.2. Об’ єми геометричних тіл. Анотація
- •Тема: Обчислення об’єму призми і паралелепіпеда.
- •К онтрольні запитання
- •Тема: Обчислення об’єму піраміди
- •Р озглянемо приклад Задача
- •Контрольні запитання
- •Тема: Обчислення об’єму конуса
- •Контрольні запитання
- •Тема: Обчислення об’єму кулі
- •Контрольні запитання
- •4.1, 4.2. Об’ єми геометричних тіл. Анотація
- •Контрольні запитання
- •Основна
- •Додаткова
Задачі ( на знаходження елементів конуса)
Наведіть приклади побутових предметів, які мають форму конуса.
Намалюйте тіло, утворене обертанням прямокутного трикутника навколо:
катета;
гіпотенузи.
Знайдіть площу осьового перерізу тіла, утвореного обертанням рівностороннього трикутника навколо його сторони, якщо її довжина 2 дм.
Гіпотенуза рівнобедреного трикутника, яка дорівнює 30 см, точками К і Р розділена на три рівні частини. Знайдіть довжини кіл, які описують ці точки під час обертання трикутника навколо його катета.
Чи правильно, що з усіх перерізів конуса площинами, які проходять через вершину, найбільшу площу має осьовий переріз?
Доведіть, що з усіх перерізів конуса площинами які проходять через вершину, найбільший периметр має осьовий переріз.
Радіус основи конуса 3 м, висота 4 м. Знайдіть твірну.
Висота конуса дорівнює радіусу основи. Знайдіть кут при вершині осьового перерізу конуса.
Осьовий переріз конуса – рівносторонній трикутник із стороною 10см. Знайдіть радіус і висоту конуса.
Твірна конуса b нахилена до площини основи під кутом 30о. Знайдіть висоту.
Твірна конуса l нахилена до площини основи під кутом α. Знайдіть:
висоту конуса;
радіус основи конуса;
площу основи;
площу осьового перерізу;
відстань від центра основи конуса до твірної.
Радіус основи конуса дорівнює 28 см, а твірна довжина висоти на 8 см. Знайдіть площу осьового перерізу конуса.
У конусі радіус і висота відповідно дорівнюють 6 см та 8 см. Знайдіть:
твірну конуса;
площу осьового перерізу;
площу основи конуса;
кут між твірною і висотою;
відстань від центра основи до твірної конуса.
Черездві твірні конуса проведено площину. Довжина хорди АВ дорівнює 10см. Твірна і висота конуса відповідно дорівнюють:
1) 13 см і 5 см;
2) 17 см і 15 см.
Знайдіть:
радіус основи;
площу осьового перерізу;
відстань від центра основи до хорди АВ;
висоту SC перерізу конуса;
площу перерізу конуса.
Радіуси основ зрізаного конуса 3 м і 6 м, висота 4 м. Знайдіть твірну.
Радіуси основ зрізаного конуса R і r, твірна нахилена до основи під кутом 45о. Знайдіть висоту.
Радіуси основ зрізаного конуса 3 дм і 7 дм, твірна 5 дм. Знайдіть площу осьового перерізу.
Контрольні запитання
Дайте означення прямого кутового конуса ( вершина, твірна, основа, висота, вісь, осьовий переріз конуса).
Що є осьовим перерізом конуса?
Що є перерізом конуса площиною, яка паралельна основі?
Що є перерізом конуса площиною, яка проходить через дві твірні?
Що таке зрізаний конус?
Тема: Розв’язування задач на властивості кулі і сфери.
Мета заняття: формування вмінь студентів знаходити невідомі елементи кулі (сфери) й визначити взаємне розміщення площини і кулі (сфери) у просторі.
СФЕРА. КУЛЯ.
|
|||
|
Сферою називається множина всіх точок простору, що знаходиться на даній відстані R від заданої точки О.
Кулею називається множина всіх точок простору, що знаходяться від заданої точки О на відстані, не більше за дану відстань R.
Сфера є поверхнею кулі.
|
||
ЧАСТИНИ КУЛІ
|
|||
Сегмент
Рис. 19 |
Рис. 20 |
Рис. 21 |
|
Р ОЗГЛЯНЕМО ПРИКЛАДИ
Задача №1
Радіуси куль дорівнюють 25 дм і 29 дм, а відстань між їх центрами 36 дм. Знайдіть довжину лінії, по якій перетинаються їх поверхні.
Р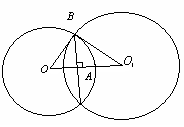 озв’язання
озв’язання
Розглянемо переріз, який проведемо через центри куль. Кулі перетинаються по колу радіусом АВ. АВ – висота BOO1. Площа трикутника дорівнює:
![]() ,
звідки
,
звідки
![]() .
.
З
Рис. 22![]() (дм2)
(дм2)
Визначимо АВ:
![]() (дм).
Визначимо довжину лінії перетину куль:
(дм).
Визначимо довжину лінії перетину куль:
![]() (м).
(м).
l = 4![]() м.
м.
Відповідь. 4 м.
Задача №2
Дано кулю радіуса R. Через одну точку її поверхні проведено дві площини: перша – дотична до кулі, друга – під кутом 30 о до першої. Знайдіть площу перерізу.
 Розв’язання
Розв’язання
![]() (за умовою). ОМ – радіус, який проведено
в точку дотику, отже,
(за умовою). ОМ – радіус, який проведено
в точку дотику, отже,
![]() .
.
Тоді
![]()
Із
![]() можна
визначити радіус перерізу О1М:
можна
визначити радіус перерізу О1М:
![]()
![]()
В
Рис.23
![]()
Відповідь.
![]()
ЗАДАЧІ
Радіус кулі дорівнює см. Всередині чи поза кулею розміщена точка А, якщо вона віддалена:
від центра кулі на 1 см;
від центра кулі на 1,5 см;
від точки на поверхні кулі на 3 см?
Діаметр кулі 38 дм, а площина віддалена від її центра на 20 дм. Чи має ця площина з кулею спільні точки.
Скільки діаметрів можна провести через точку, взяту:
на поверхні кулі;
всередині кулі.
Точки А і В лежать на поверхні кулі радіуса 50 см. Знайдіть відстань від центра кулі до відрізка АВ, якщо довжина цього відрізка 80 см.
Знайдіть площу великого круга і довжину великого кола, якщо його радіус дорівнює 2 см.
Кулю радіуса 5 см перетнуто площиною на відстані 3 см від центра. Знайдіть площу перерізу.
Кулю перетнуто площиною на відстані 6 см від центра. Площа перерізу дорівнює 64 см2. Знайдіть радіус кулі.
Кулю радіуса 41 см перетнутли площиною. Площа перерізу дорівнює 1600 см2. На якій відстані від центра кулі проведено площину?
Радіус кулі дорівнює R. Знайдіть:
діаметр кулі;
довжину великого кола;
площу великого круга;
сторону правильного трикутника, вписаного у велике коло;
площу правильного трикутника вписаного у великий круг;
якщо: 1) R = 3 cм; 2) R = 2 дм.
Кулю перетнутого січною площиною на відстані 8 см від центра кулі. Радіус кулі дорівнює R. Знайдіть:
площу великого круга;
довжину великого кола;
радіус перерізу;
площу перерізу;
кут між радіусом перерізу і радіусом кулі, проведених в одну точку кола перерізу;
площу квадрата, вписаного в переріз;
якщо: 1) R = 10 см; 2) R = 17 см.
На поверхні кулі дано три точки. Прямолінійні відстані між ними 6 см, 8 см, 10 см. Радіус кулі 13 см. Знайдіть відстань від центра кулі до площини, яка проходить через ці точки.
Катети прямокутного трикутника дорівнюють 30 см і 40 см. На якій відстані від площини трикутника знаходяться центр сфери, яка має радіус 65 см і проходить через всі вершини трикутника?
Вершини прямокутника лежать на сфері радіуса 10 см. Знайдіть відстань від центра сфери до площини прямокутника, якщо діагональ прямокутника дорівнює 16 см.
Сторони трикутника 13 см, 14 см і 15 см. Знайдіть відстань від площини трикутника до центра кулі, яка дотикається до всіх сторін трикутника. Радіус кулі 5 см.
Діагоналі ромба 15 см і 20 см. Кульова поверхня дотикається до всіх його сторін. Радіус кулі 10 см. Знайдіть відстань від центра кулі до площини ромба.
Через дотичну до поверхні кулі проведено дві взаємо перпендикулярні площини, які перетинають кулю по кругах радіусів r1 i r2. Знайдіть радіус кулі R.
Радіуси куль дорівнюють 25 дм і 29 дм, а відстань між їх центрами 36 дм. Знайдіть довжину ліній, по якій перетинаються їх поверхні.
Відстані між центрами двох куль і радіуси цих куль відповідно дорівнюють d, r1 i r2. Знайдіть:
радіус круга, по якому перетинаються ці кулі;
відстань від цента більшої кулі до площини перетину цих куль;
відстань від центра меншої кулі до площини перетину цих куль;
довжину лінії, по якій перетинаються сфери даних куль;
площу фігури, по якій перетинаються поверхні цих куль;
якщо:
d = 4 см, r1=
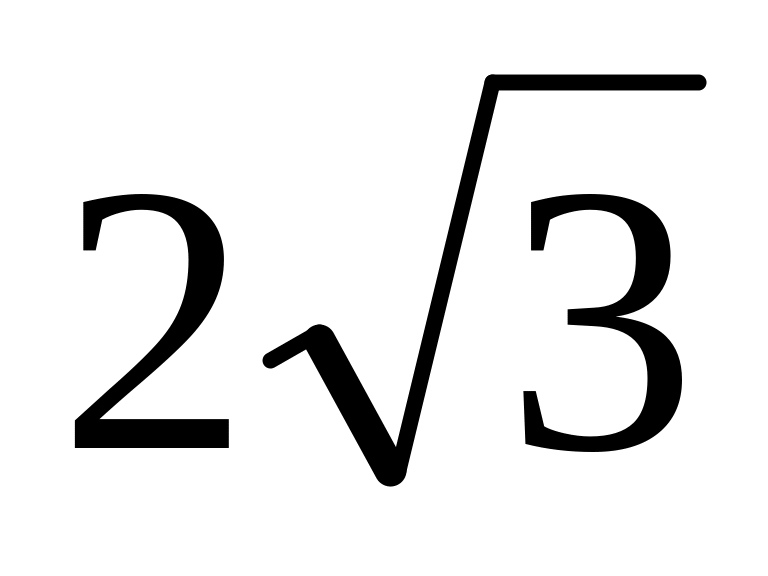 см,
r2
=
2
см;
см,
r2
=
2
см;d = 3 см, r1=
 см,
r2
=
см,
r2
=
 см.
см.
Через точку А поверхні кулі з центром в точці О проведене дотичну площину до кулі. У дотичній площині взято точку В. Відстань від точки А до точки В дорівнює 20 см, а радіус кулі – 15 см.
Знайдіть:
відстань від центра кулі до точки В;
площу великого круга;
кут нахилу прямої ОВ до дотичної площини;
величину кута АОВ;
площу трикутника АОВ.
Півкруг згорнули в конічну поверхню. Знайти кут між твірною і висотою конуса.

 Рис. 18
Рис. 18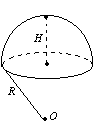
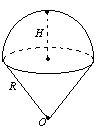 Сектор
Сектор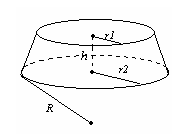 Зріз
Зріз