Контрольні запитання

1. Дайте означення піраміди (основи піраміди , бічних граней, ребер, висоти).

2. Бічні ребра піраміди рівні. У яку точку проектується її вершина?

3. Бічні грані піраміди однаково нахилені до основи. У яку точку основи проектується її вершина?

4. Скільки бічних граней, перпендикулярних до площини основи, може мати піраміда? Чим є спільне ребро цих граней?

5. Якою фігурою є переріз піраміди площинами, які проходять через її вершину, перпендикулярно до основи?

6. Що таке діагональний переріз піраміди? Якою фігурою є діагональний переріз? Чому?

7. Сформулюйте властивість площини, яка перетинає піраміду і паралельна основі піраміди.

8. Доведіть, що площина, яка перетинає піраміду і паралельна її основі, відтинає від неї подібну піраміду.

9. Що називається зрізаною пірамідою?

10. Яка піраміда називається правильною? Що таке вісь правильної піраміди?

11. Що таке апофема правильної піраміди?

12. Чому рівна бічна поверхня правильної піраміди? Доведіть це?

13. Який многогранник називається правильним?

14. Перелічіть п’ять типів правильних многогранників і опишіть їх.

3.3. Тіла обертання та їх властивості. Анотація

Розглядом найпростіших тіл обертання остаточно оформляється система основних геометричних фігур, які вивчаються в стереометрії: у розгляд вводяться циліндр, конус, куля і сфера. Одночасно з означенням конкретного тіла обертання студенти знайомляться з властивостями їх елементів, які потрібно буде зуміти правильно застосовувати в ході розв’язування геометричних задач.

На прикладах геометричних фігур, які вивчаються, вони знайомляться не тільки із загальними поняттями тіл обертання, а також розглядають питання взаємного розташування тіл обертання і площини: перерізи циліндра, конуса і кулі. Тому студентам потрібно повторити й систематизувати знання про взаємне розташування точок, прямих і площин у просторі, вимірювання відстаней і кутів у просторі, площі многокутників – тобто факти, відомі з предмету стереометрії.

З метою попередження можливих помилок при розв’язуванні задач слід підтримувати досить високий рівень обґрунтування висновків.

Література

[ 1, ст. 82 – 99]

[2, ст. 342 – 366]

[3, ст. 185 – 196]

[4, ст. 108 – 126]

[5, ст. 157 – 176]

Тема: Розв’язування задач на властивості циліндра і конуса.

Мета заняття: формування вмінь студентів знаходити невідомі елементи циліндра і конуса, використовуючи їх властивості.

План

1. З адачі на знаходження елементів циліндра.

2. Задачі на знаходження елементів конуса.

ЦИЛІНДР В Рис.15 ластивості Основи циліндра паралельні і рівні. Усі твірні рівні і паралельні між собою. Вісь, висота і твірні – перпендикулярні до основ.

К ОНУС В Рис.16 ластивості Усі твірні рівні між собою. Усі твірні нахилені до основи під однаковим кутом. Висота проходить через центр основи.

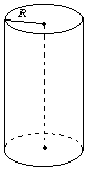
ЗРІЗАНИЙ КОНУС В Рис.17 ластивості Основи паралельні. Усі твірні рівні. Усі твірні нахилені до площини основи під однаковим кутом.

Р ОЗГЛЯНЕМО ПРИКЛАДИ

Задача №1

Осьовий переріз циліндра – квадрат, площа якого Q. Знайдіть площу основи циліндра.

Розв’язання

Сторона квадрата дорівнює Вона дорівнює діаметру основи. Тому площа основи дорівнює Відповідь. .

Задача №2

Радіус основи R. Осьовий переріз конуса – прямокутний трикутник. Знайдіть його площу.

Розв’язання

Прямокутний трикутник, який утворюється в перерізі, є рівнобедреним. Отже, висота конуса збігається з висотою трикутника і є водночас медіаною, тобто поділяє гіпотенузу трикутника навпіл. Гіпотенуза за умови дорівнює 2R. Відомо, що в рівнобедреному прямокутному трикутнику висота, яка опущена на гіпотенузу, дорівнює половині гіпотенузи. Отже, висота трикутника дорівнює R. Площа трикутника дорівнює: .

Відповідь. S = R².