- •У відповідних розділах по кожній темі:
- •Мета та завдання курсу:
- •Умовні позначення
- •3 .1,3.2. Многогранники та їх площі. Анотація
- •Тема: Розв’язування задач на властивості призми та знаходження площі її поверхні.
- •Р озглянемо приклади Задача №1
- •Д оведення
- •Задача №2
- •Розв’язання
- •К онтрольні запитання
- •Тема: Розв’язування задач на властивості паралелепіпеда та знаходження площі його поверхні.
- •К онтрольні запитання
- •Контрольні запитання
- •3.3. Тіла обертання та їх властивості. Анотація
- •Тема: Розв’язування задач на властивості циліндра і конуса.
- •З адачі на знаходження елементів циліндра.
- •Задачі (на знаходження елементів циліндра)
- •Контрольні запитання
- •Задачі ( на знаходження елементів конуса)
- •Контрольні запитання
- •Тема: Розв’язування задач на властивості кулі і сфери.
- •Контрольні запитання
- •4.1, 4.2. Об’ єми геометричних тіл. Анотація
- •Тема: Обчислення об’єму призми і паралелепіпеда.
- •К онтрольні запитання
- •Тема: Обчислення об’єму піраміди
- •Р озглянемо приклад Задача
- •Контрольні запитання
- •Тема: Обчислення об’єму конуса
- •Контрольні запитання
- •Тема: Обчислення об’єму кулі
- •Контрольні запитання
- •4.1, 4.2. Об’ єми геометричних тіл. Анотація
- •Контрольні запитання
- •Основна
- •Додаткова
К онтрольні запитання
Що таке двогранний кут (грань кута, ребро кута)?
Що таке лінійний кут двогранного кута?
Поясніть, що таке тригранний кут (грані і ребра тригранного кута).
Що таке многогранник?
Який многогранник називається опуклим?
Що таке грань опуклого многогранника, ребро, вершина?
Що таке призма ( основи призми, бічні грані, ребра)?
Призма має n граней. Який многокутник лежить в її основі?
Що таке висота призми?
Що таке діагональ призми, діагональні перерізи призми?
Сформулюйте властивість основ, бічних граней і бічних ребер призми.
Яка призма називається прямою, похилою, правильною?
Перелічіть властивості прямої і правильної призми.
Доведіть теорему про бічну поверхню призми.
Чому рівна площа повної поверхні призми?
Тема: Розв’язування задач на властивості паралелепіпеда та знаходження площі його поверхні.
М ета заняття: формування вмінь розпізнавати і знаходити елементи паралелепіпеда, використовуючи при цьому властивості граней, діагоналей паралелепіпеда, та знаходження площі його бічної і повної поверхні.
|
ПАРАЛЕЛЕПІПЕД Так називається призма, основи якої – паралелограми. Властивості: 1. Усі грані паралелепіпеда – паралелограми. 2. Протилежні грані паралельні і рівні. 3. Усі чотири діагоналі перетинаються в одній точці і точкою перетину діляться пополам. 4. Точка перетину діагоналей – центр симетрії. 5. Сума квадратів діагоналей дорівнює сумі квадратів усіх ребер:
|
|
Прямий паралелепіпед: паралелепіпед, бічні ребра якого перпендикулярні до основ. Властивості: 1. Бічні грані – прямокутники. 2. Основи – паралелограми |
Рис. 7 |
Прямокутний паралелепіпед: прямий паралелепіпед, основи якого – прямокутники. Властивості: 1. Усі чотири діагоналі рівні між собою. 2. Квадрат діагоналі дорівнює сумі квадратів ребер, що виходять з однієї вершини: d2=a2+b2+c2.
|
Рис. 8 |
Куб Властивості: 1. Усі грані – квадрати. 2. Усі ребра рівні між собою.
|
РОЗГЛЯНЕМО ПРИКЛАДИ
Задача №1
Доведіть, що в будь-якому паралелепіпеді сума квадратів діагоналей дорівнює сумі квадратів всіх його ребер.
Д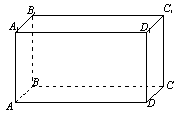 оведення
оведення
Нехай АВСDA1B1C1D1 – даний паралелепіпед. За властивістю діагоналей паралелограма маємо
для паралелограма AA1C1C:
![]() ;
;
для паралелограма BB1D1D:
![]()
![]() .
.
Додавши ці рівності почленно одержимо:
Рис. 9

Отже ,у будь-якому паралелепіпеді сума квадратів діагоналей дорівнює сумі квадратів всіх його ребер.
Задача №2
Основа похилого паралелепіпеда – квадрат із стороною а. Одна з вершин другої основи проектується в центр цього квадрата. Висота паралелепіпеда дорівнює Н. Знайдіть бічну поверхню паралелепіпеда.
Розв’язання
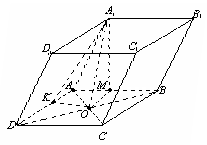
Нехай у паралелепіпеді ABCDA1B1C1D1
: ABCD – квадрат,
А1О
![]() (АВС),
точка О – центр квадрата, А1О
= Н, АВ = а.
(АВС),
точка О – центр квадрата, А1О
= Н, АВ = а.
Проведемо ОК АD, ОМ АВ; тоді А1К АD, А1М АВ ( за теоремою про три перпендикуляри), тобто А1К і А1М – висоти бічних граней ADD1A1 та ABB1A1 відповідно.
Рис.10![]()
![]() );
звідси:
А1К =
А1М.
);
звідси:
А1К =
А1М.
Оскільки AD
= AB i
A1K
= A1M,
то
![]() ,
тому
,
тому
![]() .
.
Із А
1ОМ
:
![]() .
.
Тоді
![]() .
.
Відповідь.
![]() .
.
ЗАДАЧІ
Паралелепіпед є чотирикутною призмою. Чи є правильним обернене твердження?
Чи існує паралелепіпед, що не є кубом, усі грані якого рівні між собою?
Чи є кубом паралелепіпед, у якого рівні між собою всі ребра і плоскі кути при одній з вершин?
Чи може перерізом прямокутного паралелепіпеда бути паралелограмом, що не є прямокутником?
Куб розрізами на 27 рівних кубиків. У скільки разів загальна площа поверхні отриманих кубиків більша за площу поверхні даного куба?
Як зміниться площа поверхні паралелепіпеда, якщо його виміри:
збільшити втричі;
зменшити вчетверо.
Три грані паралелепіпеда – прямокутники. Чи випливає з цього, що даний паралелепіпед прямокутний? Пояснити чому?
У паралелепіпеда три грані мають площі 1 м2, 2 м2 і 3 м2. Чому дорівнює повна поверхня паралелепіпеда?
Знайдіть виміри прямокутного паралелепіпеда, якщо площі трьох його граней 42 см2, 72 см2 і 84 см2.
Дано паралелепіпед, кожна грань якого – ромб із стороною а і кутом α. Знайдіть площу його поверхні.
Доведіть, що відрізок, який сполучає центри основ паралелепіпеда, паралельний бічним ребрам.
У прямому паралелепіпеді сторони основи 6 м і 8 м утворюють кут 300; бічне ребро дорівнює 5 м. Знайдіть повну поверхню цього паралелепіпеда
У прямому паралелепіпеді сторони основи 3 см і 8 см, кут між ними 600. Бічна поверхня дорівнює 220 см2. Знайдіть повну поверхню.
У прямому паралелепіпеді сторони основи 3 см і 5 см, а одна з діагоналей основи 4 см. Знайдіть більшу діагональ паралелепіпеда, знаючи, що менша діагональ утворює з площиною основи кут 600.
Знайдіть діагоналі прямого паралелепіпеда, кожне ребро якого дорів-нює а, а один з кутів основи дорівнює 600.
Бічне ребро прямого паралелепіпеда дорівнює 5 м, сторони основи дорівнюють 6 м і 8 м, а одна з діагоналей основи дорівнює 12 м. Знайдіть діагоналі ромба.
У прямому паралелепіпеді бічне ребро дорівнює 1 м, сторони основи дорівнюють 23 дм і 11 дм, а діагоналі основи відносяться як 2 : 3. Знайдіть площі діагональних перерізів.
Знайдіть діагоналі прямокутного паралелепіпеда за трьома його вимірами: а) 1, 2, 2; б) 2, 3, 6; в) 6, 6, 7.
У прямокутному паралелепіпеді сторони основи 7 дм і 24 дм, а висота паралелепіпеда 8 дм. Знайдіть площу діагонального перерізу.
Знайдіть третій вимір прямокутного паралелепіпеда, якщо два його виміри дорівнюють 6 см і 7 см, а діагональ паралелепіпеда дорівнює 11см.
Виміри прямокутного паралелепіпеда дорівнюють 3 см, 2 см і 6 см. Знайдіть:
довжину діагоналі паралелепіпеда;
довжину діагоналі найменшої грані;
площу найбільшої грані;
площу найменшої грані;
площу поверхні паралелепіпеда.
У прямокутному паралелепіпеді сторони основи дорівнюють a i b. Діагональ паралелепіпеда утворює з площиною основи кут α. Знайдіть бічне ребро.
У прямокутному паралелепіпеді діагональ d утворює з площиною основи кут α, а з бічною гранею -- кут β. Знайдіть виміри паралелепіпеда.
Знайдіть поверхню прямокутного паралелепіпеда за трьома його вимірами: 10 см, 22 см, 16 см.
Знайдіть бічну поверхню прямокутного паралелепіпеда, якщо його висота h, площа основи Q, площа діагонального перерізу М.

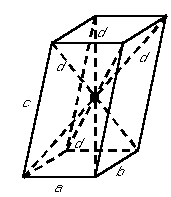 Рис. 5
Рис. 5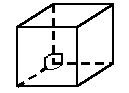 Рис. 6
Рис. 6