- •У відповідних розділах по кожній темі:
- •Мета та завдання курсу:
- •Умовні позначення
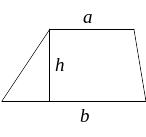
- •3 .1,3.2. Многогранники та їх площі. Анотація
- •Тема: Розв’язування задач на властивості призми та знаходження площі її поверхні.
- •Р озглянемо приклади Задача №1
- •Д оведення
- •Задача №2
- •Розв’язання
- •К онтрольні запитання
- •Тема: Розв’язування задач на властивості паралелепіпеда та знаходження площі його поверхні.
- •К онтрольні запитання
- •Контрольні запитання
- •3.3. Тіла обертання та їх властивості. Анотація
- •Тема: Розв’язування задач на властивості циліндра і конуса.
- •З адачі на знаходження елементів циліндра.
- •Задачі (на знаходження елементів циліндра)
- •Контрольні запитання
- •Задачі ( на знаходження елементів конуса)
- •Контрольні запитання
- •Тема: Розв’язування задач на властивості кулі і сфери.
- •Контрольні запитання
- •4.1, 4.2. Об’ єми геометричних тіл. Анотація
- •Тема: Обчислення об’єму призми і паралелепіпеда.
- •К онтрольні запитання
- •Тема: Обчислення об’єму піраміди
- •Р озглянемо приклад Задача
- •Контрольні запитання
- •Тема: Обчислення об’єму конуса
- •Контрольні запитання
- •Тема: Обчислення об’єму кулі
- •Контрольні запитання
- •4.1, 4.2. Об’ єми геометричних тіл. Анотація
- •Контрольні запитання
- •Основна
- •Додаткова
Контрольні запитання
Що таке куля (сфера)?
Що таке радіус і діаметр сфери?
Яка площа називається діаметральною площиною кулі? Що таке великий круг?
Що таке сегмент, сектор?
За якою формулою обчислюють площу сфери, сегмента?


ДОДАТОК 1
СПІВВІДНОШЕННЯ МІЖ ЕЛЕМЕНТАМИ ПРЯМОКУТНОГО ТРИКУТНИКА
|
|
ÐC = 90°; а, b – катети; с – гіпотенуза, (с > a, b > a) ÐA = α; ÐВ = 90°- α.
а2
+
b2=c2 - теорема Піфагора
a =
c ×
sin α ; b
= c ×
cos α ; а
= b
×
tg α ; b
= a ×
сtg
α .
Синус
кута
дорівнює
відношенню протилежного катета до
гіпотенузи
; косинус
кута
дорівнює відношенню прилеглого
катета до гіпотенузи ; тангенс
кута
дорівнює відношенню протилежного
катета до прилеглого ; котангенс
кута
дорівнює відношенню прилеглого
катета до протилежного.
|
|
ÐC = 90°,
hc2
= ac
×
bc
a2
= c ×
ac
b2
= c ×
bc
D
ACD ~ D
ABC
D
CBD ~ D
ABC
D
ACD ~ D
CBD
|

ДОДАТОК 2
ВПИСАНЕ І ОПИСАНЕ КОЛО
|
|
|
Довільний трикутник
Центр вписаного кола – точка перетину бісектрис.
Радіус
вписаного
кола:
де
S
– площа трикутника,
|
|
Довільний трикутник
Центр описаного кола – точка перетину серединних перпендикулярів.
Радіус
описаного
кола :
де S – площа трикутника. |
|
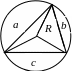
Прямокутний трикутник
Радіус вписаного кола:
|
a
c
b
R |
Прямокутний трикутник
Центр описаного кола співпадає з серединою гіпотенузи, а радіус дорівнює:
– половині
гіпотенузи
медіані,
проведеній до гіпотенузи
|
|
Рівносторонній трикутник
Центри вписаного і описаного кіл співпадають. Їх радіуси рівні:
Висота і площа:
|

ДОДАТОК 3
ПЛОЩА МНОГОКУТНИКА
|
Трикутник
|
П
|


ДОДАТОК 4
ПЛОЩА МНОГОКУТНИКА
|
|
Т
|
Довільнй многокутник
|

ДОДАТОК 5

По горизонталі: 1. Твердження, яке приймають без доведення. 3. Найбільша хорда кола. 5. Тіло, утворене обертанням круга навколо осі. 6. Латинська буква. 7. Елемент многокутника. 8. Перший. 9. Елемент кулі, сфери або кола.
Двадцятигранник. 13. Граничне положення січної. 14. Упорядкований запис числових даних. 15. Не означуване геометричне поняття. 17. Правильний чотирикутник. 19. Об’єднання просторової області і її поверхні. 20. Інша назва криволінійної трапеції. 21. Символ. 22. Одне з тіл обертання. 23. Бічна частина. 24. Поверхня кулі. 25. Відрізок у трикутнику. 26. Одна з тригонометричних функцій.
По вертикалі: 1. Давньогрецький математик. 2. Відрізок у правильній піраміді. 3. Давньогрецький математик. 4. Результат дії віднімання. 11. Площина, що проходить через віху і око спостерігача. 12. Математичний знак. 15. Інша назва многочлена. 16. Наука. 17. Український математик. 18. Одна з тригонометрич-них функцій.
Л ІТЕРАТУРА
ІТЕРАТУРА




 CD
= hc
– висота,
проведена до гіпотенузи с
CD
= hc
– висота,
проведена до гіпотенузи с


















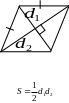
 аралелограм
аралелограм


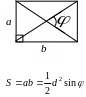 Ромб
Прямокутник
Квадрат
Ромб
Прямокутник
Квадрат