Контрольні запитання

1. Що таке куля?

2. Що таке радіус кулі, діаметр кулі? Які точки кулі називаються діаметрально протилежними?

3. Що таке сегмент, сектор?

4. Що таке великий круг?

5. Запишіть формулу для знаходження об’єму кулі, сегмента, сектора.

4.1, 4.2. Об’ єми геометричних тіл. Анотація

Поняття площі поверхні тіл обертання вводиться з опорою на наочне уявлення студентів.

В ході розв’язування задач на знаходження площі поверхні тіл обертання від студентів вимагається не тільки безпосереднє застосування вивчених формул, а й:

моделювання об’єктів навколишнього середовища за допомогою геометричних фігур і відношень між ними, тобто представлення їх за допомогою геометричних конструкцій і відношень між ними;

розпізнавання різних видів тіл обертання, їх елементів;

встановлення властивостей геометричних фігур шляхом вивчення перерізів, будови поверхні, виявлення симетрій;

побудови відповідних рисунків (перерізів, перетинів прямих і площин).

По-друге, студентам потрібно повторити і систематизувати факти, відомі їм із курсу планіметрії і стереометрії. А при розв’язуванні задач слід обґрунтовувати свої висновки.

Література

[ 1, ст. 116 – 121]

[2, ст. 383 – 390]

[3, ст. 200 – 202, 205 – 207]

[4, ст. 111 – 123, 159 – 164]

[5, ст. 161 – 171, 207 – 212]

Тема: Обчислення площі поверхні циліндра

Мета заняття: формування вмінь знаходити площу поверхні циліндра.

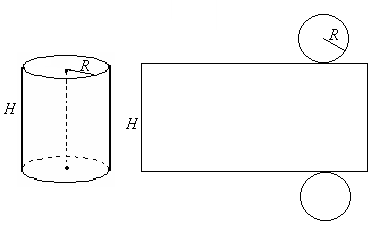
ЦИЛІНДР
Площа бічної поверхні
Площа повної поверхні
Об’єм

Р ОЗГЛЯНЕМО ПРИКЛАД

Задача

Циліндрична димова труба діаметром 65 см має висоту 18 м. Скільки жерсті треба для її виготовлення, якщо на заклепку іде 10% матеріалу?

Розв’язання

Бічна поверхня циліндра дорівнює: (м²).

На заклепку витрачається 10% матеріалу, тобто = 3,674 (м²).

Тоді на виготовлення труби необхідно така кількість жерсті:

S_o = S+ = 36,74 + 3,674 (м²).

Відповідь. 40,4 м².

ЗАДАЧІ

1. Чи призводить збільшення вдвічі радіуса основи прямого кругового циліндра до подвоєння площі його поверхні?

2. Площина, паралельна основі циліндра, поділяє його на рівновеликі циліндри. Чи рівними є між собою площі їх поверхонь?

3. Чи можна обчислити площу повної поверхні прямого кругового конуса, якщо відомі його висота і кут між твірною і висотою?

4. Чи є рівними між собою площі поверхонь тіл, утворених обертанням квадрата навколо його сторони і навколо його діагоналі?

5. Поверхня тіла, утвореного обертанням квадрата навколо сторони, рівновелика поверхні кулі, радіус якої дорівнює стороні квадрата. Доведіть.

6. Діаметр циліндра дорівнює 1 см, а висота дорівнює довжині кола основи. Знайдіть площу бічної поверхні циліндра.

7. Площа бічної поверхні циліндра дорівнює 15π см². Знайдіть площу осьового перерізу циліндра.

8. Осьовим перерізом циліндра є квадрат, площа якого дорівнює 16 см². Знайдіть повну поверхню циліндра.

9. Площа поверхні і площа бічної поверхні циліндра дорівнюють 50 см² і 30 см². Знайдіть радіус і висоту циліндра.

10. Висота конуса дорівнює Н, а діагональ осьового перерізу утворює з площиною основи кут 45^о. Знайдіть площу бічної і повної поверхні циліндра.

11. Напівциліндричне склепіння підвалу має 6 м довжини і 5,8 м у діаметрі. Знайдіть площу повної поверхні підвалу.

12. З круглого листа металу виштампували циліндричний стакан діаметром 25 см і висотою 50 см. Припустимо, що площа листа при штампуванні не змінилась. Знайдіть діаметр листа.

13. Радіус циліндра дорівнює r, а діагональ осьового перерізу – d. Знайдіть площу бічної поверхні і площу повної поверхні циліндра.

14. Радіус циліндра r, а висота h. Знайдіть довжину діагоналі осьового перерізу циліндра.

15. Радіус циліндра r, а діагональ осьового перерізу d. Знайдіть

    1. висоту циліндра;

    2. площу діагонального перерізу;

    3. площу бічної поверхні;

    4. площу поверхні циліндра.

16. Діагональ осьового перерізу циліндра дорівнює d і нахилена до площини основи під кутом α. Знайдіть:

1. висоту циліндра;

2. радіус циліндра;

3. площу бічної поверхні циліндра.

17. Осьові перерізи двох різних циліндрів – рівні прямокутники із сторонами 4 м і 6 м. Знайдіть площу поверхні того циліндра, у якого вона більша.

18. Висота циліндра дорівнює 16 см, радіус 10 см. Знайдіть площу його перерізу площиною, паралельною осі циліндра і віддалена від осі на 60 мм.

19. Радіус циліндра r, а висота h. Знайдіть площу перерізу циліндра площиною, яка перпендикулярна до основи і відтинає від кола основи дугу в 60^о.

20. Скільки квадратних метрів жерсті піде на виготовлення ринви довжиною 5 м і діаметром 20 см, якщо на шви додають 3% її площі.

21. Чи вистачить 8500 м² ізоляційної стрічки для двократного покриття нею кілометра газопроводу діаметром 1420 мм?

22. Практичне завдання. Зробіть із цупкого паперу розгортку циліндра.

К ОНТРОЛЬНІ ЗАПИТАННЯ

1. Що таке прямий круговий циліндр (твірна циліндра, основа циліндра, бічна поверхня циліндра, радіус циліндра, вісь циліндра, осьовий переріз циліндра)?

2. Які властивості мають основи і твірні циліндра?

3. Чому дорівнює площа основи циліндра?

4. Чому дорівнює площу бічної поверхні циліндра?

5. Чому дорівнює площа повної поверхні циліндра?

Тема: Обчислення площі поверхні конуса

Мета заняття: формування вмінь знаходити площу поверхні конуса

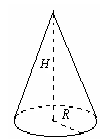
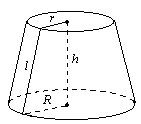
Рис. 34

	КОНУС	ЗРІЗАНИЙ КОНУС
Площа бічної поверхні
Площа повної поверхні
Об’єм

Р ОЗГЛЯНЕМО ПРИКЛАД

Задача

Площа основи конуса S, а твірні нахилені до основи під кутом . Знайдіть бічну поверхню конуса.

Розв’язання

В осьовому перерізі конуса лежить рівнобедрений трикутник SMN з кутом при основі. Бічна поверхня дорівнює: .

Радіус конуса визначимо, знаючи площу основи: ,

тоді . Твірну визначимо із : .

Бічна поверхня конуса дорівнює: .

Відповідь. .

ЗАДАЧІ

1. Нехай радіус основи прямого кругового конуса зменшеного вдвічі, а висоту збільшено вдвічі. Чи правильно, що площа бічної поверхні конуса не змінилась?

2. Чи поділяє осьовий переріз прямого кругового конуса навпіл площу його поверхні?

3. Чи можна обчислити площу повної поверхні прямого кругового конуса, якщо відомі його висота і кут між твірною і висотою?

4. Висота конуса дорівнює 6 см, радіус основи 8 см. Знайдіть бічну поверхню конуса.

5. Твірна конуса дорівнює 5 см, висота 4 см, зайдіть площу його повної поверхні.

6. Осьовий переріз конус – правильний трикутник, сторона якого дорівнює 6 см. Знайдіть бічну поверхню конуса.

7. Площа осьового перерізу конуса 0,6 см². Висота конуса дорівнює 1,2 см. Знайдіть площу повної поверхні конуса.

8. Площа основи конуса дорівнює 36 см², а його твірна – 10 см. Знайдіть площу бічної поверхні конуса.

9. Кут між твірною і віссю конуса дорівнює 45^о, а твірна – 6,5 см. Знайдіть площу бічної поверхні конуса.

10. Твірна конуса дорівнює 14 см, а кут при вершині осьового перерізу – 60^о. Знайдіть площу повної поверхні конуса.

11. Твірна конуса дорівнює 8 см і утворює з площиною основи кут 60^о. Знайдіть площу повної поверхні конуса.

12. Конусоподібну палатку висотою 3,5 м і діаметром основи 4 м покрито тканиною. Скільки квадратних метрів тканини пішло на палатку?

13. Дах силосної башти має форму конуса. Висота даху 2 м, діаметр башти 6 м. Знайдіть поверхню даху.

14. Як відносяться між собою бічна і повна поверхні рівностороннього конуса (у перерізі правильний трикутник)?

15. Знайдіть площу бічної поверхні зрізаного конуса, якщо радіуси основ дорівнюють 3 см і 6 см, а висота – 4 см.

16. Радіуси основ зрізаного конуса дорівнюють R i r (R > r), а твірна утворює з площиною більшої основи кут α. Знайдіть площу бічної поверхні зрізаного конуса.

17. У зрізаному конусі радіуси основ дорівнюють 6 см і 10 см, а твірна 5 см. Знайдіть радіус циліндра такої ж висоти, повна поверхня якого була б рівновелика повній поверхні зрізаного конуса.

18. У зрізаному конусі дано висоту Н, твірну l і бічну поверхню S. Знайдіть площу осьового перерізу.

19. Радіуси основ зрізаного конуса дорівнюють 3 дм і 6 дм, а твірна 5 дм. Знайдіть:

    1. висоту зрізаного конуса;

    2. площу осьового перерізу;

    3. кут нахилу твірної до площини основи.

20. Радіуси основ зрізаного конуса дорівнюють 5 см і 11 см, а твірна – 10 см. Знайдіть площі бічної і повної поверхні зрізаного конуса.

21. Скільки квадратних метрів латунного листа потрібно, щоб зробити рупор, у якого діаметр одного кінця 0,43 м, а другого – 0,036 м, а твірна 1,42 м?

22. Скільки оліфи треба, щоб пофарбувати зовнішню поверхню 100 однакових відер, які мають форму зрізаного конуса, якщо діаметри основ 25 см і 30 см, твірна 27,5 см і на 1 м² витрачають 150 г оліфи?

23. Практичне завдання. Зробіть із цупкого паперу розгортки конуса і зрізаного конуса.

КОНТРОЛЬНІ ЗАПИТАННЯ

1. Сформулюйте означення конуса. Назвіть його елементи.

2. Чому дорівнює бічна поверхня конуса?

3. Як обчислюють площу повної поверхні конуса?

4. Доведіть формулу для визначення площі поверхні конуса?

5. Що таке зрізаний конус? Назвіть його елементи.

6. Чому дорівнює площа бічної поверхні зрізаного конуса?

7. Запишіть формулу для знаходження площі повної поверхні зрізаного конуса.

Тема: Обчислення площі поверхні сфери

Мета заняття: формування вмінь студентів знаходити площу поверхні сфери.

	СФЕРА(КУЛЯ)	СЕГМЕНТ
Площа
Об’єм

Р ОЗГЛЯНЕМО ПРИКЛАД

Задача

Радіус кулі 15см. Яку площу має частина його поверхні, яку видно з точки, віддаленої від центра на 25см?

Р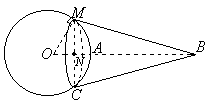 озв’язання

Н

Рис.36

еобхідно знайти площу кульового сегмента МАС. Висота сегмента Н = AN. МВ – дотична до кулі. Тоді (за властивістю дотичної). Отже, - прямокутний. Тоді виконується співвідношення: звідси (см).

Висота сегмента : H = AN = OA – ON = 6 (см).

Площа сегмента дорівнює: (см²).

Відповідь. см².

ЗАДАЧІ

1. Чи можуть рівновеликі кулі мати різні площі поверхонь?

2. Чи призводить збільшення вдвічі радіуса кулі до такого ж збільшення площі його поверхні?

3. Чи можна обчислити площу поверхні кулі, якщо відома площа перерізу, який знаходиться на заданій відстані від центра кулі?

4. Чи кожен переріз великого круга поділяє поверхню кулі на рівновеликі частини?

5. Знайдіть площу поверхні кулі, діаметр якої 10 см.

6. Площа великого круга кулі дорівнює 20π см². Знайдіть площу поверхні кулі.

7. Площа поверхні кулі дорівнює 64π см². Знайдіть діаметр кулі.

8. Довжина кола великого круга кулі дорівнює 10π см. Знайдіть площу поверхні кулі.

9. Дано півкулю радіуса R. Знайдіть її повну поверхню.

10. Вода покриває приблизно земної поверхні . Скільки квадратних кілометрів земної поверхні займає суша? (Радіус Землі вважати 6375 км).

11. У кулі проведено по різні сторони від центра два паралельні перерізи: площі перерізів дорівнюють 49π см² і 4π см², а відстань між ними 9 см. Знайдіть поверхню кулі.

12. Поверхня кулі дорівнює 144π см². Знайдіть об’єм кулі.

13. Об’єм кулі дорівнює 36π см³. Знайдіть поверхню кулі.

14. Чому дорівнює радіус кулі, якщо її поверхня (в см²) чисельно дорівнює об’єму кулі (в см³)?

15. У якому випадку витрачається більше матеріалу: на нікелювання однієї кулі діаметром 8 см чи на нікелювання 15 куль діаметром 2 см кожна?

16. Рівняння сфери Знайдіть її площу.

17. Точки A(2;0;3) і B(0;4;7) – кінці діаметра сфери. Знайдіть її площу.

18. Сфера з центром А(1;1;1) проходить через точку М(2;-1;8). Знайдіть площу сфери.

19. Радіус кулі дорівнює 6 см. На відстані 4 см від її центра проведено площину. Знайдіть:

    1. площу сфери;

    2. площу меншого сегмента;

    3. площу більшого сегмента.