Задачі на перпендикуляр і похилу.

1. З точки до площини проведено перпендикуляр і похилу довжиною

12 см. Знайти довжину перпендикуляра, якщо довжина проекції похилої дорівнює 7 см.

2. З точки до площини проведено перпендикуляр і похилу. Довжина проекції похилої дорівнює 6 см. Знайти довжини перпендикуляра і похилої, якщо кут між перпендикуляром і похилою дорівнює 30°.

3. З точки М до площини α проведено похилі МN і МК, а також перпендикуляр МF. Знайти МF і МК, якщо МN = 20 см, NF = 16 см,

КF = 5 см.

4. З точки М до площини α проведено похилі МК і МС і перпендикуляр МD. Знайти довжини похилих, якщо КD = 6 см, МСD = 30°,

МКD =60°.

5. З точки М до площини α проведено дві похилі МN і МК, довжини яких відносяться як 25 : 26. Знайти відстань від точки М до площини α, якщо довжини проекцій похилих МN і МК дорівнюють 14 см і 20 см.

6. Довести, що якщо проекції двох похилих, проведених до площини з однієї точки, рівні, то рівні і похилі.

7. В чотирикутнику АВСD: АВ = АD. Пряма SА перпендикулярна площині чотирикутника,  DSС =  ВSС. Довести, що ВС = СD.

8. З точки до площини проведено дві похилі, які дорівнюють 10 см і

17 см. Різниця проекцій цих похилих становить 9 см. Знайдіть проекції похилих.

9. В прямокутнику АВСD: АВ = 2 ВС. Пряма FВ перпендикулярна площині прямокутника, FВ = 7 см, FD = 12 см. Знайти сторони прямокутника.

10. З точки до площини проведено дві похилі. Знайдіть довжини похилих, якщо:

1. одна з них на 26 см більша від другої, а проекції похилих дорівнюють 12 см і 40 см;

2. похилі відносяться як 1:2, а проекції похилих дорівнюють

1см і 7 см.

Задачі на теорему про три перпендикуляри.

1. АВСDА₁B₁C₁D₁ – куб (рис. 11). Довести, що пряма АВ₁ перпендикулярна до прямих АD і В₁С₁.

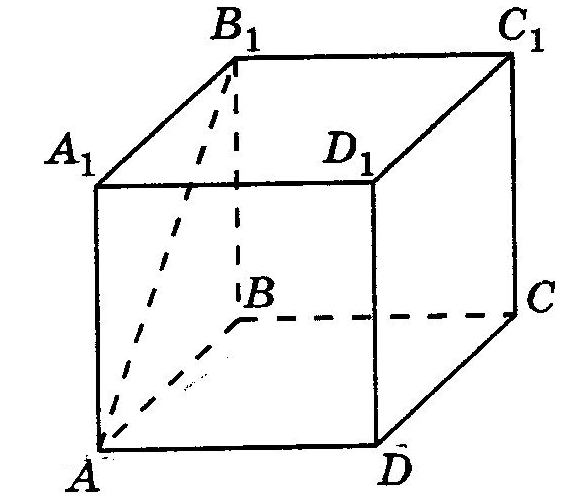
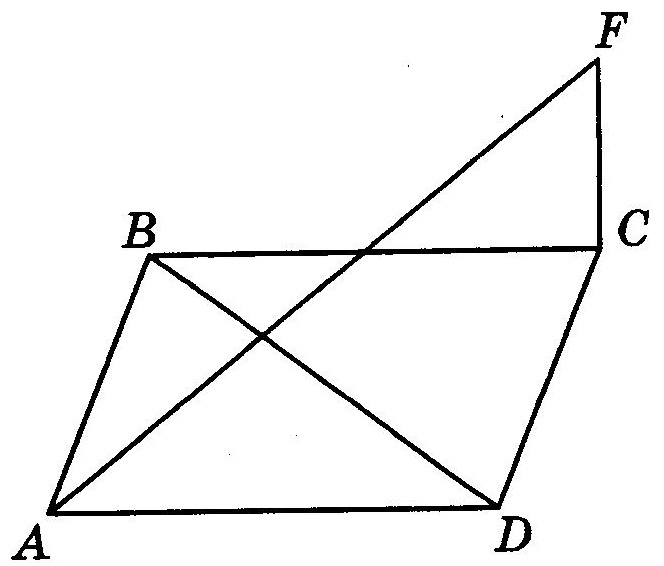
Рис. 11

Рис. 12

2. АВСD – ромб (рис. 12). Пряма FС перпендикулярна його площині. Довести, що прямі АF і ВD перпендикулярні.

3. До площини прямокутного трикутника АВС ( С = 90°) проведено перпендикуляр DA (рис. 13). Знайти відстань від точки D до точки В, якщо ВС = а, DС = b.

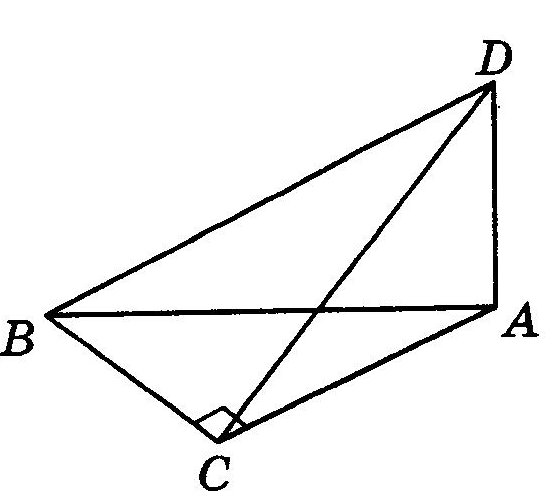
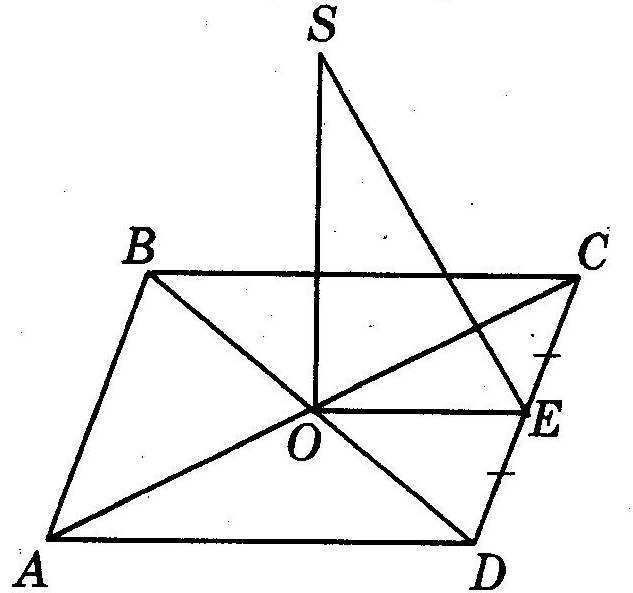
Рис. 13

Рис. 14

4. З точки О перетину діагоналей квадрата АВСD до його площини проведено перпендикуляр SО і точку S з’єднано з серединою сторони DС (рис. 14). Знайти довжину відрізка SС, якщо АВ = 8 см, SЕО = 60°.

5. З вершини прямого кута С трикутника АВС до його площини проведено перпендикуляр СМ довжиною 4 см. Знайти відстань від точки М до АВ, якщо АС = ВС = 8 см.

6. З вершини прямого кута С трикутника АВС до його площини проведено перпендикуляр СК. Відстань від точки К до прямої АВ дорівнює 13 см. Знайти відстань від точки К до площини трикутника, якщо його катети дорівнюють 15 см і 20 см.

7. З центра О кола, вписаного в правильний трикутник з стороною 6 см, до площини трикутника проведено перпендикуляр ОМ довжиною 3 см. Знайти відстань від точки М до сторін трикутника.

8. Основи рівнобічної трапеції дорівнюють 8 см і 18 см. З центра кола, вписаного в цю трапецію, до її площини проведено перпендикуляр ОМ. Точка М знаходиться на відстані 10 см від сторін трапеції. Знайти відстань від точки М до площини трапеції.

9. Діагоналі ромба дорівнюють 18 см і 24 см. Точка К знаходиться на відстані 3 см від площини ромба і рівновіддалена від його сторін. Знайти цю відстань.

10. У рівнобедреному трикутнику АВС: АВ = ВС = 17 см, АС = 16 см. Точка Р знаходиться на відстані 8 см від усіх сторін трикутника АВС. Знайти відстань від точки Р до площини трикутника.