
- •I частина
- •Тема 1.1 аксіоми стереометрії та найпростіші наслідки з них. Анотація
- •Площина визначається:
- •Взаємне розміщення прямої і площини:
- •З адачі на аксіоми стереометрії.
- •З адачі на перерізи.
- •Тема 1.2. Паралельність прямих і площин. Анотація
- •Паралельність прямої і площини.
- •Задачі на паралельність прямих.
- •Практичне заняття № 3 Задачі на паралельність площин.
- •Паралельність площин.
- •З адачі на паралельність площин.
- •Тема 1.3 перпендикулярність прямих і площин.
- •Тема 1.4. Перпендикуляр і похила. Анотація
- •Задачі на перпендикулярність прямої і площини.
- •Практичне заняття № 5 Задачі на перпендикулярність площин.
- •Перпендикулярність площин.
- •Задачі на перпендикулярність площин.
- •Практичне заняття № 6 Задачі на перпендикуляр і похилу.
- •Перпендикуляр і похила до площини.
- •Задачі на перпендикуляр і похилу.
- •Задачі на теорему про три перпендикуляри.
- •Тема 1.5 різні види кутів у просторі. Анотації
- •Задачі на кут між прямою і площиною.
- •Задачі на кут між площинами.
- •Задачі на площу ортогональної проекції многокутника.
- •Тема 2.1 прямокутні вектори і координати в просторі. Анотація
- •З адачі. Координати середини відрізка. Відстань між двома точками.
- •З адачі. Р івність векторів. Координати вектора. Колінеарність векторів.
- •З адачі. Скалярний добуток векторів. Кут між векторами.
- •Тема 2.2 рівняння площини і сфери Анотація
- •Задачі на рівняння площини.
- •Задачі на рівняння сфери
- •Співвідношення між елементами п a b c a b c α 90 - α рямокутного трикутника
- •Співвідношення між сторонами і кутами в довільному трикутнику
- •Квадрат
- •Площі трикутників
- •Основна
- •Додаткова
Співвідношення між елементами п a b c a b c α 90 - α рямокутного трикутника
C = 90; а, b – катети; с – гіпотенуза, (с > a, b > a)
а2 +
b2=c2
bc
ac
b
hc
C
sin α =
cos α =
tg α =
ctg α =
B
a
D
A
c![]() ;
;![]() ;
;![]() ;
;![]() .
.




 - теорема Піфагора
- теорема Піфагора
a = c
sin α ;
b = c
cos α;
а = b
tg α.
b = a
сtg
α.
C = 90
C
hc2
= ac
bc
a2
= c
ac
b2
= c
bc
ACD ~
ABC
CBD ~
ABC
ACD ~
CBD
Д ОДАТОК 3
Співвідношення між сторонами і кутами в довільному трикутнику

Теорема синусів :
![]()
R – радіус описаного кола
 Теорема
косинусів :
Теорема
косинусів :
c2
= a2
+ b2
– 2 ab cos γ ;
a2
= c2
+ b2
– 2 cb cos α ;
b2
= a2
+ c2
– 2 ac cos β .

НАСЛІДКИ
Якщо c2 = a2 + b2, то γ = 90˚, тобто трикутник прямокутний.
Якщо c2 < a2 + b2, то кут γ – гострий (cos γ > 0), тобто
трикутник гострокутний.
Якщо c2 > a2 + b2, то кут γ – гострий (cos γ < 0), тобто
трикутник тупокутний.
У трикутнику проти більшої сторони лежить більший кут,
проти більшого кута лежить більша сторона :
 a
> b
α
> β
a
> b
α
> β
Д ОДАТОК 4

П
a
a
S =
φ
d1
d2
половина добутку
діагоналей на синус кута між ними
φ
S =
d
d
b
a
S = ab
S =
a
d
d
S = a2
a
ПРЯМОКУТНИК
α
φ
h
d1
d2
b
S =
d1d2
sin φ
a
S = a
h
S = ab sin α
d2
d1
α
h
S =
d1d2
S = a
h
S = a2
sinα
РОМБ




![]() d1d2
sinφ
d1d2
sinφ






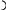
![]() d2
sin φ
d2
sin φ




![]() d2
d2
Квадрат







ПАРАЛЕЛОГРАМ
Д ОДАТОК 5

Площі трикутників
A
а
b
C
ha
c
а
b
S =
S =
ab sin
B
S =
60
60
60
а
а
а
S =
ab
S =
c
hc
S =
bc sinA
С
В
hc
с

![]() a
ha
a
ha


![]()

![]()





S =
![]()
![]()
S =
![]()
, де R – радіус описаного кола
S = r
p
, де r – радіус вписаного кола
ПРЯМОКУТНИЙ
ТРИКУТНИК

ПРАВИЛЬНИЙ ТРИКУТНИК
А

Д ОДАТОК 6
КРОСВОРД „Повторимо геометрію ”

По горизонталі: 6. Давньогрецький математик, який створив твір з математики під назвою „Начала”. 9. АВ – похила, АН – перпендикуляр до деякої прямої. Як називають відрізок ВН? 12. Фігура, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які попарно сполучають ці точки. 14. Відношення протилежного катета до прилеглого у прямокутному трикутнику. 15. Паралелограм, у якого всі сторони рівні. 16. Відношення протилежного катета до гіпотенузи у прямокутному трикутнику. 18. Твердження, яке доводиться. 20. Гіпотенуза прямокутного трикутника для кола, описаного навколо нього. 22. Твердження, яке не доводиться. 23. Фігура, яка складається з точки і двох різних променів, що виходять з цієї точки. 24. Фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. 25. Неозначуване поняття геометрії. 26. Трикутник зі сторонами 3, 4, 5. 27. Перпендикуляр, опущений з вершини трикутника на протилежну сторону.
По вертикалі: 1. Точка А у трикутнику АВС. 2. Промінь, який виходить з вершини кута, проходить між його сторонами та ділить навпіл. 3. Як називають формули виду sin (90 - )= cos тощо? 4. Сторона прямокутного трикутника, яка лежить навпроти прямого кута. 5. Медіана прямокутного трикутника, яка виходить з вершини прямого кута, для описаного навколо цього трикутника кола. 7. Давньогрецький учений, автор найвідомішої теореми й чемпіон олімпійських ігор з кулачного бою. 8. Відношення прилеглого катета до гіпотенузи у прямокутному трикутнику. 9. Розділ геометрії, в якому вивчаються властивості фігур на площині. 10. Відрізок прямої, перпендикулярної до даної прямої, який має одним зі своїх кінців точку перетину прямих. 11. Точка перетину перпендикуляра й прямої, до якої він проведений. 13. Сторона, прилегла до прямого кута прямокутного трикутника. 17. Одиниця вимірювання кутів. 19. Відрізок, що сполучає вершину трикутника з серединою протилежної сторони. 21. Відрізок АВ, не перпендикулярний до прямої а , де точка А не лежить на прямій а, а точка В лежить на ній.
Л ІТЕРАТУРА
ІТЕРАТУРА
