Проводимость определяется потерями за счет токов проводимости, а также потерями из-за поляризации диэлектрика или, иначе, диэлектрического гистерезиса.

Проводимость определяется потерями за счет магнитной вязкости ферромагнитного вещества или, иначе, магнитного гистерезиса . Вещества которые обладают одновременно электрическими и магнитными потерями, носят название бикомплексных.

ЭКРАНИРОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ.

Аналитический метод расчета эффективности экранирования основывается на решении уравнений Максвелла для гармонических колебаний.

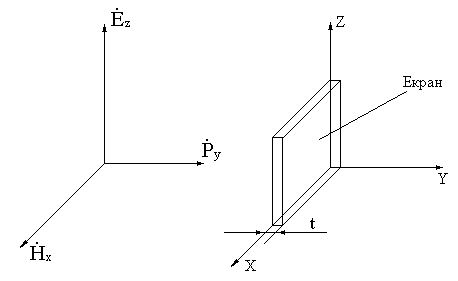
Рассматривают эффективность экранирования металлического экрана при нормальном падении на него плоской электромагнитной волны. Волна распространяется вдоль оси Y.

Считают экран линейной системой с большой протяженностью (последнее для исключения краевого эффекта). Случай нормального падения – это самый неблагоприятный. При наклонном падении электромагнитная волна частично отражается от стенки экрана (угол падения равен углу отражения, а преломленная волна практически распространяется в направлении нормали к границе – закон Снеллиуса).

Расчет сводится к определению составляющих электромагнитного поля, проникающего в экранированную область пространства (y  t), при известных параметрах воздействующего поля электрофизических и геометрических параметрах экрана (, , t) и электрофизических параметрах среды (_о, _о). Для рассматриваемого случая основные уравнения электродинамики имеют следующий вид:

Для диэлектрика области источника помех =0, =_о, =_о, решая систему уравнений, получают характеристическое сопротивление диэлектрика, которое для падающей и отраженной волны отличается лишь знаком, т. е. модуль характеристического сопротивления диэлектрика:

Токи проводимости в металле много больше токов смещения, т. е. . Решение

системы уравнений позволяет оценить характеристическое сопротивление металла, абсолютное значение которого:

Вводя коэффициент экранировки и решая систему уравнений для y  t, получают выражение для расчета коэффициента экранирования:

k – коэффициент распространения – волновое число в металле.

и коэффициента реакции экрана:

При этом эффективность экранирования:

В области низких частот:

Э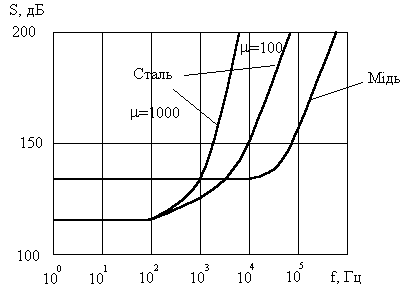 ффективность экранирования электромагнитного поля зависит как от материала, толщины экрана, так и частоты. С повышением частоты эффективность возрастает, причем эффективность экранов из магнитных материалов выше по сравнению с немагнитными, т. к. в области высоких частот появляется поглощение.

В табл. 1 приведены значения удельной проводимости на постоянном токе (статической удельной проводимости) глубины проникновения поля в металл, которая выражается формулой:

, (1)

а также величины

,

где – скорость света в вакууме.

Таблица 1

Электромагнитные характеристики некоторых металлов при температуре Т=20⁰ С

Металл
Серебро Ag	5,6	0,85	1,2	1,3	0,64	570	15
Медь Cu	5,2	0,92	1,2	1,4	0,66	420	14
Золото Au	3,8	1,3	1,4	1,6	0,78	410	16
Алюминий Al	3,2	1,5	1,5	1,8	0,84	150	10
Железо Fe	0,90	5,3	2,9	3,3	1,6	–	–

Из таблицы можно заключить, что все металлы при нормальном падении волн радио- и инфракрасного диапазонов имеют коэффициент отражения, практически не отличающийся от –1. Это означает, что фаза отраженной от металла электромагнитной волны сдвигается на .

Металлический слой. Пусть слой I – это металл, для которого а среды II и III – это воздух или вакуум. В таких условиях имеем ,

.

Выражения для коэффициентов отражения и прохождения при нормальном падении на металлический слой в следующей компактной форме

.

Эти выражения справедливы при условии , которое выполняется для всех металлов (см. табл. 1). Металлический слой называется толстым, если . В этом случае слой ведет себя как сплошной металл, поскольку волна, прошедшая внутрь металла, не доходит до второй границы раздела и полностью поглощается.

Металлический слой называют тонкой пленкой когда его толщина меньше глубины проникновения поля в сплошной металл. Для тонкой пленки, на первый взгляд, следовало бы ожидать резкого уменьшения коэффициента отражения. Однако более детальный анализ показывает что это не так и что пленки сохраняют почти идеальную отражательную способность вплоть до очень малых толщин, составляющих десятые и даже сотые доли толщины скин-слоя. Такое явление наблюдается при условии, если пленка плоская или слабоизогнутая. Если же радиус кривизны пленки сравним с длиной волны падающего поля, то коэффициент отражения резко падает. Для тонкой пленки при полагая гиперболические синусы равными своим аргументам, получаем

,

.

Заметим, что в эти выражения не входит частота. Этого и следовало ожидать, поскольку на всех частотах, для которых соблюдаются условия , поле равномерно по всей толщине пленки независимо от частоты. Можно показать , что

где – средняя длина свободного пробега электронов в металле.

Для поглощающего слоя целесообразно ввести еще и понятие коэффициента поглощения, равного отношению удельной поглощенной слоем энергии к удельной падающей на него энергии. Очевидно, что он равен

,

г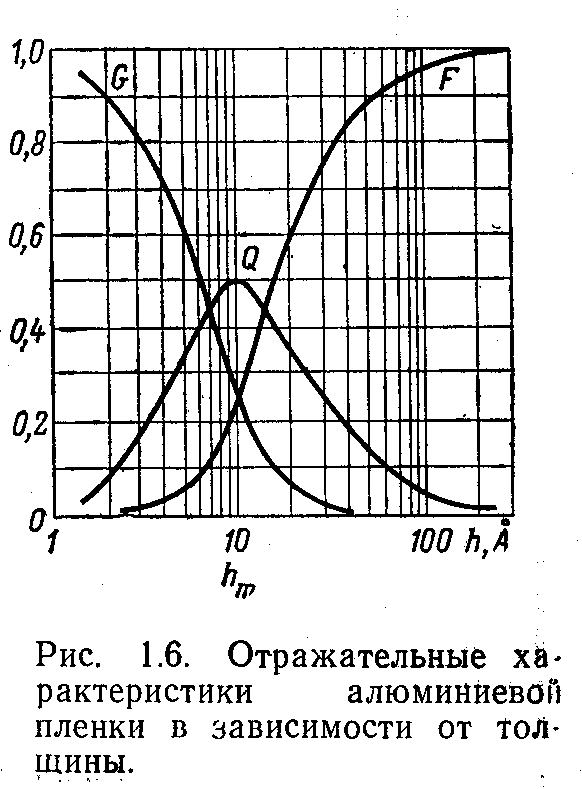 де – коэффициенты отражения и прохождения по мощности. Для тонкой пленки получаем полезные соотношения

.

Для алюминия, обладающего удельной проводимостью при . При толщина скин-слоя составляет . Коэффициент отражения при и при порядка , практически не отличается от –1. Даже при коэффициент отражения уменьшается незначительно и составляет . На рис. 1.6 представлена зависимость коэффициентов отражения, прохождения и поглощения по мощности от толщины алюминиевой пленки . Из графиков рис. 1.6 следует, что при некоторой толщине коэффициенты отражения и прохождения равны 0,25, а коэффициент поглощения достигает максимального значения 0,5.

ПЛОСКИЕ МЕТАЛЛИЧЕСКИЕ РЕШЕТКИ И СЕТКИ

Решеткой называют систему параллельных проводов или лент, расположенных вдоль плоскости на одинаковых расстояниях друг от друга (с постоянным шагом). Сеткой будем называть две решетки с взаимно перпендикулярными проводами, расположенными вдоль двух близких параллельных плоскостей.

Обратимся к простейшему случаю падения волны в направлении нормали к плоскости решетки. Коэффициент отражения мы определим как

где – комплексная амплитуда падающей волны в плоскости решетки, – комплексная амплитуда отраженной волны в дальней зоне, но пересчитанная в плоскость решетки.

Аналогично коэффициент прохождения мы определим как

где – комплексная амплитуда прошедшей волны в дальней зоне пересчитанная в плоскость решетки.

Кроме коэффициентов отражения и прохождения по напряженности поля и , в литературе часто используются коэффициенты отражения и прохождения по мощности (интенсивности), для которых имеем

Очевидно, что для решеток и сеток без потерь эти коэффициенты связаны соотношением

Все перечисленные коэффициенты зависят от поляризации поля. Введем понятия коэффициентов отражения и прохождения при параллельном и ортогональном приеме. Например, под будем понимать отношение компонент отраженного и падающего полей, поляризованных вдоль оси X, а под – отношение X- компоненты отраженного поля к Y-компоненте падающего поля.

Решетка из круглых стержней. Диаметр проводящих круглых стержней мал по сравнению с шагом решетки , т.е.

Пусть на решетку вдоль отрицательного направления оси Z падает плоская линейно-поляризованная волна. В случае так называемых индуктивных стержней, когда электрический вектор падающей волны параллелен стержням решетки , коэффициенты отражения . и прохождения . запишем в виде .

; .

. .

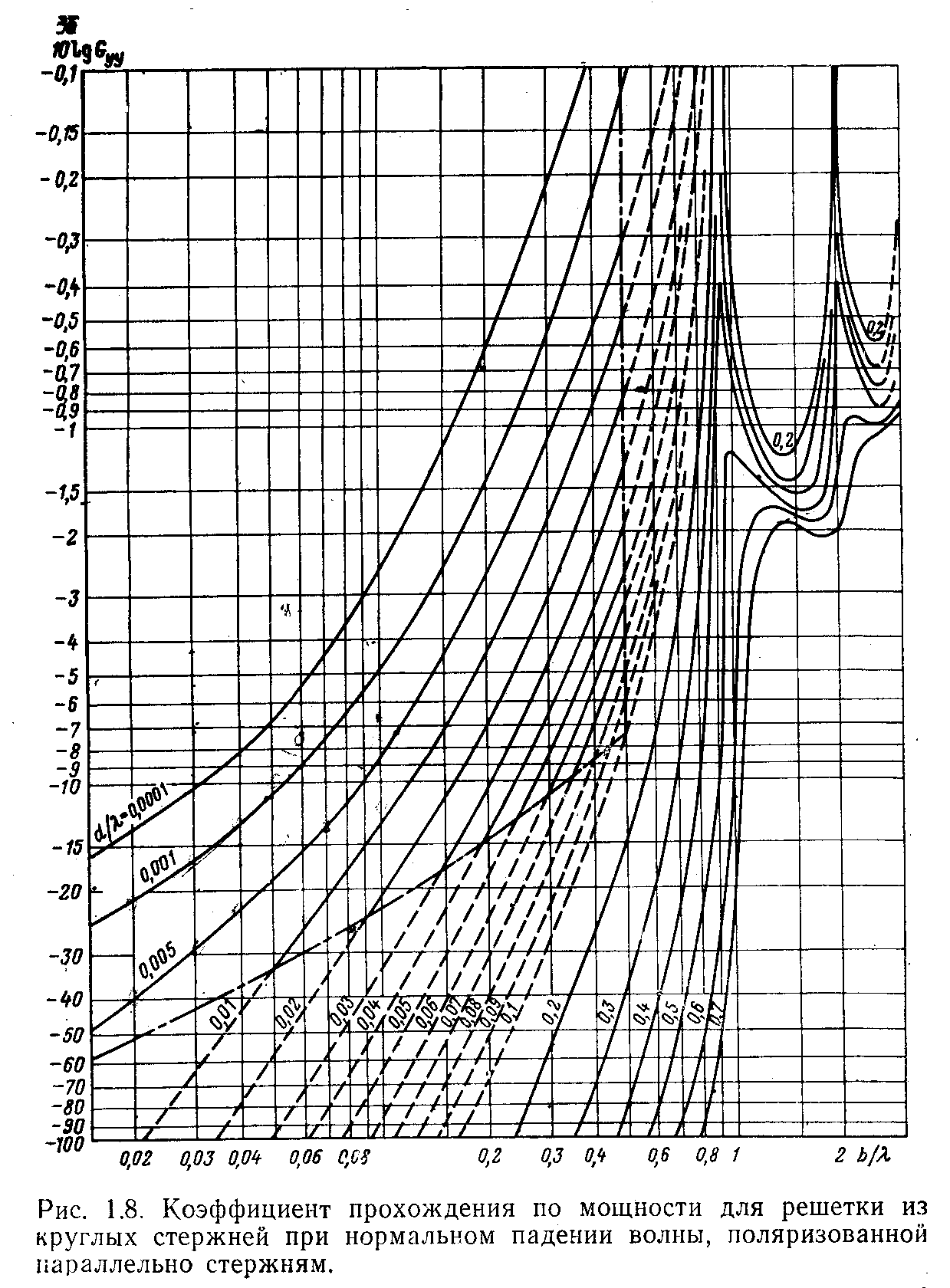
На рис. 1.8 представлена зависимость коэффициента прохождения по мощности от шага решетки и диаметра стержней . Для большей наглядности коэффициент прохождения отложен по оси ординат в логарифмическом масштабе. Область действия формулы располагается в верхнем левом углу графика. Ее границы отмечены штрихпунктиром. Пунктирные ветви кривых требуют уточнения, поскольку имеющиеся в литературе расчетные данные для этой области весьма скудны. Из графика видно, что индуктивная решетка, составленная их очень тонких стержней , пропускает около одного процента мощности при шаге порядка . Если шаг решетки приближается к длине волны, то коэффициент пропускания весьма быстро стремится к единице . С уменьшением шага решетки уменьшается коэффициент пропускания, причем .

В случае так называемых емкостных стержней, когда электрический вектор падающей волны перпендикулярен стержням решетки выражения для коэффициентов отражения и прохождения принимают вид

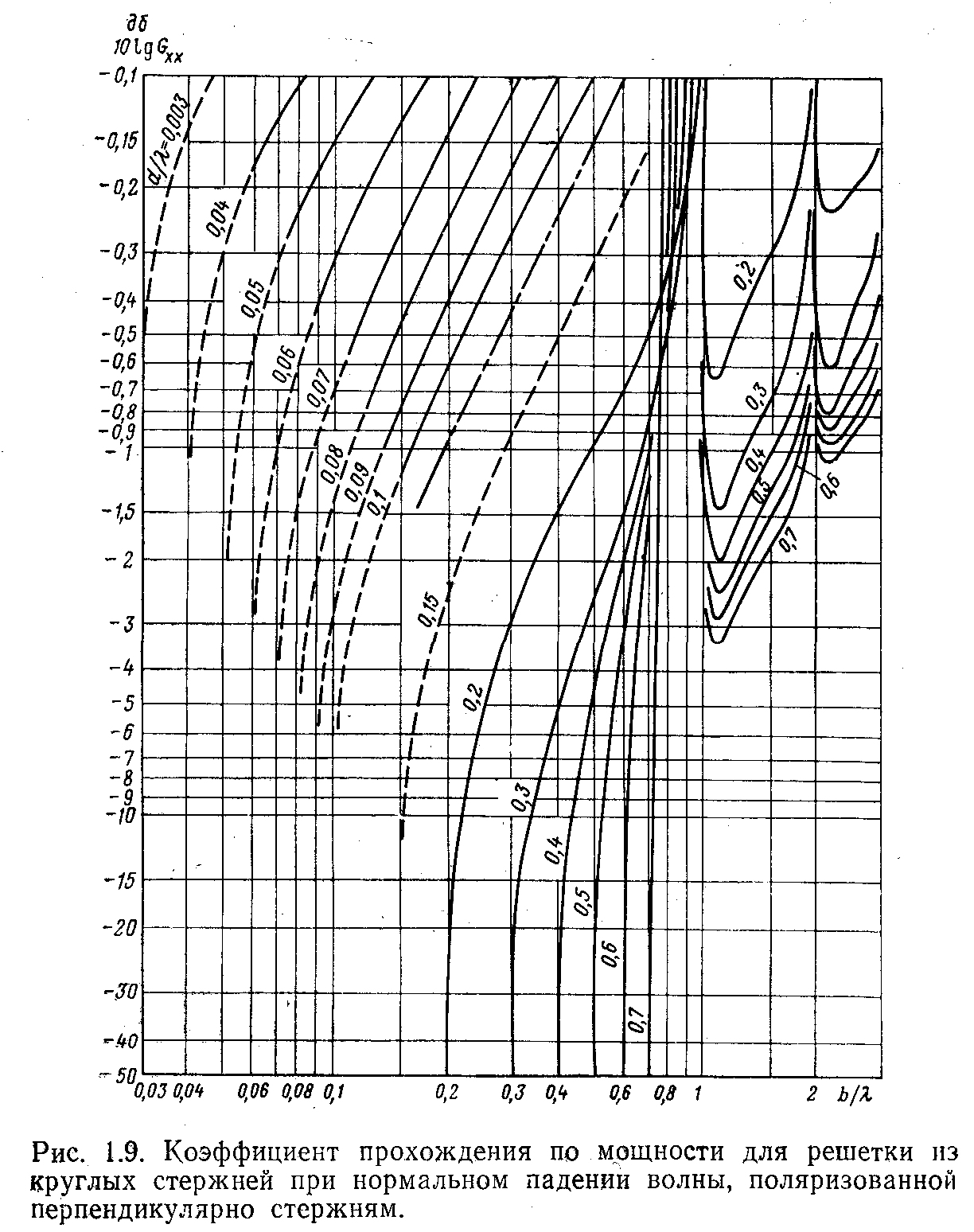
Точность этих формул и предыдущих совпадает. На рис. 1.9 представлена зависимость коэффициента прохождения по мощности от шага решетки и диаметра стержней.

Рис. 1.9 показывает, что решетка из емкостных стержней пропускает более 95% мощности при шаге если . Когда шаг решетки приближается к длине волны то коэффициент пропускания стремится к единице . Если же шаг решетки уменьшается, то, как и в предыдущем случае,

.

При падении на решетку волны, поляризованной под углом к оси Y коэффициенты отражения и прохождения при параллельном приеме равны

(2)

.

36