2.6. Дифференцирование неявных и параметрически заданных функций.

1. Неявные функции.

Если у как функция от х задается посредством соотношения

F (x, y) = 0, (1)

где F (x, y) – выражение, содержащее х и у, то у называется неявной функцией от х. В некоторых случаях уравнение (1) удается разрешить относительно у, и тогда можно перейти от неявного способа задания функции к явному у = f (x), в других случаях такой переход оказывается неосуществимым. Независимо от возможности такого перехода производная от у по х при неявном способе задания функции может быть определена следующим образом: 1. Находим производную от левой части равенства (1), рассматривая при этом у как функцию от х, и приравниваем ее нулю. 2. Решаем полученное уравнение относительно у^/; в результате будем иметь выражение производной от неявной функции в виде

у^/ = f (x). (2)

для определения второй производной от неявной функции дифференцируем равенство (2) (снова рассматривая у как функцию от х), а затем в правой части заменяем у^/ его выражением из равенства (2). Аналогично поступаем при определении производных более высоких порядков.

Примеры решения задач.

40. Дана неявная функция х³ у² + 5ху + 4 = 0. Найти у^/.

Дифференцируем заданное соотношение, рассматривая у как функцию от х:

3х² у² +2х³уу^/ +5у + 5ху^/ = 0.

Решаем полученное уравнение относительно у^/:

41. Дана неявная функция arctg y – y + x = 0. Найти у^//.

Дифференцируем заданное соотношение и определяем затем у^/:

, или у^/ – у^/ – у² у^/ + 1 + у² = 0, откуда Далее находим у^//: у^// = – 2у^–3 у^/ = . Теперь в правую часть полученного равенства подставляем вместо у^/ его значение, полученное ранее:

42. Дан эллипс . Найти уравнение касательной, проходящей через точку М (х₁; у₁), лежащую на эллипсе. Приписываем уравнение эллипса в виде:

а² у² + b² х²= а² b². (*)

Т. к. точка М (х₁; у₁) лежит на эллипсе, то имеет место тождество:

а² у²₁ + b² х²₁ = а² b². (**)

Дифференцируем обе части равенства (*) и находим у^/:

Находим значение производной у^/ в точке М (х₁; у₁). Это значение равно угловому коэффициенту к касательной к эллипсу, проходящей через точку М (х₁; у₁): .

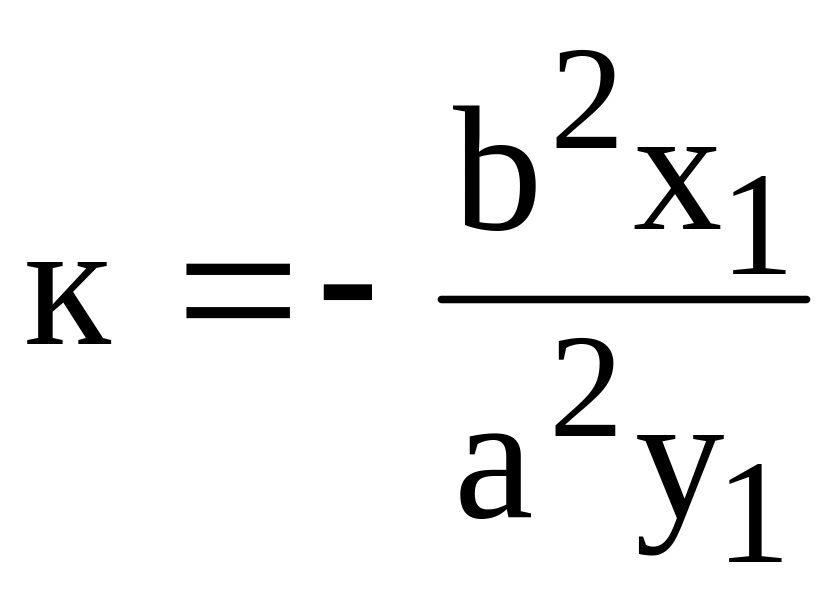Уравнение касательной, проходящей через точку М (х₁; у₁), запишется в виде 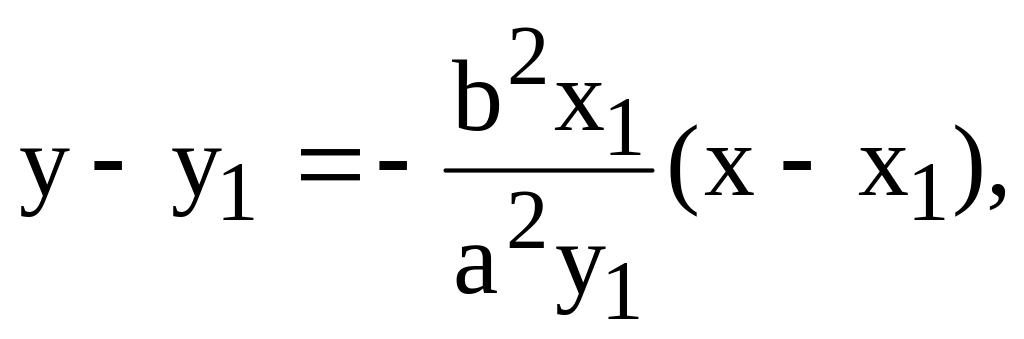или после преобразований а² у₁ у + b² х₁ х = а² у²₁ + b² х²₁.

Учитывая (**), имеем b² х₁ х + а² у₁ у = а² b².

Поделив обе части последнего уравнения на а² b², получаем окончательно:

2. Функции, заданные параметрически.

Пусть функция у аргумента х задается при помощи параметрических соотношений

х = α (t), y = β (t), (3)

причем α (t) и β (t) – дифференцируемые функции t и α^/ (t) ≠ 0. Производная от у по х находится путем дифференцирования равенств (3):

dx = α^/ (t) dt, dy = β^/ (t) dt, (4)

откуда

(5)

Вторую производную от у по х находим, дифференцируя по х соотношение (5):

Примеры решения задач.

43. Дана функция Найти .

Дифференцируем исходные равенства:

dx = – 3 a cos² t sin t dt; dy = 3 a sin² t cos t dt, откуда .

Находим вторую производную:

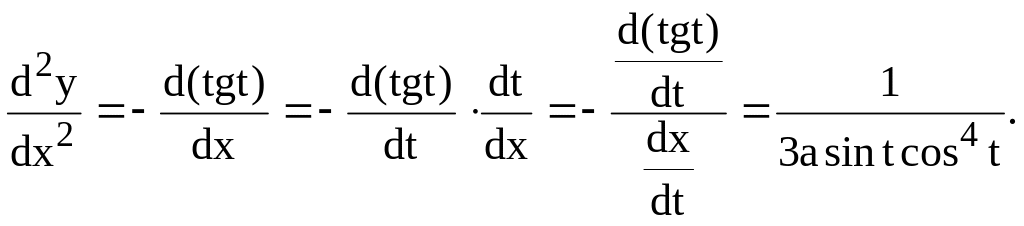
44. Дана функция . Найти у^//.

Дифференцируем исходные соотношения: откуда

Находим вторую производную:

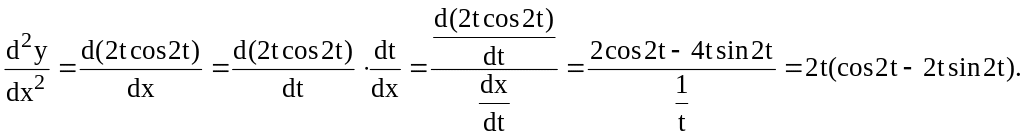
Задачи для самостоятельного решения.

(1 - 101) Найти производные функции.

1. .	2. .
3. .	4. .
5. .	6. .
7. .	8. .
9. .	10. .
11. .	12. .
13. .	14. .
15. .	16. .
17. .	18. .
19. .	20. .
21. .	22. .
23. .	24. .
25. .	26. .
27. .	28. .
29. .	30. .
31. .	32. .
33. .	34. .
35. .	36. .
37. .	38. .
39. .	40. .
41. .	42. .
43. .	44. .
45. .	46. .
47. .	48. .
49. .	50. .
51. .	52. .
53. .	54. .
55. .	56. .
57. .	58. .
59. .	60. .
61. .	62. .
63. .	64. .
65. .	66. .
67. .	68. .
69. .	70. .
71. .	72. .
73. .	74. .
75. .	76. .
77. .	78. .
79. .	80. .
81. .	82. .
83. .	84. .
85. .	86. .
87. .	88. .
89. .	90. .
91. .	92. .
93. .	94. .
95. .	96.
97.	98.
99.	100.
101.

(102 - 116) Вычислить указанных производных для следующих функций:

102. .	103. .
104. .
105. .
106. .
107. .
108. .
109. .
110. .
111. .
112. .	113. .
114. .	115. .

(116 – 120) Решить уравнение , если:

116. .	117. .
118. .	119. .
120. .

(121–123) Найти , если:

121. . 122. .

123. .

(124–131) Найти для функций , заданных параметрически:

124. .

125. .

126. .

127. .

128. .

129. .

130. .

131. .

(132 – 134) Найти для функций , заданных параметрически:

132. .

133. .

134. .

(135 – 143) Найти для дифференцируемых функций заданных неявно следующими уравнениями:

135. .	136. .
137. .	138. .
139. .	140. .
141. .	142. .
143. .

(144 – 147) Для дифференцируемых функций , заданных неявно, вычислить :

144 .

145. .

146. .

147. .

(148 – 156) Найти дифференциалы:

148. .	149. .
150. .	151. .
152. .	153. .
154. .	155. .
156. .

(157 – 160) Найти дифференциалы в указанных точках:

157. .	158. .
159. .	160.

(161 – 170) В указанных точках найти дифференциалы функций у = у(х), заданных неявными или параметрическими уравнениями:

161. (1; 2).	162. .
163. .	164. .
165. .	166. .
167. .	168. .
169. .	170. .

171. В точке (0;а) найти дифференциал функции у = у(х), заданной в полярной системе координат уравнением .

(177 - 178) Найти дифференциал функции у, считая известными дифференциалы функций u и v:

172. v.	173. v.
174. v/ .	175. .
176. .	177. .

(178 – 185) Заменяя приращение функции дифференциалом, найти приближенное значение функции

у = у(х) в указанных точках:

178. , а) , б) .

179. , а) , б) .

180. , а) , б) .

181. , а) .

182. , .

183. , .

184. , .

185. , .

(186 – 195)Найти углы, под которыми график функции у = f(х), пересекать ось абсцисс:

186. .	187. .
188. .	189. .
190. .	191. .
192. .	193. .
194. .	195. .

(196 –204) Найти точки, в которых касательные к графику функции у = f(х) параллельны оси абсцисс:

196. .	197. .
198. .	199. .
200. .	201. .
202. .	203. .
204. .

(205 – 213) Написать уравнение к касательной к графику функции у = f(х) в указанной точке:

205. .	206. .
207. .	208. .
209. .	210. .
211. .	212. .
213. .

214. Написать уравнение касательной к эллипсу в точке (х₀,у₀).

215. Найти точки пересечения касательных к эллипсам в точках с абсциссой х₀ с осью абсцисс.

216. Найти угол между касательными к кривой , проходящими через точку (3; 4).

(217 – 222) Написать уравнение к нормали к графику функции у = f(х) в указанной точке:

217. .	218. .
219. .	220. .
221. .	222. .

223. Написать уравнение нормали к эллипсу , в точке (-2; 1).

224. Написать уравнение к гиперболе в точке (х₀;у₀).

(225 – 235) Написать уравнение касательной и нормали к кривой в точке M:

225. .
226.
227.	228.
229.	230. .
231.	232.
233.	234.
235.

(236 – 244) Определить, в каких точках и под каким углом пересекаются графики функций:

236. .	237. .
238. .	239. .
240. .	241. .
242. .	243. .
244. , - всюду дифференцируемая функция.

(245 – 252) Определить, в каких точках и под каким углом пересекаются кривые:

245. и .	246. и .
247. и .	248. и .
249. и .	250. и .
251 и .	252. и .

(253 – 262) Найти производную второго порядка.

253. .	254. .
255. .	256. .
257. .	258. .
259. .	260. .
261. .	262. .

(263 – 266) Найти вторую производную в указанной точке:

263. .	264. .
265. .	266. .

(267 – 270) Найти второй дифференциал функции:

267.	268.
269.	270.

(271 – 274) Найти для функций, заданных параметрически уравнениями:

271. .	272. .
273. .	274. .
275. .

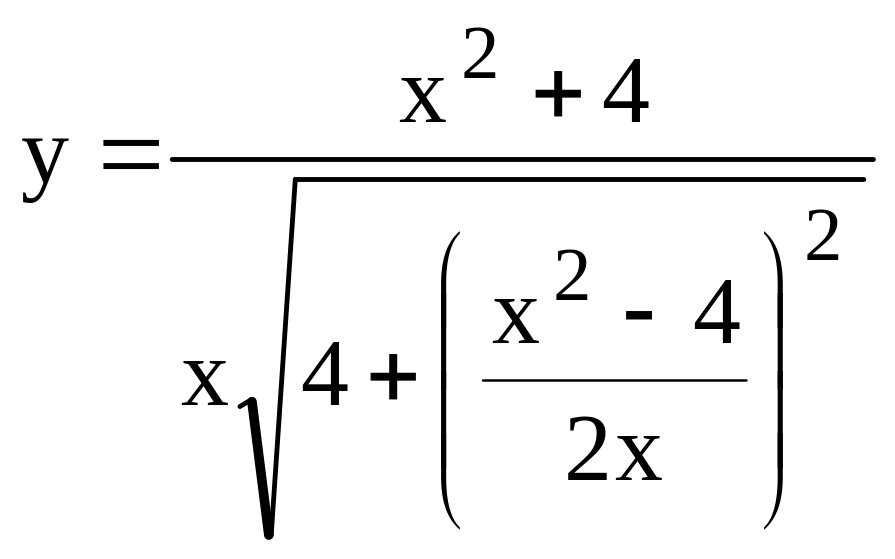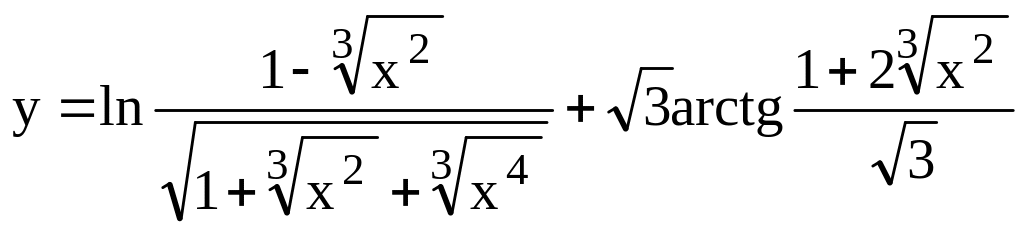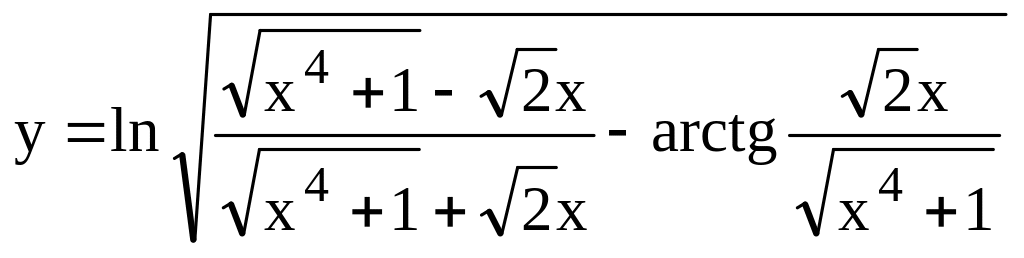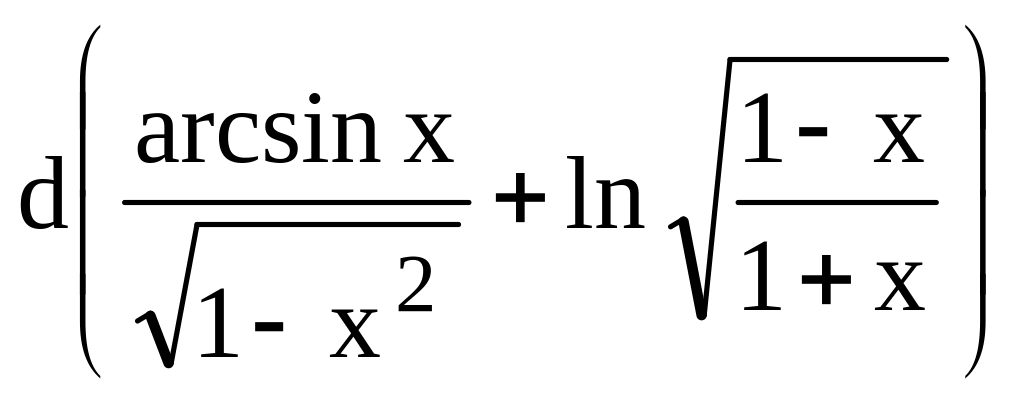66