Основные правила нахождения дифференциалов.

(аналогичны основным правилам вычисления производных)

d (c) = 0 (15) d (uv) = u dv + v du (18)

d (u ± v) = du ± dv (16) (19)

d (cu) = cdu (17)

(здесь с – постоянная, а u и v – функции от х, имеющие производные).

Положим теперь, что задается функция от функции у = f (u), где u – функция аргумента х. По правилу дифференцирования функции от функции и по определению дифференциала, dy = f^/ (u) u^/ dx.

Но u^/ = du / dx, поэтому dy = f^/ (u) u^/ du / dx или dy = f^/ (u) u^/ du. (20)

Заметим, что формула (20), по которой находится дифференциал функции f (u), имеет совершенно такой же вид, как и формула (1), по которой определяется дифференциал функции f (x). Это свойство дифференциала сохранять неизменной свою форму независимо от того, задается ли функция f (x) аргумента х или функция от функции f (u), называется свойством инвариантности.

Производная (в отличие от дифференциала) не обладает свойством инвариантности. Действительно, если y = f (x), то y^/ = f^/ (x), а если y = f (u), то y^/ = f^/ (u) u^/.

Учитывая свойство инвариантности дифференциала, можно составить таблицу дифференциалов сложных функций:

d (u^α) = α u^α–1du (21)

(α – любое действительное число)

(22) (29)

d (ln u)= (23) (30)

d (a^u) = a^u ln a du (24) d (arccos u) (31)

d (e^u) = e^u du (25) (32)

d (sin u) = cos u du (26) (33)

d (cos u) = – sin u du (27)

(28)

В последующих примерах требуется найти дифференциалы от заданных функций.

Примеры решения задач.

31. у = (1 + tg x)⁸. Решим задачу 2- мя способами.

Первый способ.

Находим производную от заданной функции: у^/ = 8(1 + tg x)⁷ , откуда по определению дифференциала dу = 8(1 + tg x)⁷ .

Второй способ.

Дифференциал находим непосредственно, используя формулы (21) и (28):

dу = 8(1 + tg x)⁷d (1 + tg x) = 8 (1 + tg x)⁷ .

32. у = ln arctg (sin x).

Применяя последовательно формулы (23), (32) и (26), вычисляем дифференциал непосредственно:

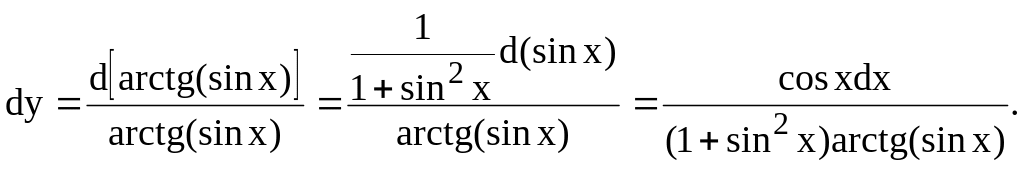
При некотором навыке запись может быть сокращена и окончательный ответ получается сразу.

2. Применение дифференциала к приближенным вычислениям.

Дифференциал dy функции y = f (x) представляет собой главную часть приращения этой функции, линейную относительно ∆х. Иными словами, приращение ∆у связано с дифференциалом соотношением

Таким образом, разность между приращением и дифференциалом функции есть бесконечно малая высшего порядка, поэтому при f^/ (x) ≠ 0 , т. е. приращение функции и ее дифференциал – эквивалентны бесконечно малые. Отсюда следует, что при малых ∆х имеет место приближенное равенство

∆у ≈ dy, или f (x + ∆x) – f (x) ≈ f^/(x) ∆x. (34)

Соотношение (34) часто используется в приближенных вычислениях.

Примеры решения задач.

33. Вывести приближенную формулу (35)

при условии, что мало по сравнению с х.

В данном случае f (x) = , поэтому f (x + ∆x) = . Подставляя полученные выражения в формулу (34), получим искомую приближенную формулу.

34. Показать, что при малом α.

Полагаем в формуле (35) х = 1 и заменяем х = на α. В результате получаем искомое выражение.