Тема № 2. Производная и дифференциал.

2.1. Производные простых функций.

1. Определение производной.

Производной функции у = f (x) по аргументу х называется предел отношения приращения функции к приращению независимого переменного (аргумента) при условии что это последнее стремится к нулю.

Производная функции у = f (x) обозначается через у^/ или f^/ (x). Таким образом, по определению

Операция отыскания производной f^/ (x) данной функции f (x) называется дифференцированием этой функции.

2. Табличные производные.

(1) (8)

(α – любое действительное число) (9)

(2) (10)

(3) (11)

(4) (12)

(5) (13)

(6) (3а)

(7)

Следует отметить, что формула (2) является частным случаем формулы (1) при α = ½. Точно так же формула (5) получается как частный случай формулы (4) при а = е.

3. Основные правила дифференцирования.

(с)^/ = 0 (14) (uv)^/ = uv^/ + u^/v (17)

(u + v)^/ = u^/ + v^/ (15) (18)

(cu)^/ = cu^/ (16)

(здесь с – постоянная, а u и v – функции от х, имеющие производные).

Примеры решения задач.

1. Найти производную от функции у = 5х³ – 2х² + 3х – 4.

Основываясь на формулу (15), имеем: у^/ = (5х³)^/ – (2х²)^/ + (3х)^/ – (4)^/. Далее, применяя формулы (16) и (17), получаем: у^/ = 5(х³)^/ –2 (х²)^/ + 3(х)^/. Наконец, пользуясь формулой (1), приходим к окончательному результату: у^/ = 5· 3х² – 2·2х + 3·1 = 15х² – 4х + + 3.

Разумеется, при минимальном навыке промежуточные выкладки сокращаются (или опускаются вовсе).

2. Найти у^/, если у = х⁴ – 6х² + 8. у^/ = 4х³ – 12х.

3. Найти у^/, если .

Переписываем данное выражение, используя дробные и отрицательные показатели: .

И тогда, применяя те же формулы, что в задании 1, получим:

или после очевидных преобразований

4. Дано у = х³ · cos x. Найти у^/.

По правилам дифференцирования произведения получаем: у^/ = х³ (– sin х) + 3x² cos x = – x³ sin x + 3x² cosx.

(понятно, что здесь применялись также формулы (1) и (7)).

5. Найти у^/, если .

Применяя правило дифференцирования дроби, а также формулы (1) и (12), находим: .

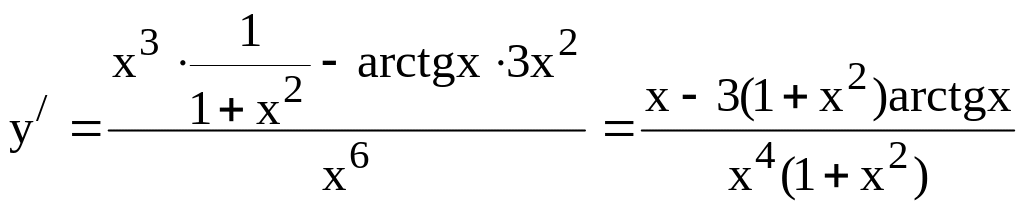2.2. Производные сложных функций.

1. Теорема о дифференцировании сложной функции.

Приведенные выше правила и формулы дифференцирования позволяют находить производные от функций только в самых простых случаях. Знания этих правил и формул недостаточно для дифференцирования функций более сложного вида, например, таких, как , у = е^arctgx и т. д.

В подобных случаях пользуются более общими формулами дифференцирования, основанными на теореме о производной функции от функции.

Пусть у = f [φ (x)] – сложная функция, т. е. у = f (u), а u = φ (x). Если для соответствующих друг другу значений х и u существуют производные f^/ (u) и u^/ = φ^/ (x), то существует и производная от у по х, причем у^/ = f^/ (u) · u^/_х.

Пользуясь этим соотношением, можно получить таблицу дифференцирования:

(1) (8)

(α – любое действительное число) (9)

(2) (10)

(3) (11)

(4) (12)

(5) (13)

(6) (7)

Понятно, что формула (2) есть частный случай формулы (1), а формула (5) – частный случай формулы (4).

Примеры решения задач.

6. Найти производную от функции .

Вводим вспомогательную функцию u, полагая u = х² +3х +1. Тогда, очевидно, можно записать , где u = х² +3х +1.

По формуле (2) имеем , или окончательно, заменяя u его значением: .

7. Найти у^/, если у = (х² + 5х + 7)⁸.

Полагая u = х² + 5х + 7, имеем у = u⁸. По формуле (1) у^/ = 8u⁷ (2х+5) или окончательно у^/ = 8 (х² + 5х + 7)⁷ (2х + 5).

Следует заметить, что к такой подробной записи прибегают только в самой начальной стадии освоения техники дифференцирования: обычно же вспомогательная функция вводится мысленно, что и рекомендуется делать в дальнейшем.

8. Найти у^/, если у =ln (х³ + 7х + 2).

Принимая в данном случае за u (мысленно) выражение х³ + 7х + 2 и пользуясь формулой (3), получим:

.

9. Найти у^/, если у =ln (arctg x).

В данном случае роль u будет играть arctg x. Применение формулы (3) дает:

.

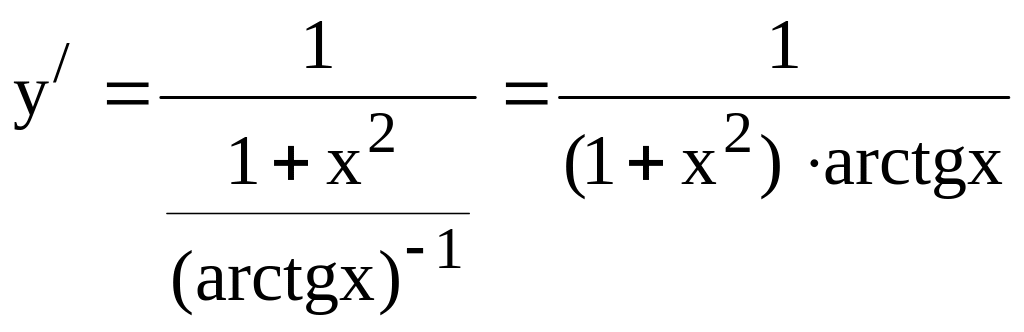10. Найти производную от функции у = е^{arcsin x}.

Принимая arcsin x за u и применяя формулу (5), имеем: .

11. Найти у^/, если у = sin³x. Следует напомнить, что обозначением sin³x пользуются только для краткости записи и что sin³x = (sin x)³.

Таким образом, фактически имеем дело с дифференцированием функции у = (sin x)³. Принимая sin x за u и пользуясь формулой (1), получаем:

у^/ = 3 (sin x)²· cos x = 3 sin² x cos x.

12. Найти у^/, если у = arcsinx.

По правилу дифференцирования произведения получаем сначала у^/ = (arcsinx)^/ + arcsinx ( )^/.

При вычислении производной от принимаем 1 – х² за u. И тогда по формуле (2):

.

Таким образом,