2.5. Сбор фактического материала

После того, как обозначен предмет исследования, определен объект изучения, можно приступать к сбору фактов. Однако это возможно лишь при наличии соответствующих методов или конкретной методики. Выбор методов или конкретной методики обусловлен теми целями и задачами, которые стоят перед исследователем. Требование здесь простое: методы получения фактов должны быть адекватны предмету исследования и по возможности не оказывать влияния на объект.

Студенты в своих исследованиях обычно используют методы наблюдения, беседы, анализа продуктов деятельности, эксперимент. Важно, чтобы факты были достоверными и в достаточном количестве. Для успешного сбора фактического материала необходимо спланировать эту работу и протоколировать ее ход и результаты.

2.6. Статистическая обработка фактического материала

Любая наука в той или иной степени использует математику. Существует даже мнение, что наука лишь в той мере является наукой, в какой она пользуется математикой. В научном же исследовании без математики невозможно обойтись. Она помогает упорядочить фактический материал, сделать его более удобным для восприятия и последующего анализа; наконец, без математической обработки невозможно с уверенностью утверждать, что выводы, полученные в исследовании, достоверны.

В этом разделе показаны основные приемы упорядочивания и статистической обработки результатов проведенного исследования.

2.6.1. Методы статистической обработки информации

Методами статистической обработки результатов исследования называются математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе исследования, можно обобщать, приводить в систему, выявляя скрытые в них закономерности [7; с. 22].

Все методы математико-статистического анализа условно делятся на первичные и вторичные.

Первичными называются методы, с помощью которых можно получить показатели, непосредственно отражающие результаты проводимых в эксперименте измерений. Соответственно под первичными статистическими показателями имеются в виду те, которые применяются в самих психодиагностических методиках и являются итогом начальной статистической обработки результатов исследования.

Вторичными называются методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности. Вторичные методы позволяют оценивать степень случайности того или иного явления, той или иной взаимосвязи явлений. Вторичные методы непосредственно проверяют, доказывают или опровергают гипотезы, поставленные в ходе исследования.

Показатели исследования – измеряемые признаки внешних действий испытуемых, их высказываний и скрытых физиологических реакций.

Варианты – числа представляющие собой результаты измерений (единичные показатели).

Вариационный ряд – все замеры, расположенные в один ряд в порядке возрастания или убывания.

Медианой называется значение изучаемого признака, который делит выборку, упорядоченную по величине данного признака пополам.

Модой называют количественное значение исследуемого признака, наиболее часто встречающееся в выборке.

Интервалом называется группа, упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением [9; С. 120-122].

Среднеарифметическое значение представляет собой среднюю оценку, изучаемого в эксперименте психологического качества вычисляется во всех случаях, когда произведено интегральное измерение, и находится путем суммирования всех результатов и делением получившейся суммы на число членов вариационного ряда

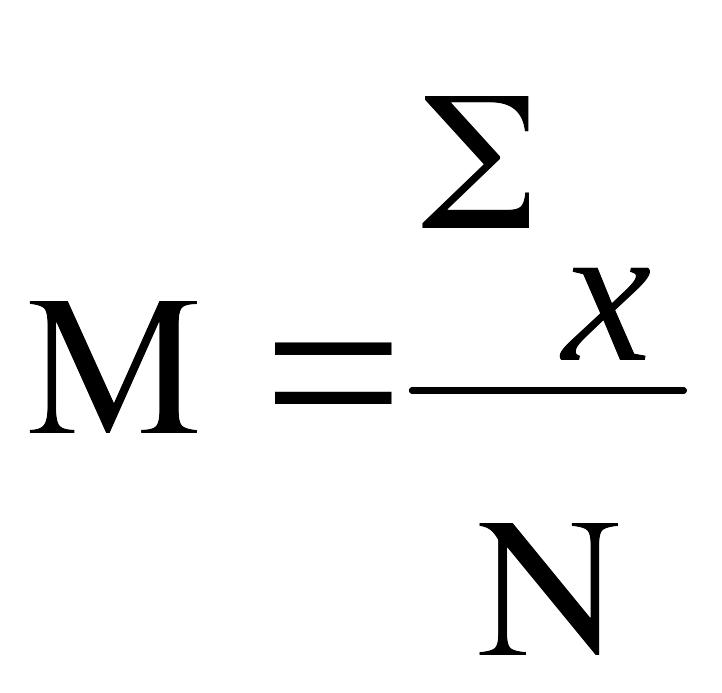, где М – средняя арифметическая;  - знак суммирования

Если произведено N измерений, то полученные единичные показатели обозначаются как Х₁, Х₂, Х₃………Х_n

Для измерения вариации оценок внутри группы пользуются другими характеристиками вариационного ряда – дисперсией и средним квадратическим отклонением [7; С. 23].

Дисперсия, как статистическая величина характеризует насколько частые значения отклоняются от средней величины в одной выборке. Определяется дисперсия как средний как средний квадрат отклонения варианты от ее среднего арифметического значения и обозначается буквой ₂.

Для вычисления дисперсии, от каждой из вариант Х, вычитают значение средней арифметической М. Получают ряд величин отклонений:

d = X – M

Теперь нужно найти среднее отклонение от средней арифметической М. По сумме всех отклонений d равна нулю, т.к. одни отклонения от М положительны, а другие отрицательны. Поэтому суммируют не отклонения d, а их квадраты. Полученную сумму делят на число вариант N, в результате чего получают величину ², которая называется дисперсией.

d² =

Квадратный корень из дисперсии и есть интересующее нас среднее отклонение от М:

d =

Эта величина  (сигма) называется средним квадратическим отклонением. Теперь зная величины М и , мы имеем полную статистическую характеристику совокупности вариант Х₁, Х₂, Х₃………Х_n

Значение М и  достаточно и для сравнения между собой двух средних арифметических. Мы можем определить имеется ли между М₁ и М₂ существенное (статистически значимое) различие или нет.

Для определения статистической достоверности разницы М₁ и М₂ пользуются критерием Стьюдента t.

t = ,

где m₁ m₂ представляют собой величины средних ошибок, которые вычисляются по формуле:

Величина t дает возможность определить не только достоверность различия средних М₁ и М₂, но и определить уровень достоверности. Для этого существуют специальные таблицы определения уровня значимости.

Таблица 1

Числостепенейсвободы	Уровни значимости, p
	0,05	0,01	0,001
5	2,57	4,03	6,87
10	2,23	3,17	4,59
20	2,09	2,84	3,85
30	2,04	2,75	3,65
60	2,00	2,66	3,46
	1,96	2,58	3,29

В таблице представлены величины t для трех уровней достоверности: пятипроцентного (Р = 0,05), однопроцентного (Р = 0,01), однопромилльного

(Р = 0,001)

Критерий Стьюдента - t дает нам возможность поэлементного анализа сложноорганизованных объектов действительности. Исходя из результатов исследований в школе В.В.Белоуса, поэлементная и интегральная характеристики не совпадают. Для интегрального анализа нам необходимо вычислить линейный дискриминатор. Его суть заключается в следующем. Если между попарно взятыми показателями разных объектов отсутствует линейная корреляция, то ее можно обнаружить не частным, а комплексным способом, т.е. путем сопоставления системы показателей друг с другом. С математической точки зрения такой интегральный показатель может быть установлен на основе дискриминантного анализа. С этой целью широко используется формула, предложенная О.М.Калининым:

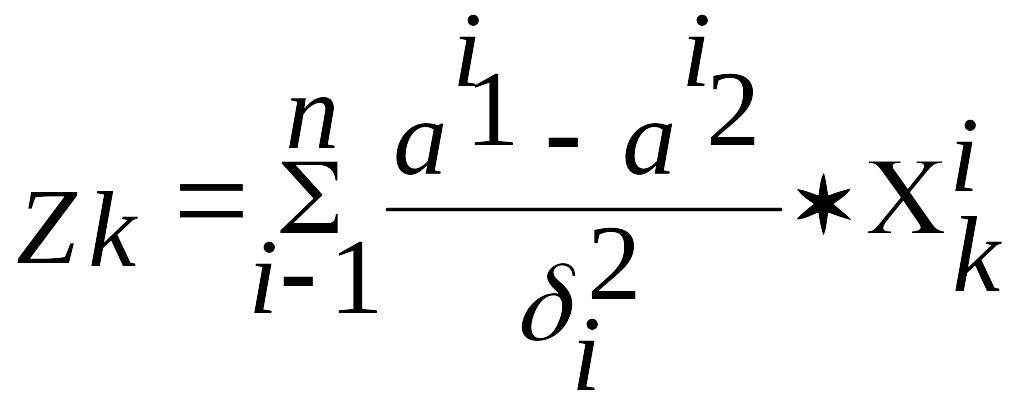, где

а₁ - среднеарифметическое (i-того) отдельного показателя 1-ой группы;

а₂ - среднеарифметическое (i-того) отдельного показателя 2-ой группы;

_i - среднеквадратическое отклонение по совокупности i-ых показателей в 1 и 2 группах;

- абсолютное выражение каждого испытуемого по каждому показателю;

i - 1,2,3,…n (n- число показателей);

k - номер испытуемого;

 - суммирование по всем нормированным показателям.

Статистическое сравнение по комплексным показателям тоже осуществляется с помощью t-критерия Стьюдента (квантили t-распределения Стьюдента смотри в приложении 1).

Говоря о преимуществах линейного дискриминатора по сравнению с поэлементным сравнением, мы, тем не менее, должны признать, что линейная дискриминантная функция не в состоянии дать конкретное и детализированное представление о характере зависимостей свойств рассматриваемой психической реальности. Такого рода информация может быть получена из результатов корреляционного анализа [5].

Чтобы исследовать меру статистической взаимосвязи между показателями вычисляется коэффициент корреляции (критические значения выборочного коэффициента линейной корреляции

Корреляционный анализ

Для практического психолога или психодиагноста очень важно владеть оперативными статистическими методами обработки экспериментальных данных, не требующими машинной обработки. К таким практическим методам относится ранговый коэффициент корреляции, который поможет психологам и педагогам определить статистическую связь, зависимость между экспериментальными и "жизненными" показателями, подтвердить прогностическую силу данного теста.

Определение взаимосвязи показателей, измененных в шкале порядка, производят с использованием ранговых коэффициентов корреляции.

Мы познакомимся с одним из них - ранговым коэффициентом корреляции Спирмена (обозначается буквой r). Его вычисляют по формуле:

, где:

d = x₁ - y₁ - разность рангов данной пары показателей;

х - место, занятое в математической олимпиаде;

у - число месяцев занятий в математической школе конкретного ученика.

Все прочие условия (класс, возраст, пол и др.) примерно одинаковы. Результаты наблюдений и опроса представлены в таблице 2 (столбцы 1 и 2).

Так как показатели изменены в шкале порядка, вычислим значение рангового коэффициента корреляции.

Запишем алгоритм вычисления рангового коэффициента корреляции Спирмена (r) по шагам.

Шаг 1. Проранжировать (упорядочить и приписать порядковые номера) показатели х и у. Так как х уже упорядочен и обозначает соответствующие ранги, перепишем его значения в столбец 3. Показателю у приписываем ранги следующим образом: значению 10 – ранг 1; 9 – ранг (2+3)/2= 2,5; 8-ранг 4 и т.д.

Таблица 2

Расчет рангового коэффициента корреляции Спирмена

№ пп	1	2	3	4	5	6
	X	У	X1	Y1	X1-Y1	(X1-Y1)2
1.	1	9	1	2,5	-1,5	2,25
2.	2	10	2	1	1	1
3.	3	8	3	4	-1	1
4.	4	7	4	5	-1	1
5.	5	9	5	2,5	2,5	6,25
6.	6	4	6	75	-1,5	2,25
7.	7	4	7	7,5	-0,5	0,25
8.	8	3	8	95	1.5	2,25
9.	9	5	9	6	3	9
10.	10	3	10	9,5	0,5	0,25
Сумма  = 25,5

Шаг 2. Вычислить разность рангов d = (xl-yl) (столбец 5);

Шаг 3. Вычислить квадрат разности d2= (x_l-y_l)² (столбец 6);

Шаг 4. Вычислить сумму квадратов разности d² = 25,5 Шаг 5. Вычислите значение r

Значение r = 0,846 характеризует сильную положительную взаимосвязь. Другими словами, опыт, накопленный в математической школе, достаточно сильно определяет успешность выступления на математической олимпиаде при прочих равных условиях.

Ранговый коэффициент корреляции Спирмена изменяется в пределах от -1 до +1. Достоинством ранговых коэффициентов корреляции является простота вычисления. Поэтому ими следует пользоваться для быстрой оценки взаимосвязи, когда показатели или признаки не могут быть изменены точно, но могут быть ранжированы.

В таблице 3 представлены критические значения коэффициентов корреляции для различных степеней свободы. Заметим, что зависимость коэффициента корреляции зависит и от заданного уровня значимости или принятой вероятности допустимой ошибки в расчетах.

Таблица 3

Критические значения коэффициентов корреляции для различных степеней свободы

Числостепенейсвободы	Коэффициент корреляции
	0,1	0,05	0,01
2	0,900	0,950	0,990
3	0,805	0,848	0,959
4	0,729	0,811	0,917
5	0,669	0,754	0,874
6	0,622	0,707	0,834
7	0,582	0,666	0,798
8	0,549	0,632	0,765
9	0,521	0,602-	0,735
10	0,497	0,576	0,708
20	0,360	0,423	0,537
30	0,296	0,349	0,449
50	0,239	0,272	0,354

Метод множественных корреляций в отличие от метода парных корреляций позволяет выявить общую структуру корреляционных зависимостей, существующих внутри многомерного экспериментального материала, включающегося более двух переменных, и представить эти корреляционные зависимости в виде некоторой системы.

Анализ взаимосвязи между большим количеством переменных осуществляется путем использования многомерных методов статистической обработки вручную или с применением ЭВМ. Цель применения подобных методов – сделать наглядным скрытые закономерности, выделить наиболее существенные взаимосвязи между переменными. Примерами таких многомерных статистических методов являются:

1. многомерное шкалирование;

1. факторный анализ;

2. кластерный анализ (кластер – гроздь);

3. латентно-структурный анализ.

Многомерное шкалирование обеспечивает наглядную оценку сходства и различия между некоторыми объектами, описываемыми большим количеством разнообразных переменных. Эти различия представляются в виде расстояния между оцениваемыми объектами в многомерном пространстве [5; С. 32].

Факторный анализ заключается в выявлении и интерпретации факторов. Фактор – обобщенная переменная, которая позволяет свернуть часть информации, т.е. представить ее в удобообозримом виде. Например, факторная теория личности выделяет ряд обобщенных характеристик поведения, которые в данном случае называются чертами личности.

Факторный анализ не является однородной процедурой, а распадается на ряд «техник» (рисунок 1). R-техника – это традиционный факторный анализ матрицы интеркорреляций показателей различных тестов. Осуществление Q-техники факторного анализа требует вычисления матрицы интеркорреляций показателей разных испытуемых по различным тестам. Это может быть осуществлено при проведении не только нормативного, но и ипсативного измерения. Q- и R-техники различаются по виду выделяемых факторов. R-техники дают факторы, отражающие структуру тестов, а Q-техники – факторы сходства и различия испытуемых.

R-техника состоит в факторном анализе матрицы интеркорреляции значений показателей обследуемых по одним и тем же тестам, но в различные промежутки времени. Эта техника позволяет выявить факторы, обусловливающие изменение величин показателей тестов. Кроме этого, для анализа факторов измерений (состояний) используется так называемая dR-техника факторного анализа, в которой исходным материалом являются матрицы интеркорреляций изменений (разностей) показателей тестов между двумя моментами времени

Кластерный анализ позволяет выделить ведущий признак и иерархию взаимосвязей признаков.

Латентно-структурный анализ представляет совокупность аналитико-статистических процедур выявления скрытых переменных (признаков), а также внутренней структуры связей между этими признаками. Он дает возможность исследования проявления сложных взаимосвязей непосредственно ненаблюдаемых характеристик социально-психологических явлений. Латентный анализ может являться основой для моделирования указанных взаимосвязей.

2.7. Интерпретация экспериментальных данных [ 10 с.132-134]

Обычно интерпретация понимается как совокупность значений (смыслов), придаваемых определенным способом различным данным (в более общем смысле: теориям, символам, формулам, выражениям и т.п.). Другими словами, интерпретировать что-то – значит, приписать (присвоить) этому содержательный смысл.

Роль и значение интерпретации велики. Правильная интерпретация позволяет сопоставлять научные концепции с описываемыми ими фрагментами реального мира, порождать практические рекомендации, предлагать оптимальные способы действия и т.п. Обычно интерпретация основывается на исходных данных.