
- •Кафедра «Сельскохозяйственные машины» п. Е. Родзевич, Кирилюк с.И., Миренков в.В.
- •Практикум
- •Содержание
- •Лабораторная работа № 1 Определение механических характеристик материалов при растяжении-сжатии
- •Теоретическая часть
- •Постановка опыта
- •2.1. Испытание стали при растяжении
- •2.2. Испытание материалов при сжатии
- •3. Техника безопасности
- •4. Обработка результатов измерений
- •Механические характеристики и характеристики пластичности материалов
- •Эскизы образцов до и после опытов
- •5. Оформление отчета
- •Контрольные вопросы
- •Литература
- •Лабораторная работа № 2 Определение модуля продольной упругости и коэффициента поперечной деформации стали
- •1. Краткие теоретические сведения
- •2. Оборудование
- •Техника безопасности
- •Постановка опыта
- •5. Оформление отчета
- •Контрольные вопросы.
- •Литература
- •Лабораторная работа № 3 Испытание материалов на срез
- •1. Краткие теоретические сведения
- •1.1. Расчет заклепок на срез
- •1.2. Расчет заклепок на смятие
- •1.3. Проверка прочности скрепляемых листов
- •2. Оборудование, приспособление, инструмент
- •3. Техника безопасности
- •4. Постановка опыта
- •5. Обработка результатов опыта
- •6. Оформление отчета
- •1. Краткие теоретические Сведения
- •2. Оборудование
- •3. Техника безопасности
- •4. Постановка опыта
- •4.1. Сравнительное изучение характера разрушения и определение механических характеристик стали и чугуна
- •4.2. Определение модуля сдвига
- •5. Обработка результатов
- •6. Оформление отчета Отчет
- •Результаты сравнительных испытаний материалов
- •Контрольные вопросы
- •Литература
- •Опытная проверка теории изгиба прямого стержня
- •1. Краткие теоретические сведения
- •Метод непосредственного интегрирования дифференциального уравнения изогнутой оси и метод начальных параметров
- •1.2. Определение перемещений с помощью интеграла Мора и способа Верещагина
- •2. Оборудование
- •3. Техника безопасности
- •4. Постановка опыта
- •5. Обработка результатов
- •6. Оформление отчета
- •Контрольные вопросы
- •Литература
- •1. Краткие теоретические сведения
- •2. Оборудование, Приспособление, Инструмент
- •3. Техника безопасности
- •4. Порядок выполнения работы
- •5. Обработка результатов
- •6. Оформление отчета
- •Контрольные вопросы
- •Лабораторная работа № 7 Опытная проверка теории удара
- •1. Краткие тЕоретические сведения
- •2. Оборудование, приспособления, инструмент
- •3. Техника безопасности
- •4. Постановка опыта
- •5. Обработка результатов испытаний
- •6. Оформление отчета
- •Контрольные вопросы
- •Литература
6. Оформление отчета
Отчет
по лабораторной работе “Опытная проверка теория изгиба
прямого стержня”
Цель работы.
Оборудование, приспособление, инструмент.
Схема балки (с указанием размеров, номеров подвесов, индикаторов, тензорезисторов и мест их установки на балке) согласно задания преподавателя.
Постановка опыта с указанием интервала нагрузки:
Таблица 5.1.
Средние арифметические значения прогибов
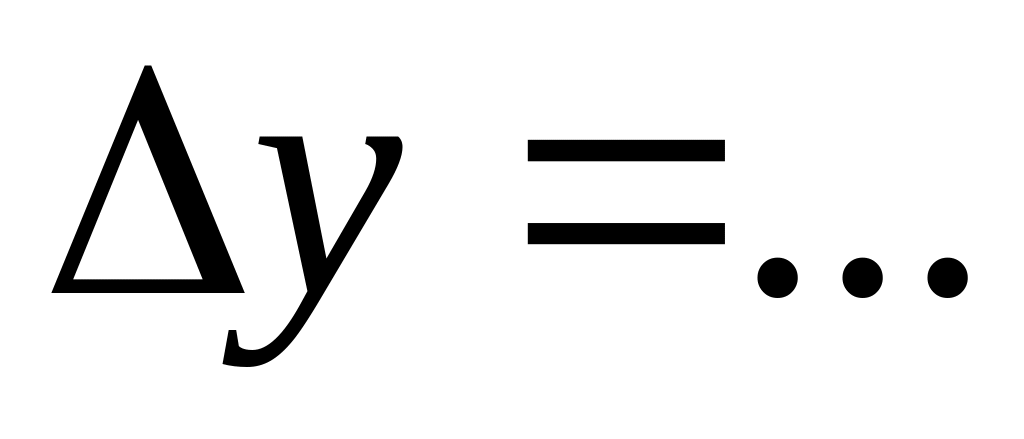 мм.
мм.Среднее арифметическое значение угла поворота
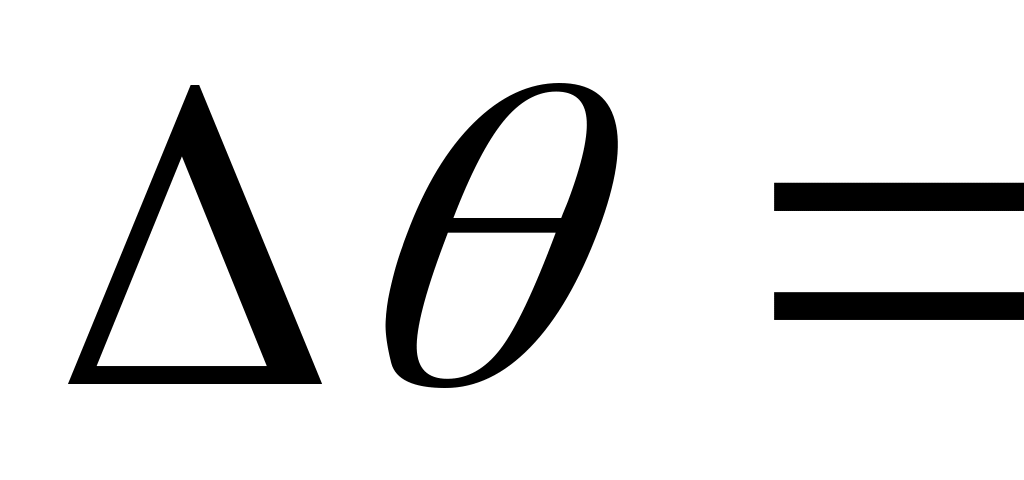 ...
рад (град).
...
рад (град).Теоретическое определение прогибов и углов поворота (метод начальных параметров или способ Верещагина).
Таблица 5.2.
Экспериментальные значения напряжений.
Теоретическое определение напряжений.
Выводы.
Контрольные вопросы
Какие типы опор применяются для закрепления балок к основанию? Покажите опорные реакции, соответствующие каждому виду опор.
Какие уравнения используются для определения значений опорных реакций?
Как проверить правильность определения опорных реакций?
Какие внутренние усилия возникают в поперечных сечениях стержня в общем случае действия на него плоской системы сил?
Что называют плоским (прямым) поперечным изгибом?
Какие правила знаков приняты для каждого из внутренних усилий?
Для приведенных балок записать выражения поперечной силы и изгибающего момента на каждом из участков

Что представляет собой эпюры поперечных сил и изгибающих моментов?
Постройте эпюры поперечных сил и изгибающих моментов для балок, приведение в п.7.
Как формулируется гипотеза плоских сечений?
Что представляет собой нейтральная линия? Как она расположена в балке?
Чему равна кривизна оси балки при чистом изгибе?
Что называется жесткостью сечения при изгибе?
По какой формуле определяются нормальные напряжения в поперечных сечениях балки при поперечном изгибе?
В каких точках балки материал находится в линейном напряженном состоянии?
Запишите закон Гука для линейного напряженного состояния.
Что называется моментом сопротивления сечения при изгибе и какова его размерность?
Какие перемещения получают поперечные сечения балок при изгибе?
Что представляют собой уравнения метода начальных параметров и почему они так называются?
Литература
Феодосьев В.И. Сопротивление материалов. М.: Наука, 1986. – 512 с.
Дарков А.В., Шпиро Г.С. Сопротивление материалов. М.: Высшая школа, 1989. – 624 с.
Афанасьев А.М., Марьин В.А. Лабораторный практикум по сопротивлению материалов. М.: Наука, 1975.
Лабораторная работа № 6
Определение момента защемления однопролетной статически неопределимой балки
Цель работы: сравнение результатов аналитического и экспериментального определения момента защемления однопролетной статически неопределимой балки.
1. Краткие теоретические сведения
Статически неопределимыми называют такие системы, для определения внутренних усилий в которых недостаточно одних уравнений равновесия статики. Другими словами, статически неопределимыми являются такие системы, в которых число неизвестных реакций связей превышает возможное для них число уравнений равновесия статики. Число “лишних” неизвестных определяет степень их статической неопределимости.
Для расчета таких систем, кроме уравнений статики, необходимо составлять дополнительные уравнения, называемые уравнениями перемещений (или уравнениями совместимости деформаций системы). Их получают из рассмотрения условий деформации системы. Всегда можно составить столько дополнительных уравнений, чтобы полное число уравнений вместе с условиями статики равнялась числу неизвестных.
В инженерной практике известны несколько методов расчетов статически неопределимых систем: способ сравнения деформаций, уравнение трех моментов, метод сил, метод перемещений и др.
Во всех этих методах используется один и тот же принцип: рассматриваемая статически неопределимая система отбрасыванием “лишних” связей превращается в статически определимую. Полученную таким образом статически определимую систему называют основной системой, которую и рассматривают в дальнейших расчетах. Однако основная система имеет силовое и деформационное отличия от заданной статически неопределимой системы, которые необходимо устранить.
Силовое отличие устраняется путем приложения неизвестных реакций вместо отброшенных “лишних” связей. Такую систему называют эквивалентной. Деформационное отличие устраняется составлением канонических уравнений, исключающих перемещение системы по направлению отброшенной связи.
Рассмотрим решение методом сил однопролетной один раз статически неопределимой балки, показанной на рисунке 6.1.

Рис. 6.1. Схема однопролетной статически неопределимой балки
Требуется, например, для данной схемы определить реактивный момент, возникающий в заделке .
Выберем основную систему, соответствующую условиям эксперимента.
В данной задаче необходимо определить реактивный момент, поэтому оптимальным выглядит замена жесткой заделки на шарнирно-неподвижную опору, при которой система становится статически определимой.
Для
устранения силового отличия заданной
и основной систем (жесткая заделка
препятствует повороту сечения
балки, а шарнирная опора нет) в шарнире
основной системы прикладывается
дополнительный неизвестный момент
![]() .
.
Эквивалентная система для решения данной задачи представлена на рисунке 6.2.

Рис. 6.2. Эквивалентная система
Каноническое уравнение метода сил в этом случае имеет вид
![]() ,
,
где
![]() - перемещение точки приложения “лишнего”
неизвестного по его направлению,
вызванное действием единичного значения
этого неизвестного. В рассматриваемой
задаче это будет угол поворота сечения
балки на опоре
по направлению момента
в случае, когда
- перемещение точки приложения “лишнего”
неизвестного по его направлению,
вызванное действием единичного значения
этого неизвестного. В рассматриваемой
задаче это будет угол поворота сечения
балки на опоре
по направлению момента
в случае, когда
![]() ;
;
![]() -
перемещение точки приложения “лишнего”
неизвестного по его направлению,
вызванное действием заданной внешней
нагрузки. В рассматриваемой задаче это
будет угол поворота сечения балки на
опоре
по направлению момента
от действия силы
.
-
перемещение точки приложения “лишнего”
неизвестного по его направлению,
вызванное действием заданной внешней
нагрузки. В рассматриваемой задаче это
будет угол поворота сечения балки на
опоре
по направлению момента
от действия силы
.
Данное уравнение решим способом Верещагина, для чего построим эпюры изгибающих моментов от и внешней нагрузки (силы ). Полученные эпюры представлены на рисунке 6.3.

Рис.
6.3. Грузовая
![]() и единичная
и единичная
![]() эпюры моментов.
эпюры моментов.
По Верещагину перемещение балки может быть вычислено по формуле
![]() ,
,
где - площадь “первой” эпюры;
- ордината “второй” эпюры, взятая под центром тяжести “первой” эпюры;
![]() -
жесткость балки при изгибе.
-
жесткость балки при изгибе.
Тогда для рассматриваемой схемы получим:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
![]() ;
;
![]() .
.
После подстановки полученных результатов в каноническое уравнение будем иметь
![]() .
.
Тогда
неизвестный момент равен
![]() .
.
Знак
“+” говорит о том, что направление
реактивного момента совпадает с
направлением единичного момента
![]() .
.
