Опытная проверка теории изгиба прямого стержня

Цель работы: экспериментальное определение прогибов и углов поворота сечений, а также нормальных напряжений в прямом стержне при плоском поперечном изгибе и сравнение их с теоретическими значениями.

1. Краткие теоретические сведения

Стержень, работающий на изгиб, принято называть балкой.

При изгибе балки ее поперечные сечения, оставаясь плоскими, совершают перемещения двух типов: линейные и угловые. Угловые перемещения называют углом поворота сечения; линейные перемещения в направлении перпендикулярном продольной оси балки - прогибом; линейным перемещением вдоль продольной оси пренебрегают в силу его малости по сравнению с прогибом.

В пределах упругих деформаций прогибы и углы поворота величины малые.

Теоретически перемещения в балке могут определяться либо на основании дифференциального уравнения изогнутой оси балки, либо энергетическими методами. Энергетические методы (теорема Кастилиано, интеграл Мора, способ Верещагина) позволяют, сравнительно просто, определять перемещения нейтральной линии сечения.

Методы, построенные на использовании дифференциального уравнения изогнутой оси (метод непосредственного интегрирования, метод начальных параметров), позволяют получать уравнения перемещений и, следовательно, их эпюры.

1. Метод непосредственного интегрирования дифференциального уравнения изогнутой оси и метод начальных параметров

Рассмотрим плоский поперечный изгиб стержня с прямой осью и постоянными поперечными размерами. В случае малых прогибов перемещения сечений такого стержня определяются из приближенного дифференциального уравнения изогнутой оси

или , (5.1)

где - кривизна изогнутой оси;

- радиус кривизны;

- прогиб (перемещение в направлении оси ) сечения с координатой );

- уравнение изгибающего момента;

- жесткость при изгибе.

Выбор знака в выражении (5.1) зависит от выбора направления оси и правила знаков для изгибающего момента. Так, например, для случая, когда ось направлена вверх (рис. 5.1), положительному изгибающему моменту соответствует положительная кривизна и наоборот, отрицательному изгибающему моменту - отрицательная кривизна. Тогда в уравнении (5.1) следует принять знак плюс.

Если ось направлять вниз, то у кривизны и изгибающего момента будут различные знаки (рис. 5.1), и в выражении (5.1) следует принимать знак минус.

а)

б)

Рис. 5.1. Схема зависимости знаков и от направления оси

Последовательно интегрируя выражение (5.1), на каждом из участков нагружения балки, получим уравнения углов поворота и прогибов для каждого участка

, (5.2)

. (5.3)

Здесь, и в дальнейшем, принято направление осей по рисунку 5.1б (ось - на нас).

Постоянные интегрирования и определяются из условий неразрывности перемещений на границах участков.

В инженерных расчетах пользоваться методом непосредственного интегрирования дифференциального уравнения при большом количестве участков интегрирования сложно. В этом случае необходимо составлять и решать систему уравнений с постоянными интегрирования и , количество которых вдвое превышает количество участков нагружения.

При выполнении определенных правил удается количество постоянных интегрирования свести к двум начальным параметрам: , . Такой метод получил название метода начальных параметров.

В случае действия на балку сосредоточенных моментов и сил, а также равномерно распределенной нагрузки (рис. 5.2), уравнения метода начальных параметров имеют вид:

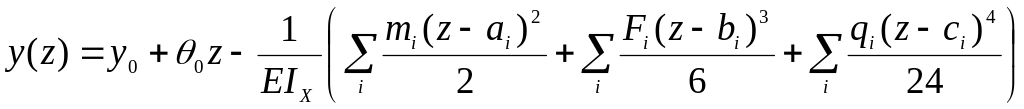, (5.4)

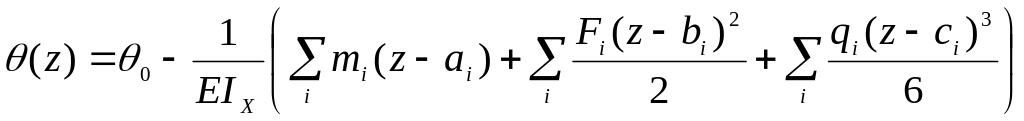. (5.5)

Здесь и - прогиб и угол поворота сечения в начале координат, совмещенном с крайним левым сечением балки; - расстояния от начала координат до сечений, в которых приложены нагрузки.

Рис. 5.2. Часть балки слева от рассматриваемого сечения с нагрузками

Начальные параметры определяются из условий закрепления балки.

Уравнения (5.4) и (5.5) записывают, обычно, для крайнего правого участка балки. При вычислении перемещений конкретных сечений в эти уравнения включают только те нагрузки, которые располагаются слева от сечения.

Нагрузки, направления которых совпадают с показанными на рисунке 5.2, подставляют в уравнения (5.4) и (5.5) со знаком плюс; противоположные - со знаком минус. Если распределенная нагрузка обрывается слева от сечения, то ее дополняют до сечения, одновременно прикладывая компенсирующую, противоположного направления и той же интенсивности.

Положительному прогибу соответствует перемещение в направлении оси , положительному углу поворота - поворот сечения по часовой стрелке.