Метод координат.

В аналитической геометрии геометрические объекты – кривые и поверхности – изучаются при помощи алгебры. В основе такого изучения лежит метод координат, при котором положение точки на прямой плоскости или в пространстве определяется соответственно одним, двумя или тремя числами, координатами этой точки, а каждой кривой или поверхности соответствует одно или несколько уравнений, связывающих координаты всякой точки им принадлежащей.

M 2,5

M (3;4)

M (1;3;2,5)

Подставим в уравнение.

½=1/2*1²(u) координаты точки M удовлетворяют уравнению y=(1/2)*x²

О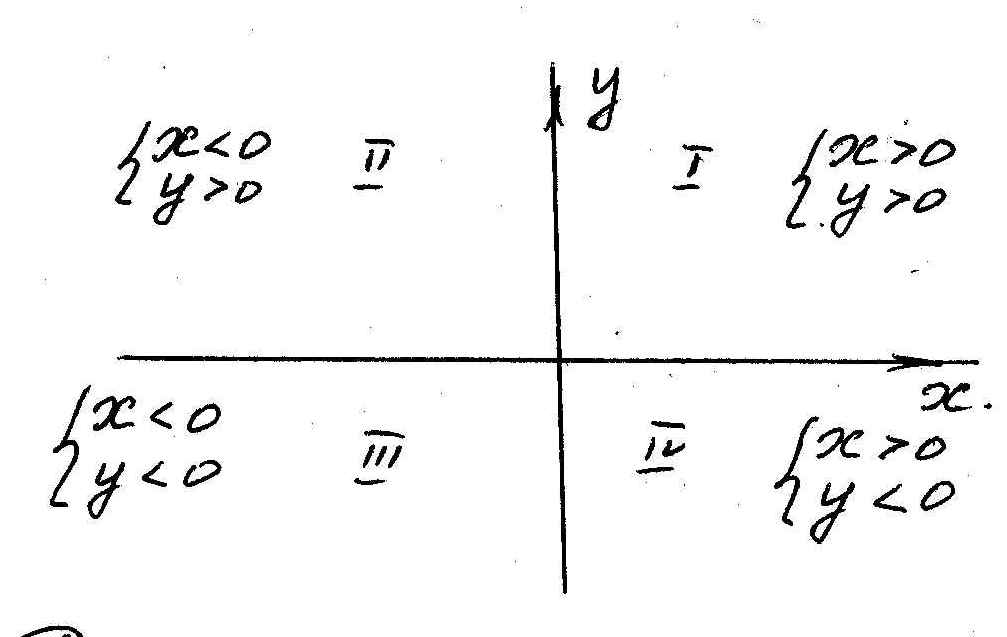 пределение. Абсциссой точки называют расстояние этой точки до оси (OY). Абсцисса положительна, если точка расположена справа от оси (OY), отрицательна, если точка слева от оси (OY).

Определение. Ординатой точки называют расстояние этой точки до оси (OX). Ордината положительна, если точка расположена выше оси (OX), отрицательна, если точка ниже оси (OX).

Р асстояние между двумя точками на плоскости.

Деление отрезка в заданном соотношении.

В ыберем точку О произвольно и зададим векторы:

Выразим вектор через и .

Из (2) подставим в (1)

Из имеем

из (4) – в (3)

(5)

поместим рисунок в систему координат так, чтобы точка О стала центром системы, тогда , координаты точки - неизвестны. Т.к. начало векторов ОА, ОВ, ОС – находятся в начале координат, то эти векторы называются радиус-векторами точек А, В, С (соответственно), тогда

Равенство (5) является векторной формулой деления отрезка в данном отношении.

Ч тобы получить координатные формулы необходимо подставить в (5) из (6) одноименные координаты.

*

Формулы координат точки С, делящей отрезок АВ в отношении (считая от А к В)Если отрезок АВ разделить точкой С на два равных отрезка, то

**

З адача 1

Н айти центр тяжести треугольника. Центр тяжести треугольника находиться в точке пересечения медиан. Находим координаты точки М₁ из условия:

Медианы в точке пересечения делятся в отношении

( от В к М₁)

Задача 2. До какой точки надо продлить отрезок АВ(от А к В) чтобы длина его стала в четыре раза больше прежней.

З адача 3.

М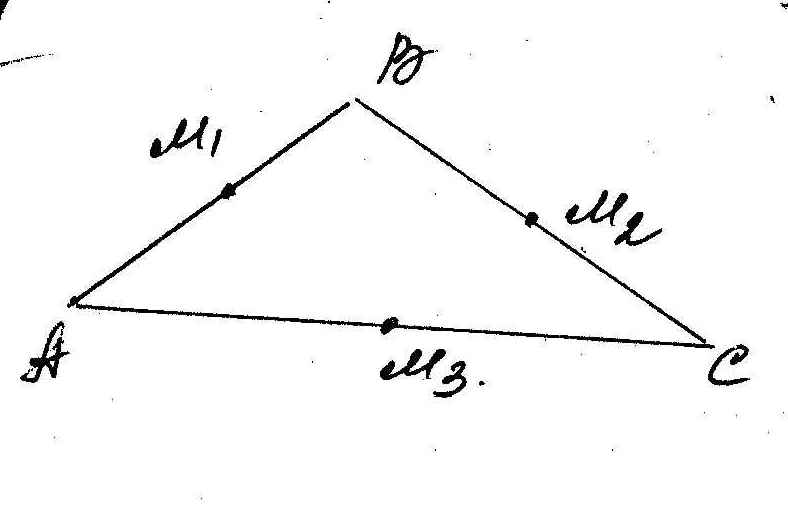 ₁ (2;-1)М₂ (-1;3) М₃ (-4;2) есть координаты середины сторон треугольника. Найти координаты вершин треугольника.

П усть

Тогда по формулам **

Определители второго порядка.

О

а₁₁ а₁₂

а₂₁ а₂₂

пределение: Выражение

= а₁₁•a₂₂-a₂₁•a₁₂ – называется определителем второго порядка.

а_11, a₁₂ – элементы первой строки

a₂₁,a₂₂ – элементы второй строки.

a_11, a₂₁ – элементы первого столбца

a_12, a₂₂ – элементы второго столбца

a_11, a₂₂ – элементы главной диагонали

a_12, a₂₁ – элементы побочной диагонали.

Определители обладают рядом свойств.

Определители третьего порядка.

Выражение вида:

а₁₁ а₁₂ а₁₃

а₂₁ а₂₂ а₂₃

а₃₁ а₃₂ а₃₃

=a₁₁ a₂₂ a₃₃+ a₁₂ a₂₃ a₃₁+ a₂₁ a₃₂ a₁₃ – a₃₁ a₂₂ a₁₃ - a₂₁ a₁₂ a₃₃ – a₃₂ a₂₃ a₁₁.

Теорема.

Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические заполнения.

а₁₁ а₁₂ а₁₃ …a_n

а₂₁ а₂₂ а₂₃ …a_2n

а₃₁ а₃₂ а₃₃ …a_4n

………………..

a_n1 a_n2 a_n3… a_4n

Определитель n-го порядка. Вычеркнем мысленно j – строку и i – ый столбец. На пересечении будет элемент a_ij, оставшийся определителем n-1 порядка умноженный на (-1)^i+j будет называться алгебраическим дополнением элемента a_ij, и обозначается А_ij. А оставшийся определитель n-1 порядка называется минором (M_ij) элемента, a_ij. И тогда: A_ij=(-1)^i+j M_ij.

Пример.

Р

а₁₁ а₁₂ а₁₃

а₂₁ а₂₂ а₂₃

а₃₁ а₃₂ а₃₃

азложить определитель по элементам первой строки.

=