2. Лабораторная работа по теме: «Логические вычисления»

Целью данной лабораторной работы является изучение логических функций Excel, освоение способов построения логических выражений, описывающих геометрическое место точек, разработка разветвляющихся алгоритмов разной сложности, применение логических функций в табличных данных.

Теоретическая справка. Для использования логических функций Excel следует вспомнить некоторые простые понятия из математической ло­гики:

• Логическая величина — это величина, которая может принимать только одно из двух значений: либо ИСТИНА, либо ЛОЖЬ.

• ИСТИНА, ЛОЖЬ — логические константы.

• Высказывание — утверждение, относительно которого можно заключить, верно оно или нет, истинно или ложно (например, результатом высказывания 5 > 3 будет логическая величина – ИСТИНА).

• Предикат — высказывание с пере­менными; в зависимости от значения переменных предикат может принимать значения ИСТИНА или ЛОЖЬ (например, результатом предиката Х > 5 будет логическая величина – ИСТИНА, если Х = 10, и ЛОЖЬ, Х = 3).

• Логическое выражение — простое или сложное высказывание или предикат (например: b² – 4ac ≠ 0).

• Логические операции — операции, которые объединяют сложные логические выражения.

Основные логические операции:

• Конъюнкция (логическое умножение)

Записывается так: A  B, A И B, A & B, где А и В – логические величины (значения логических выражений).

Значение такого выражения будет ИСТИНА, если А и В истинны

(например: (x ≥ 10)  (x ≤ 100) – значение x в диапазоне от 10 до 100).

• Дизъюнкция (логическое сложение)

Записывается так:

AB, A ИЛИ B, где А и В – значения логических выражений.

Значение выражения будет ИСТИНА, если значение хотя бы одного из выражений (А, В) истинно (например: выражение (x < 10)  (x > 100) определяет значение x вне отрезка [10; 100]).

• Отрицание

Записывается: НЕ А, А, где А – значение логического выражения.

Значение выражения изменяется на противоположное

(например: A = b > 4, А =  (b > 4) = b ≤ 4, b не больше 4).

Структура логического выражения:

• логические константы;

• предикаты и высказывания (сравнения), которые могут содержать арифметические выражения;

• логические операции;

• скобки.

П риоритет операций в логическом выражении:

1	Алгебраические выражения
2	Сравнения (отношения)
3	Логические операции:
1)	– отрицание
2)	– конъюнкция
3)	– дизъюнкция

Так как логические переменные могут принимать только два значения ИСТИНА или ЛОЖЬ, то логические операции можно задать таблицей, где перечислены все возможные значения аргументов и соответствующие им результаты операций (таблицы истинности):

А	В	А И В	А ИЛИ В	НЕ А
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ЛОЖЬ	ИСТИНА
ЛОЖЬ	ИСТИНА	ЛОЖЬ	ИСТИНА	ИСТИНА
ИСТИНА	ЛОЖЬ	ЛОЖЬ	ИСТИНА	ЛОЖЬ
ИСТИНА	ИСТИНА	ИСТИНА	ИСТИНА	ЛОЖЬ

Примеры записи логических выражений в Excel:

	Математическая запись	Excel
1.	x·y – 6 ≠ 2·z	=A4*A3 – 6 < > 2 * B1
2.	(x ≥ 10)  (x ≤ 100)	=И ( А1>= 10; А1<= 100)
3.	(x ≤ 10)  (x ≥100)	=ИЛИ ( А1 < 10; А1 > 100)
4.	 (b > 4)	=НЕ ( B1 > 4 )

Примечания.

1. Ввод логической формулы, как обычно, начинается со знака “=”.

2. Логические операции реализуются в Excel в виде логических функций (Категория  Логические):

Математическая запись	В Excel
А ^ В	И(А;В)
А  В	ИЛИ(А;В)
А	НЕ(А)

На практике логические выражения используются для разработки разветвляющегося алгоритма (развилки):

Алгоритмический язык Если условие (логическое выражение) т о д ействие 1 иначе д ействие 2 всё-если;

Б лок-схема

Для построения развилки в Excel существует логическая функция ЕСЛИ, структура её такова: ЕСЛИ (логическое выражение; оператор 1; оператор 2)

Если значение логического выражения ИСТИНА,

то выполняется оператор 1,

иначе выполняется оператор 2.

Р 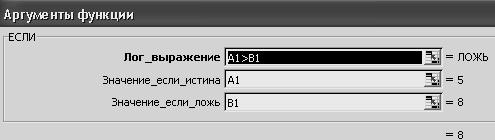ис. 5.

Пример задания аргументов функции ЕСЛИ

(нахождение максимального значения из двух чисел)