3. Решение систем линейных уравнений

м етодом обратной матрицы

Задание. Решить систему линейных уравнений методом обратной матрицы:

Методические указания к выполнению задания

1. Заданная система уравнений имеет вид AX=B, откуда решение: X=A^-1B, где А – матрица коэффициентов, а В – вектор свободных членов.

2. Ввести матрицу А в блок B2:D4 (рис.20); вектор В в блок G2:G4; задать имена указанным блокам.

3. Ввести формулу массива для вектора Х: {=МУМНОЖ(МОБР(A);B)}

в блок B6:B8.

4. Выполнить проверку: АХ=В; ввести блок F6:F8 формулу массива:

{=МУМНОЖ(A; B6:B8)}.

5. Решение – вектор Х – верное, т.к. при подстановке Х в систему уравнений получаются тождества.

6. Варианты заданий по этой теме см. 6.5.3.

Рис.20. Решение системы линейных уравнений (пример 6.3.)

4. Вычисление матричных выражений

З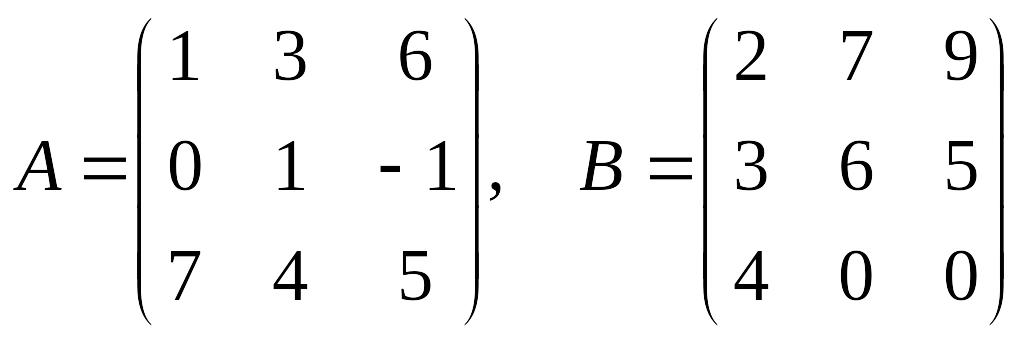 адание. Выполнить операции над матрицами:

Найти (A + B)(A - B) -A², где

Методические указания к выполнению задания

1. Ввести матрицу А в блок B1:D3, матрицу В – в блок F1:H3;

задать имена указанным блокам.

2. Вычислить заданное матричное выражение, разбивая его на части по методу последовательной детализации:

• ввести формулу массива: { = A + B } в блок B5:D7;

• ввести формулу массива: { = A - B } в блок F5:H7;

• ввести формулу массива: (A + B)(A - B):

{=МУМНОЖ(B5:D7;F5:H7)} в блок B9:D11;

• ввести формулу массива A²: {=МУМНОЖ(B1:D3;B1:D3)}

в блок F9:H11.

3. Результирующую формулу: {=B9:D11 - F9:H11} ввести в блок C13:E15.

4. В арианты заданий по этой теме см. 6.5.4.

Рис.21. Вычисление матричных выражений (пример 6.4.)

5. Скалярное произведение векторов

Задание. Вычислить скалярное произведение: (a + b, a - b), если

a = (1; 1; 0,5; 6; -2) , b = (0; 3; -1,5; 0; 1,9)

Методические указания к выполнению задания

1. Ввести вектор а в блок B1: F1, вектор b – в блок В2: F2 (рис. 22);

задать имена указанным блокам;

2. Вычислить вектор а + b по формуле массива: {=B1:F1+B2:F2} или {=а+в};

3. Вычислить вектор а - b по формуле массива: {=B1:F1- B2:F2} или {=а-в};

4. Вычислить скалярное произведение полученных векторов:

{=СУММ(B4:F4*B5:F5)} или {=СУММ((а+в)*(а-в))}.

5. Варианты заданий по этой теме см. 6.5.2.

Рис.22.

Вычисление скалярного произведения векторов (пример 6.5.)

1. Применение скалярного произведения в экономических задачах

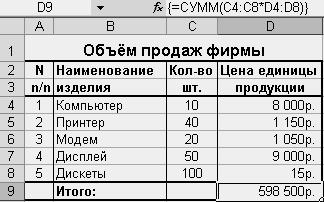
Пример 1. Дана таблица объёма продаж фирмы (Рис. 23). Подсчитать объёмы прибыли фирмы.

В ыполнение:

1. Объёмы прибыли фирмы

(общая стоимость всех изделий)

вычисляются по формуле

скалярного произведения векторов:

, где

кол_во - вектор значений объёма продаж;

цена - вектор значений цены Рис.23. Таблица объёма продаж фирмы

изделия.

2. Ввести формулу массива в ячейку D9: {= СУММ(С4:С8* D4:D8)}

(или {= СУММ(кол_во* цена)});

Пример 2. Дана таблица реализации печатной продукции:

N книг	Количество, шт.			Цена за ед. продукции, руб.
n/n	январь	февраль	март	январь	февраль	март
1	12000	15000	10000	85	90	100
2	10000	11000	10000	50	65	60
3	3000	5000	2000	70	72	75
4	20000	15000	10000	85	86	90
5	5000	3000	7000	40	45	47

Подсчитать прибыль за квартал.

Выполнение:

1. Формула вычисления:

Прибыль за квартал = , где

i - n/n автора и книги, j - номер месяца,

Количество – матрица значений количества проданной продукции

за 3 месяца;

Цена – матрица значений цены проданной продукции за 3 месяца.

2. Ввести формулу массива: {=СУММ(Кол_во*Цена)} в ячейку результата.

3. Проверить результат другим способом:

• добавить в таблицу столбец "Стоимость";

• поместить в этот столбец результат скалярного произведения вектора "Количество" и вектора "Цена" для каждой книги

• найти общую стоимость всех книг автосуммированием.

Сравнить результаты обоих способов.