2. Решение нелинейного уравнения

приближённым способом с заданной точностью

Напоминание из курса математики:

1. Пусть f(x) = 0 – некоторое уравнение. Число х = η называется корнем, или решением данного уравнения, если подстановка его в уравнение обращает его в тождество, т.е. f(η) ≡ 0.

2. Корнями уравнения f(x)=0 являются абсциссы точек пересечения кривой y=f(x) с осью Ох.

3. Если функция y=f(x) непрерывна и принимает на концах отрезка [a;b] значения разных знаков, т.е. f(a)f(b)<0, то внутри этого промежутка найдется нуль функции, т.е. корень уравнения f(x) = 0.

4. Приближённое решение уравнения f(x) = 0 состоит из двух этапов:

• нахождение грубо приближённых значений корней;

• уточнение найденных грубых приближений.

5. Метод последовательного приближения к значению корня с заданной точностью называется методом итераций.

Алгоритм решения нелинейного уравнения f(x) = 0 приближённым

(таблично- графическим) способом с заданной точностью ε:

1. отделить корень - установить промежуток [a;b] из области определения f(x),

в котором могут быть корни уравнения f(x) = 0;

2. протабулировать функцию y = f(x) в этом отрезке (см. 5.1);

3. построить график функции по полученным табличным значениям;

4. по таблице значений функции определить отрезок [x_i; x_i+1], (i=1..n) на концах которого функция y = f(x) принимает значения разных знаков

(этот же отрезок можно установить по графику – это отрезок, в котором график пересекает ось Ох). В этом отрезке содержится х, в котором f(x)=0

(см. Напоминание – теорема 3).

5. Если не будет достигнута требуемая точность, т.е. |f(x)|> ε,

уточнить корень: задать новые значения а= x_i и b= x_i+1, вернуться к шагу 4). Повторяя этот процесс («итерируя») несколько раз, получить значение корня х с заданной точностью, т.е. |f(x)| ≤ ε,

1. П ример выполнения задания: «Решение нелинейного уравнения»

Задание. Решить уравнение таблично-графическим

способом с точностью  = 0,0001.

Методические указания к выполнению задания

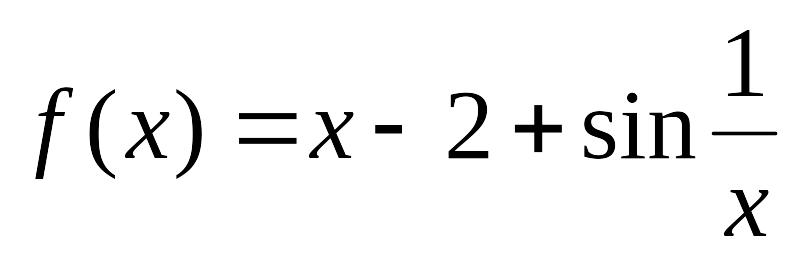1. О пределить приближенные значения отрезка Ох, в котором могут быть корни заданного уравнения, исходя из области определения функции

н апример: [0,5;3] (см. пример 5.1.1.).

2. Протабулировать функцию в этом отрезке (рис.15).

3. Из анализа табличных данных следует, что f(x) меняет знак в интервале между [1,25;1,5], т.е. здесь имеется корень уравнения, но значение этого корня не удовлетворяет заданной точности: f(x)=|0,03| >  = 0,0001.

4. Построить график функции по полученным табличным значениям (рис.15).

Из графика также следует, что f(x) в выбранном отрезке [0,5;3] имеет один корень, а именно в отрезке между 4-ой и 5-ой точками ([1,25;1,5]).

5. Уточнить корень:

• задать значения а=1,2; b=1,4;

• проанализировать изменения в графике и табличных значений – получается корень х=1,3 с точностью f(x)=-0,007;

• п олученная точность больше заданной, потому задать новые значения a=1,306; b=1,308, результат: f(x)=-0.00004 при х=1,30760 (рис.16).

Р ис.16. Решение нелинейного уравнения (пример 5.2.1)