1.9. Взаимное расположение прямых линий

Прямые линии в пространстве могут быть параллельны, пересекаться или скрещиваться.

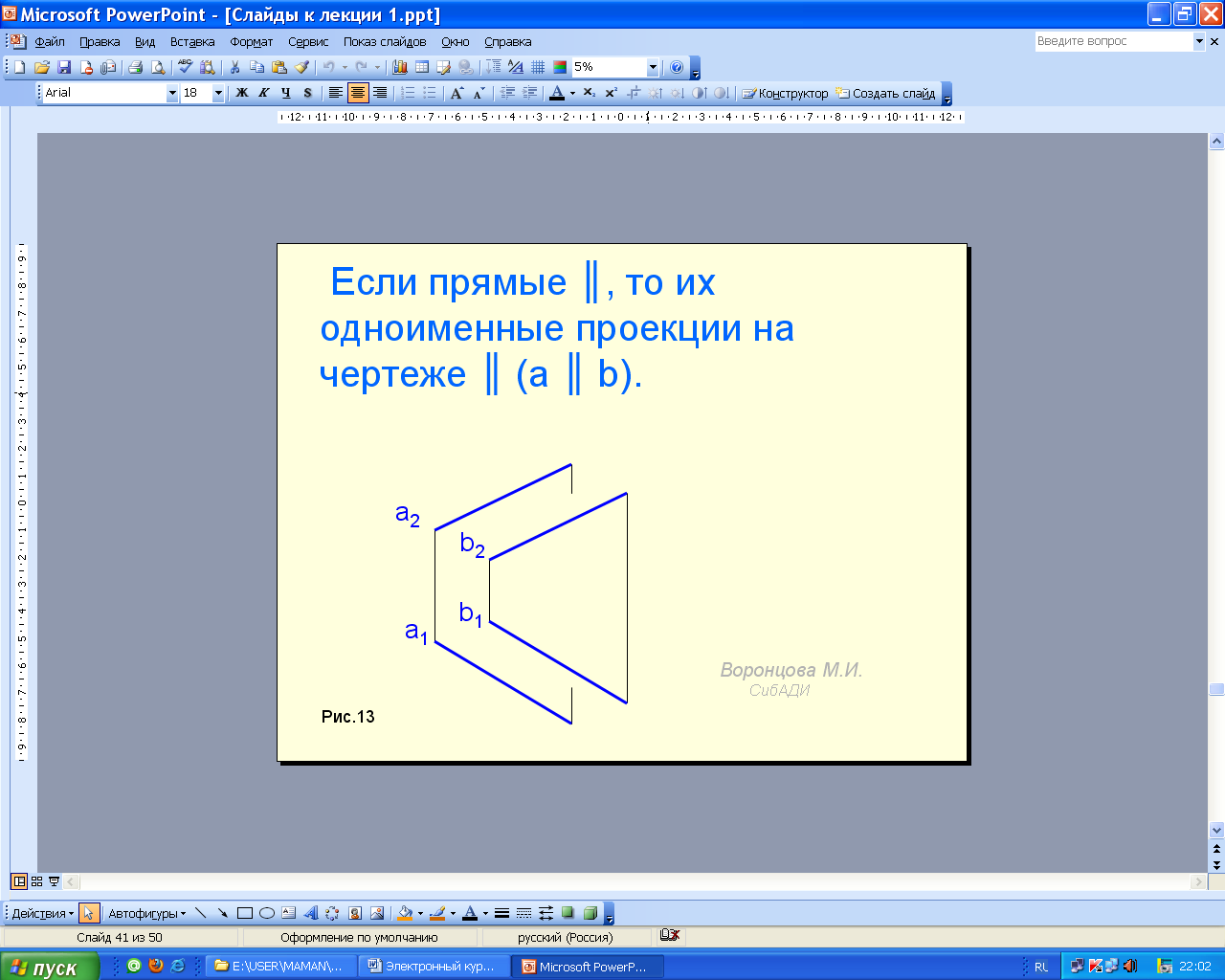Если прямые параллельны, то их одноименные проекции на чертеже параллельны (рис. 1.19).

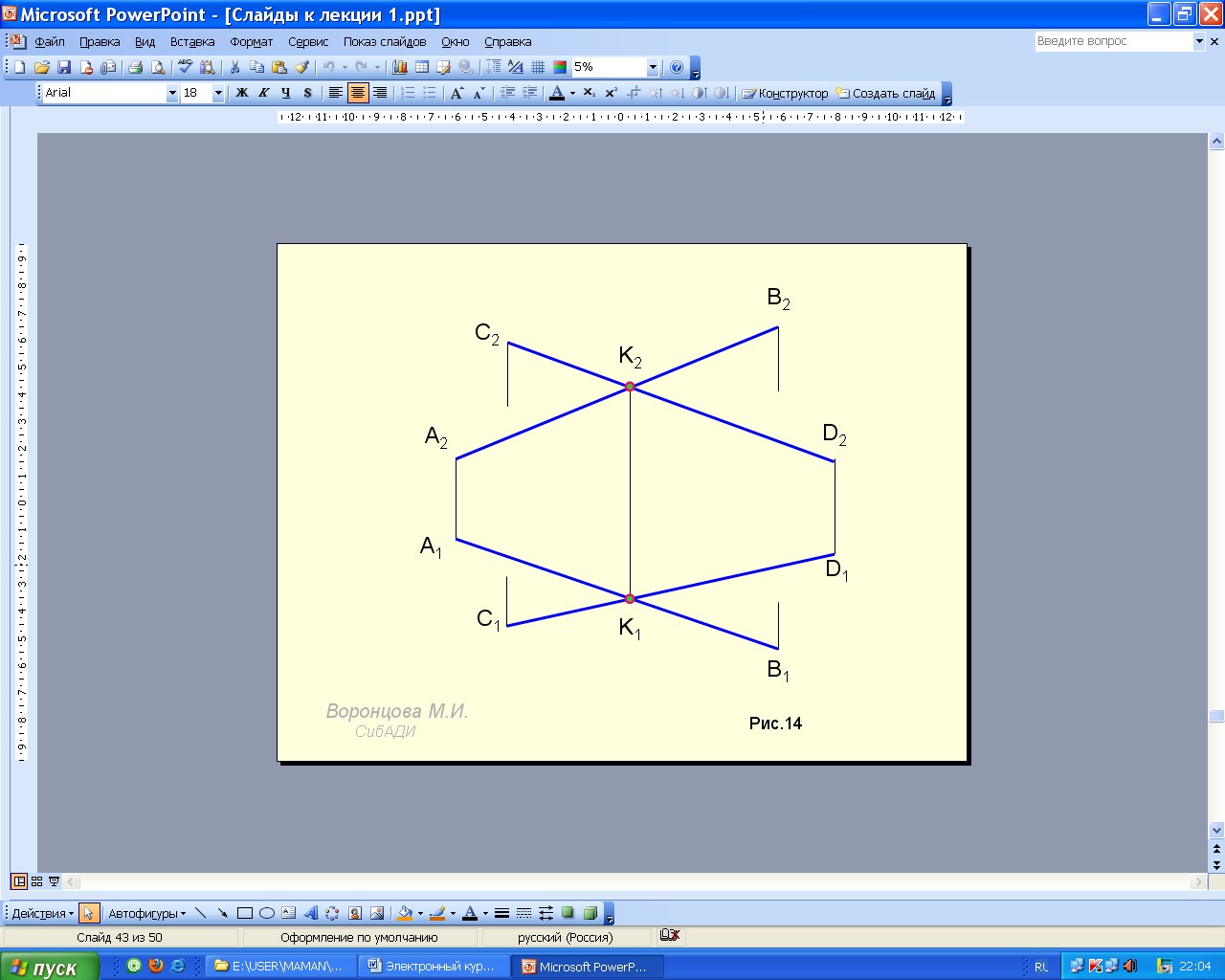
Если прямые пересекаются, то на чертеже проекции их точки пересечения лежат на одной линии связи (рис. 1.20).

Анимации/Рис.1.19. Параллельные прямые.exe

Анимации\Рис.1.20. Пересекающиеся прямые.exe

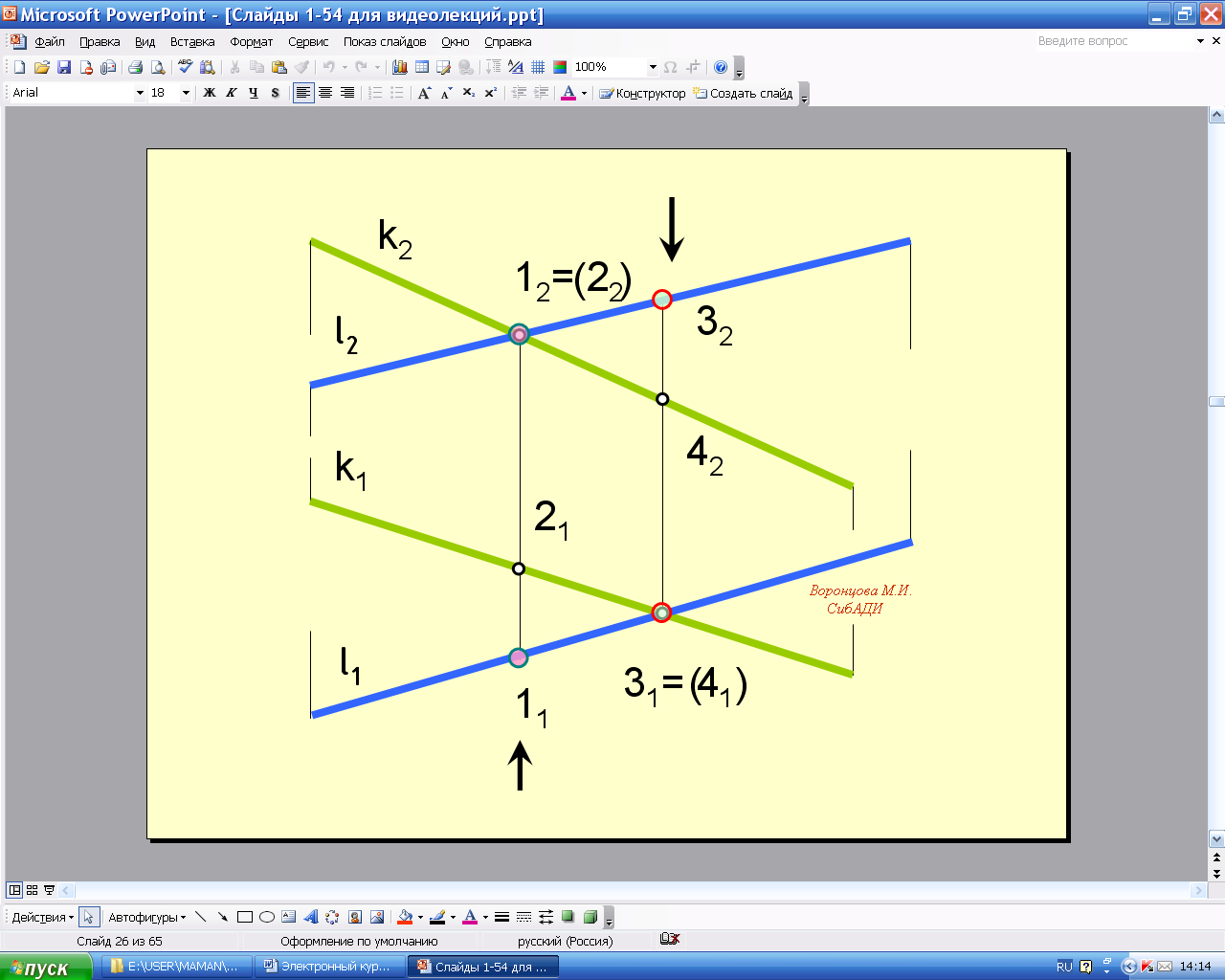
Если прямые не пересекаются и не параллельны, то они скрещиваются. У скрещивающихся прямых на одной из проекций совпадают проекции двух точек, поэтому одна из совпадающих точек становится закрытой. Такие точки называют конкурирующими (рис. 1.21).

1 и 2 (1₂=2₂) - фронтально–конкурирующие точки;

3 и 4 (3₁=4₁) - горизонтально–конкурирующие точки.

Анимации\Рис.1.21. Скрещивающиеся прямые.exe

Из двух горизонтально-конкурирующих точек на чертеже видимой будет та, фронтальная проекция которой расположена выше; из двух фронтально-конкурирующих точек видимой будет та, горизонтальная проекция которой будет ниже.

Точки 2 и 3 – невидимые (закрытые), 1 и 4 – видимые (открытые).

1.10. Проекции прямого плоского угла.

Если плоскость прямого угла не перпендикулярна к плоскости проекций, но хотя бы одна его сторона параллельна плоскости проекций, то на эту плоскость угол будет проецироваться в натуральную величину (рис. 1.22). На рис. 1.22, a угол АВС прямой, так как его сторона ВС является фронталью, а на рис. 1.22, á угол СDЕ не равен 90, так как обе стороны угла – прямые общего положения.

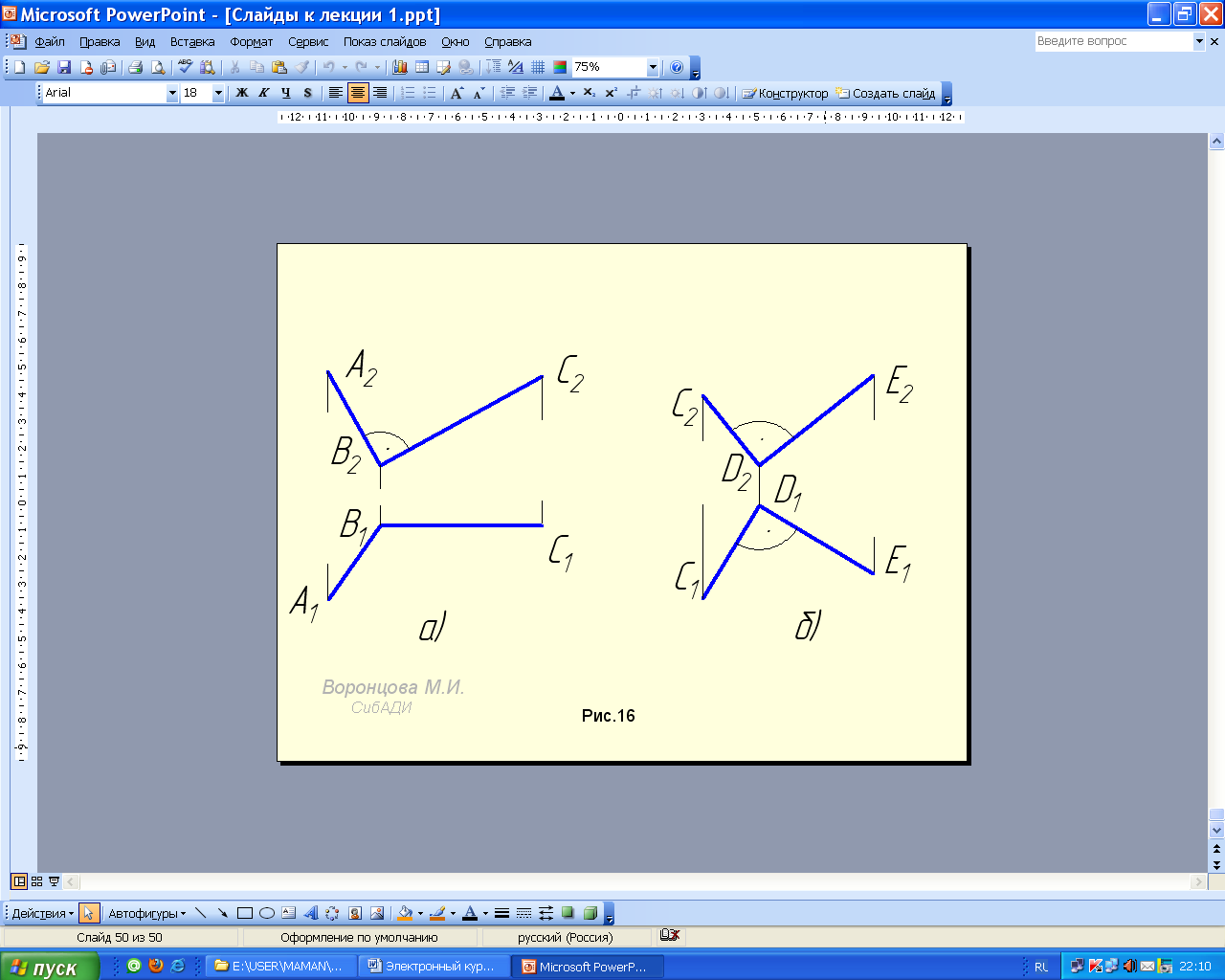
Рис. 1.22. Проекции плоских углов

Вопросы для самопроверки

1. Что понимают под проецированием?

2. В чем состоит сущность центрального проецирования?

3. В чем состоит сущность параллельного проецирования?

4. В чем заключается метод Монжа?

5. Что называют проекциями точки?

6. Какие линии называют линиями связи?

7. Какой чертеж называют комплексным?

8. Как связаны между собой горизонтальная и фронтальная проекции точки? Фронтальная и профильная?

9. Что называют координатами точки?

10. Какие координаты на эпюре определяют горизонтальную,

фронтальную и профильную проекции точки?

11. Какие прямые называют прямыми общего положения? Уровня? Проецирующими?

12. Как определить натуральную величину отрезка прямой обще-

го положения способом прямоугольного треугольника?

13. Что называется следами прямой линии?

14. Как определить на чертеже прямые параллельные, пересекающи-

еся и скрещивающиеся?

15. Какие точки называются конкурирующими? Как определить их ви-

димость на чертеже?

16. При каких условиях прямой плоский угол проецируется на плоскость проекций в натуральную величину?

2. Проекции плоскости. Прямая и точка в плоскости