5.3. Линейчатые поверхности с двумя направляющими и плоскостью параллелизма (поверхности Каталана)

Для задания этих поверхностей на комплексном чертеже достаточно указать проекции направляющих m и n и положение плоскости параллелизма .

Поверхность прямого цилиндроида образуется перемещением прямой линии l по двум криволинейным направляющим, не принадлежащим одной плоскости. При этом образующая прямая остается параллельной некоторой заданной плоскости, называемой плоскостью параллелизма. На рис. 5.60 изображен цилиндроид, направляющими которого являются кривые m (m₁, m₂) и n (n₁, n₂), а плоскостью параллелизма - плоскость (₁)  П₁, а также показано построение проекций точки А на поверхности цилиндроида.

Поверхность прямого коноида образуется перемещением прямой линии l по двум направляющим, одна из которых - кривая, а вторая - прямая линия. При этом образующая прямая остается параллельной некоторой заданной плоскости параллелизма. На рис. 5.61 изображен коноид, направляющими которого являются кривая m (m₁, m₂) и прямая n (n₁, n₂), а плоскостью параллелизма - плоскость (₁)  П₁, а также показано построение проекций точки А на поверхности коноида.

_{Гиперболический параболоид (косая плоскость) образуется перемещением прямой линии l по двум направляющим – скрещивающимся прямым линиям – параллельно некоторой плоскости параллелизма. Косая плоскость, направляющими которой являются скрещивающиеся прямые m(m1, m2) n(n1, n2) а плоскостью параллелизма – плоскость (1)} П₁, приведена на рис. 5.62, здесь же приведено построение проекций точки А на поверхности косой плоскости.

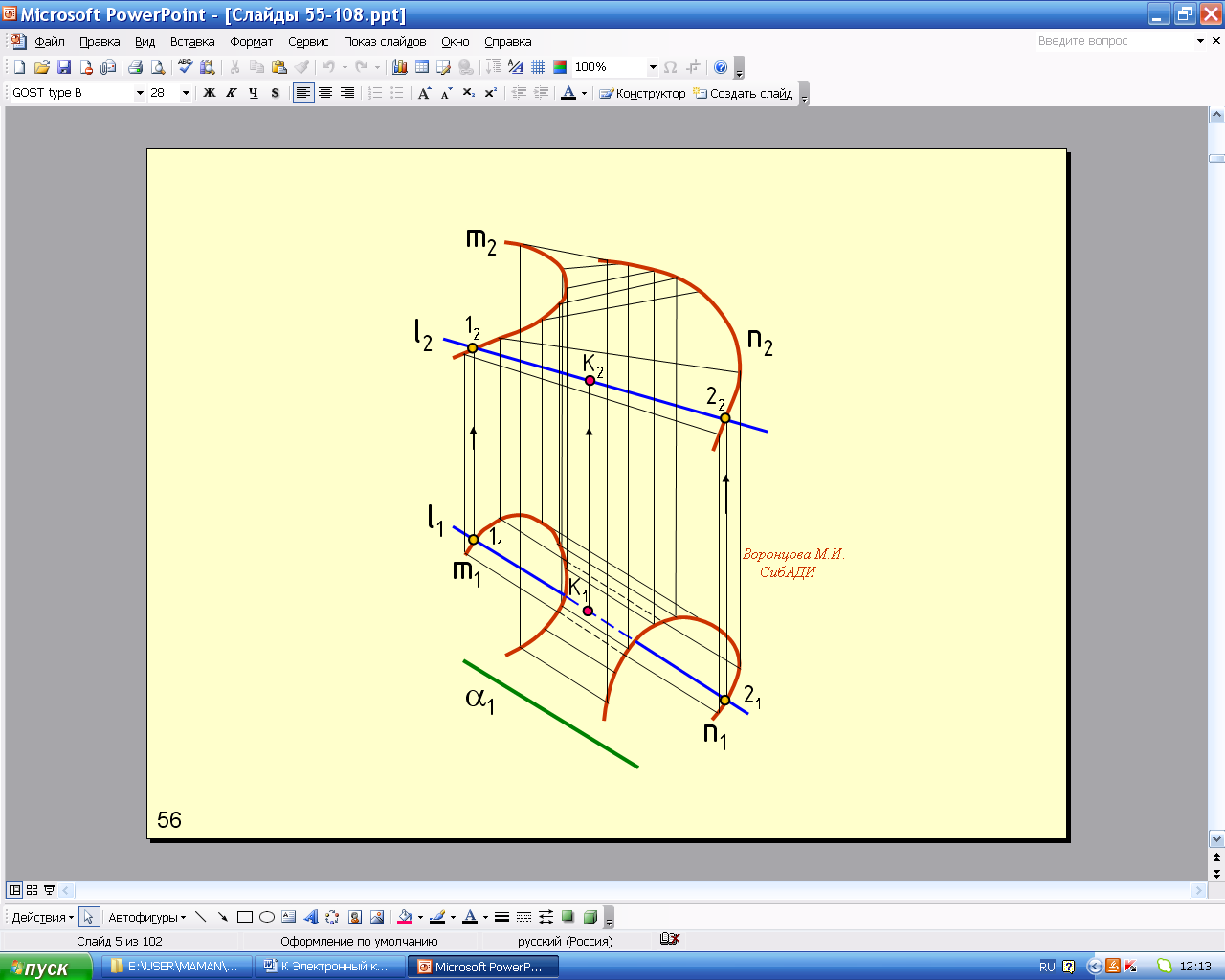
Анимации\Рис.5.60. Комплексный чертеж цилиндроида.exe

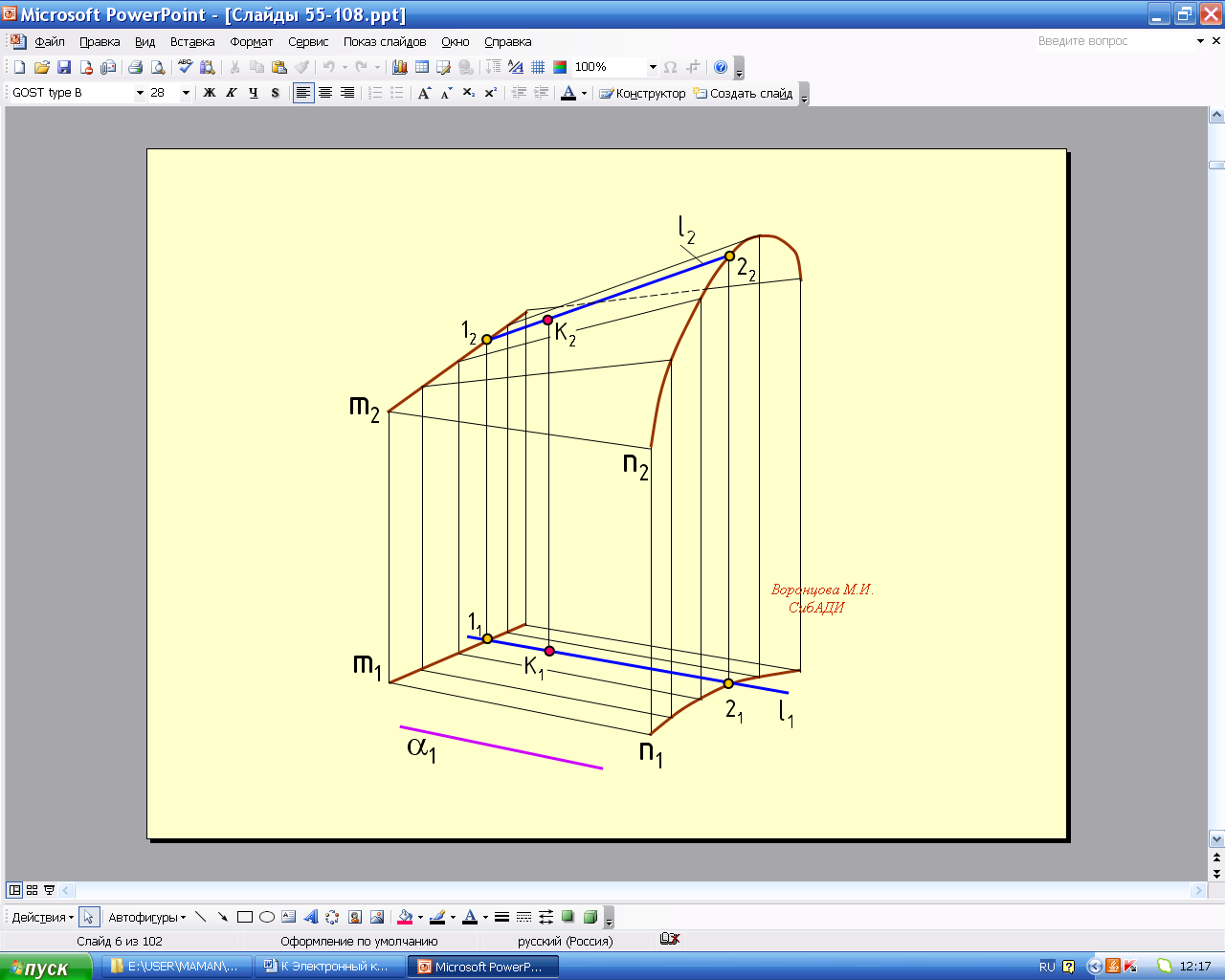
Анимации\Рис.5.61. Комплексный чертеж коноида.exe

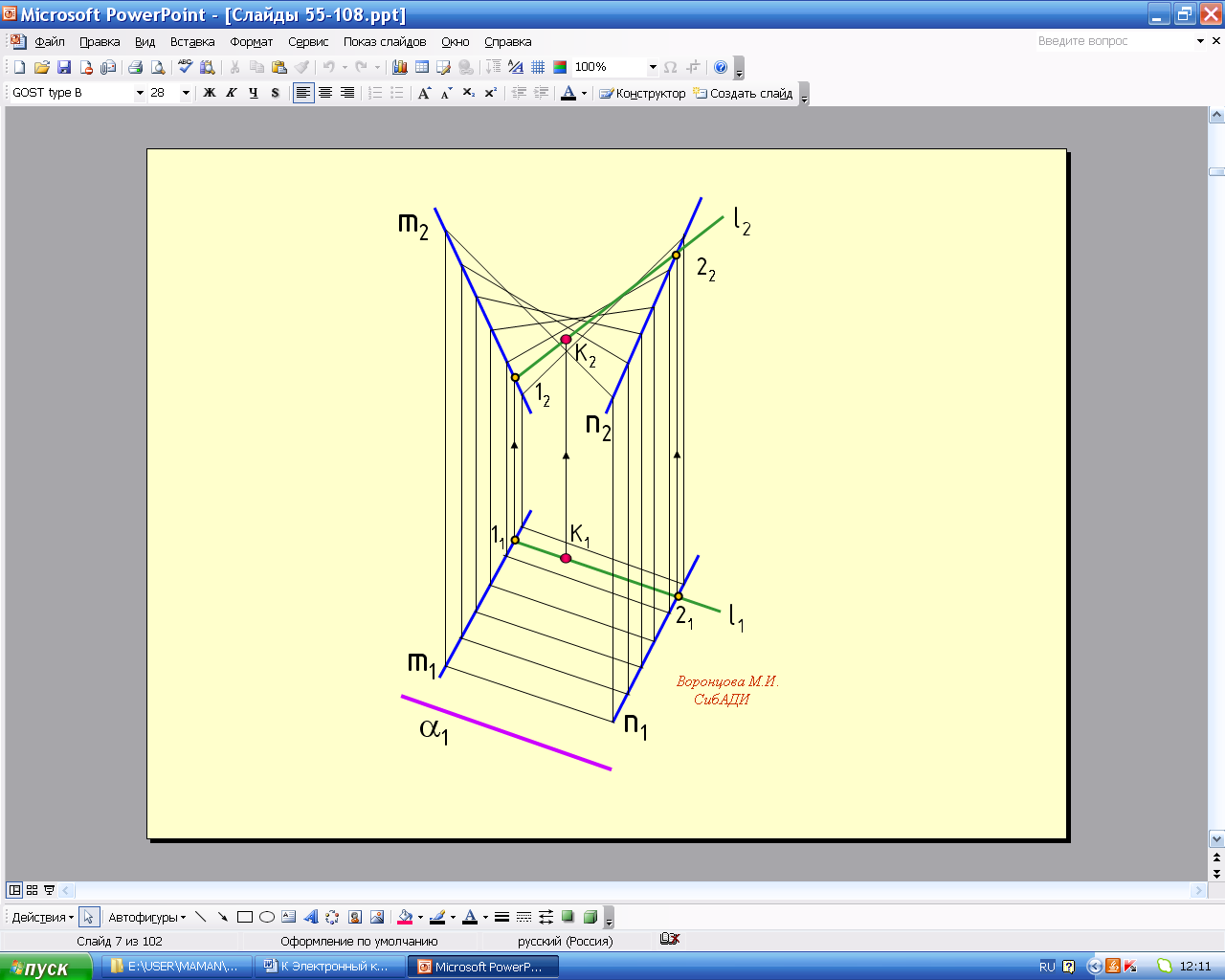
Анимации\Рис.5.62. Комплексный чертеж гиперболического параболоида (косой плоскости).exe

Гиперболический параболоид может быть получен перемещением параболы ВОВ₁, когда её ось симметрии остается параллельной оси z, а вершина перемещается вдоль параболы АОА₁ и плоскость параболы ВОВ₁ остается параллельной плоскости xoz. (рис. 5.63). В пересечении гиперболического параболоида плоскостью параллельной плоскости xoу получаются гиперболы, если такая плоскость проходит через вершину О. С этим связано название «гиперболический параболоид».

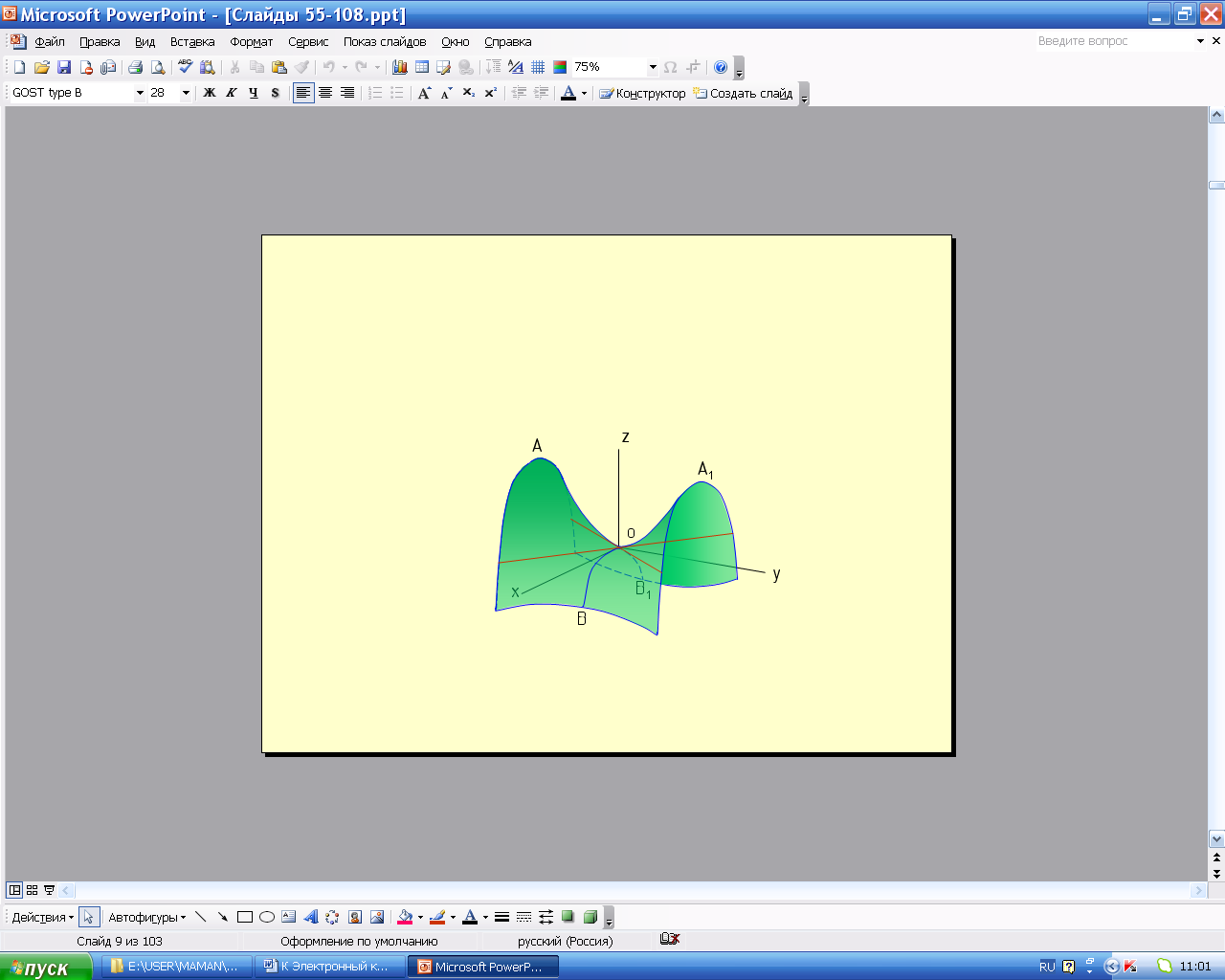
5.63. Модель гиперболического параболоида

5.4. Поверхности вращения

Поверхностью вращения называют поверхность, получаемую вращением какой-либо образующей линии вокруг неподвижной прямой - оси поверхности. Поверхность вращения можно задать образующей и положением оси; каждая точка образующей описывает окружность (рис. 5.64).

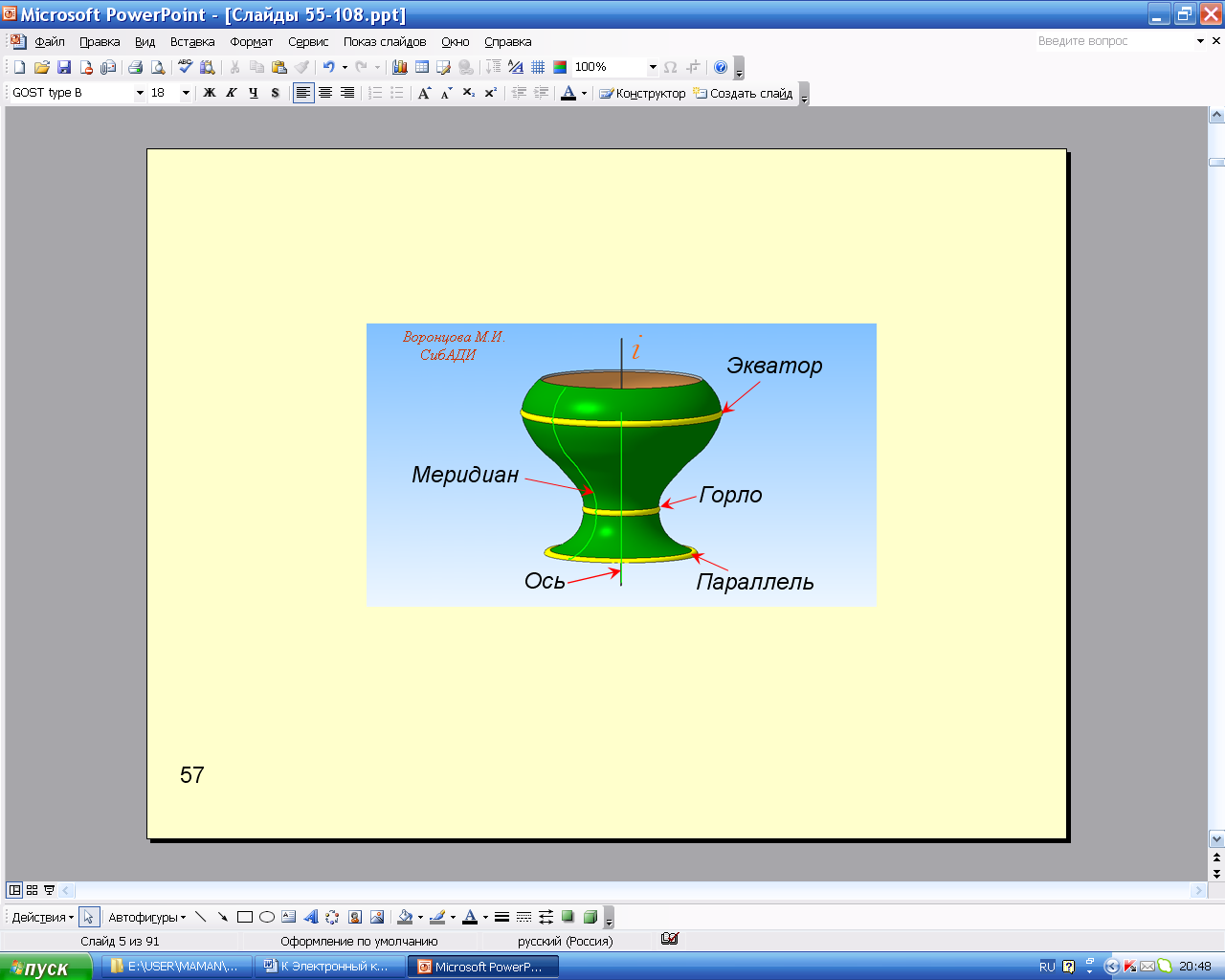
Рис. 5.64. Названия элементов поверхности

вращения общего вида

Плоскость, перпендикулярная к оси вращения, пересекает поверхность по окружности. Такие окружности называют параллелями. Наибольшая параллель называется экватором, наименьшая – горлом. Плоскость, проходящая через ось вращения, называется меридиональной; линии, по которым эта плоскость пересекает поверхность вращения, называют меридианами.

Образование поверхности вращения показано на рис. 5.65.

i – ось вращения, l – образующая.

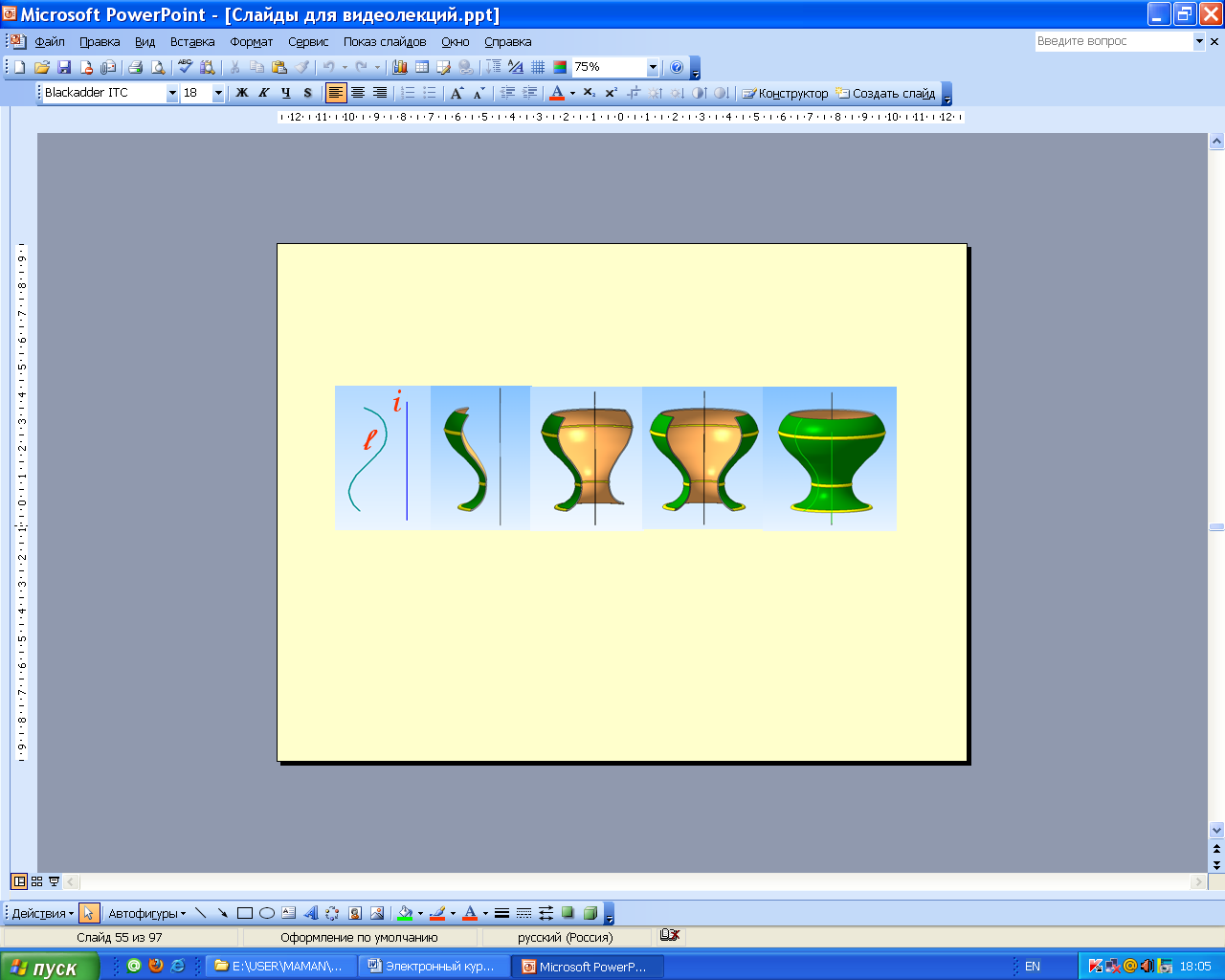
Рис. 5.65. Образование поверхности вращения

Наиболее распространенные поверхности вращения:

цилиндр вращения, конус, сфера, тор и др.

1.Цилиндр – часть цилиндрической поверхности, ограниченной двумя плоскостями. Он может быть круговым и эллиптическим. На рис. 5.66 приведены названия элементов цилиндра вращения. На рис. 5.67 показаны модель и чертеж построения проекций точки на поверхности цилиндра.

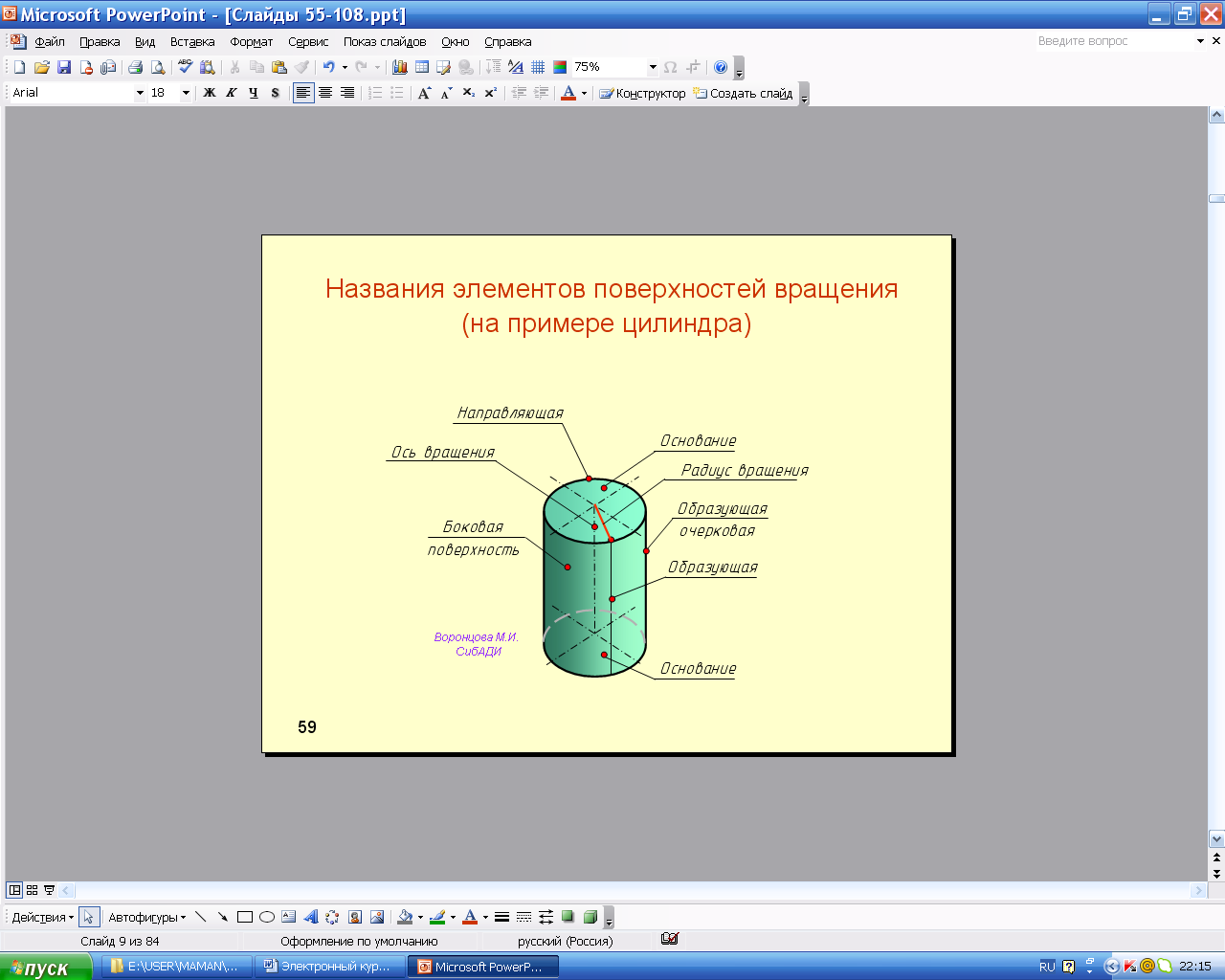
Анимации\Рис.5.66. Элементы поверхностей вращения геометрических тел.exe

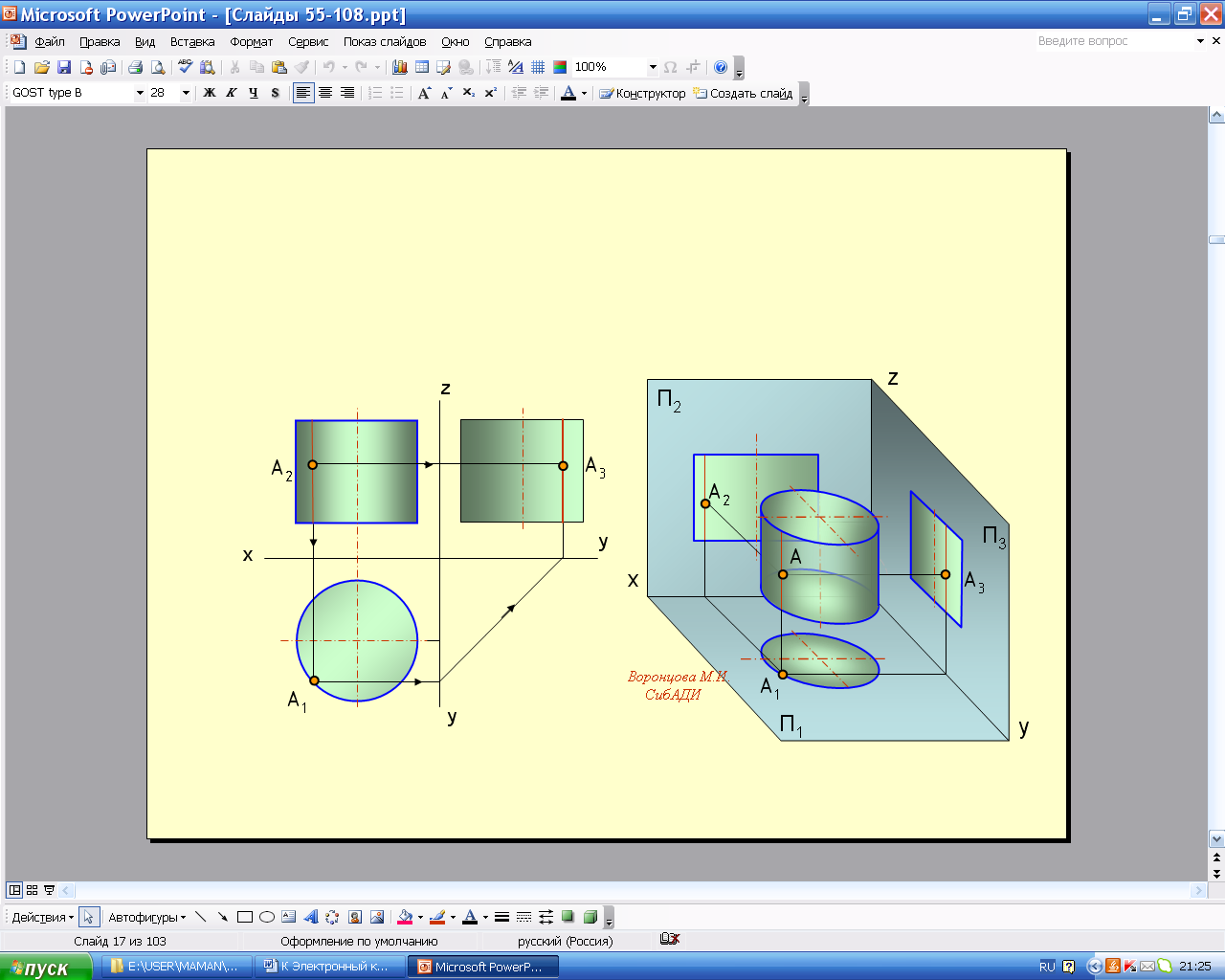
Анимации\Рис.5.67. Построение проекций точки на поверхности цилиндра.exe

3. Конус – часть конической поверхности, ограниченной одной

плоскостью. Основание конуса может быть круговым или эллиптическим. На рис. 5.68 показаны модель и чертеж построения проекций точки на поверхности конуса.

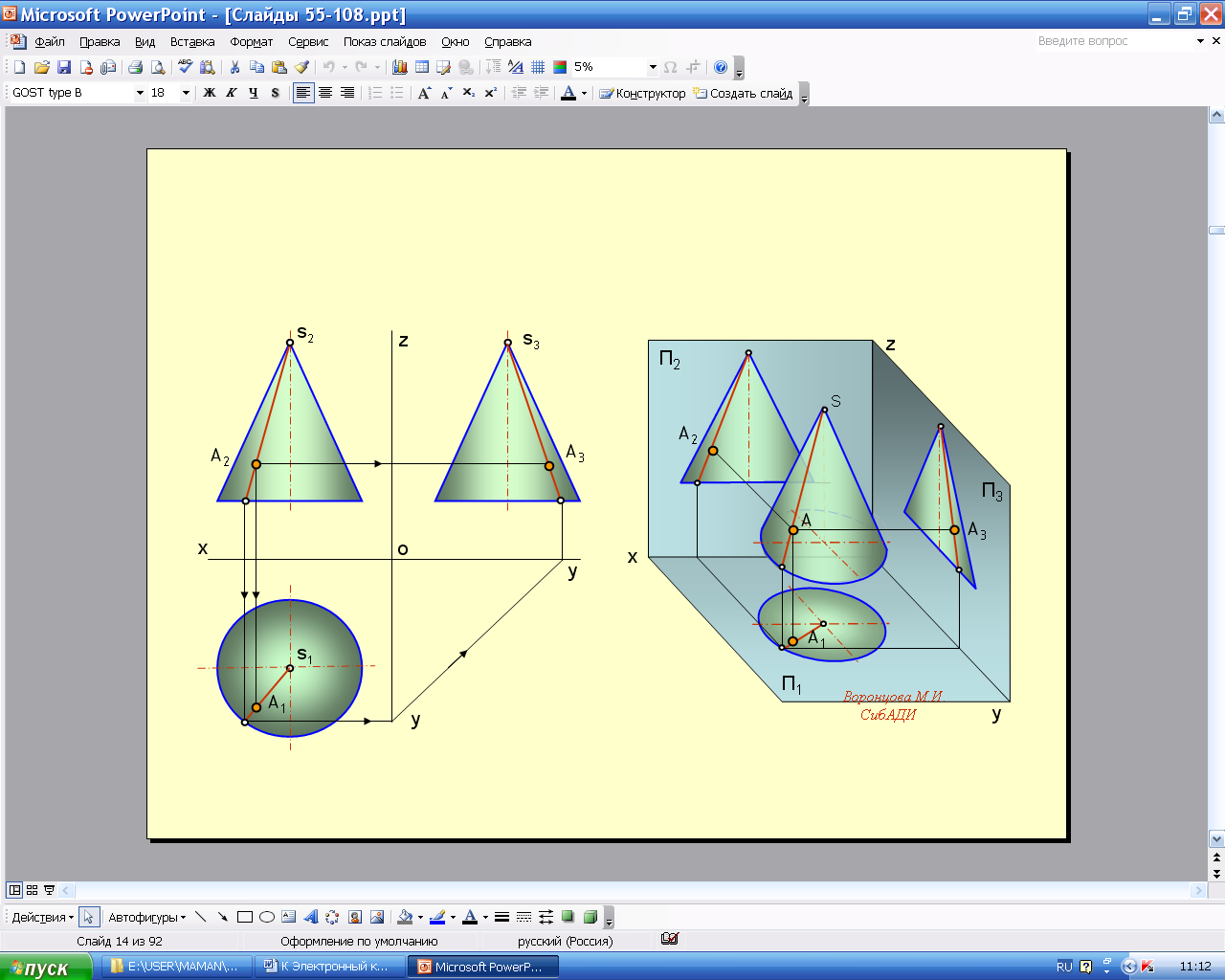
Анимации\Рис.5.68. Построение проекций точки на поверхности конуса.exe

3. Сфера образуется вращением окружности вокруг диаметра (рис. 5.69, а). На рис. 5.69, б изображен шар.

а б

Рис. 5. 69

4. Эллипсоид вращения образуется вращением эллипса вокруг одной из своих осей. При вращении вокруг большой оси образуется вытянутый эллипс (рис. 5.70, а), а при вращении вокруг малой оси образуется сжатый эллипс (рис. 5.70, б).

а б

Рис. 5.70. Эллипсоиды

5. Параболоид вращения образуется вращением параболы вокруг оси.

Параболоиды применяются в автомобильных фарах, антеннах (рис. 5.71).

Рис. 5.71. Параболические антенны

6. Тор образуется вращением окружности вокруг неподвижной оси, не проходящей через образующую окружность. Тор может быть открытым (рис. 5.72, 5.73, а, б, в), закрытым (рис. 5.72, 5.73, г, д, е), самопересекающимся (рис. 5.72, 5.73, ж, з, и).

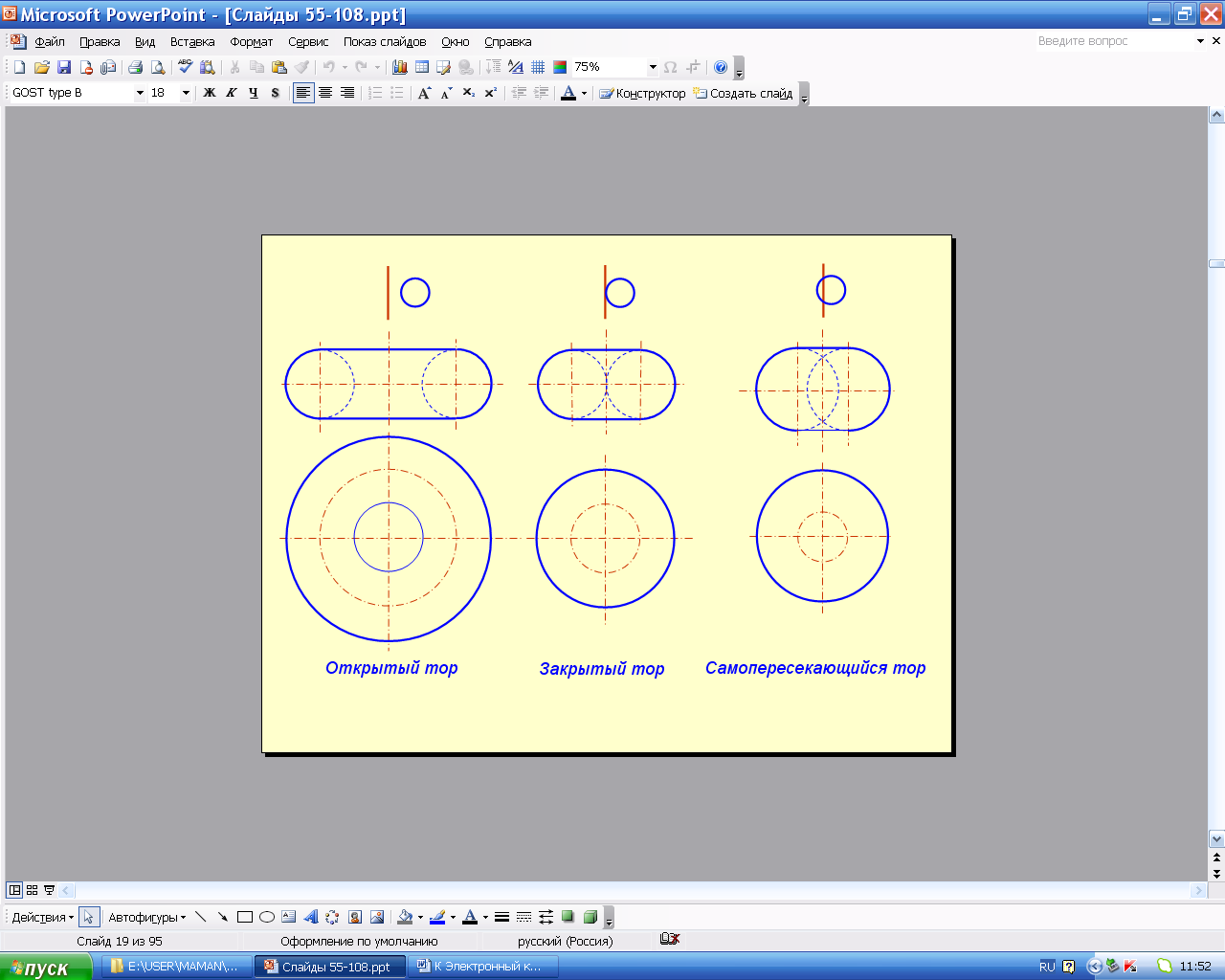
Рис.5.72. Разновидности тора

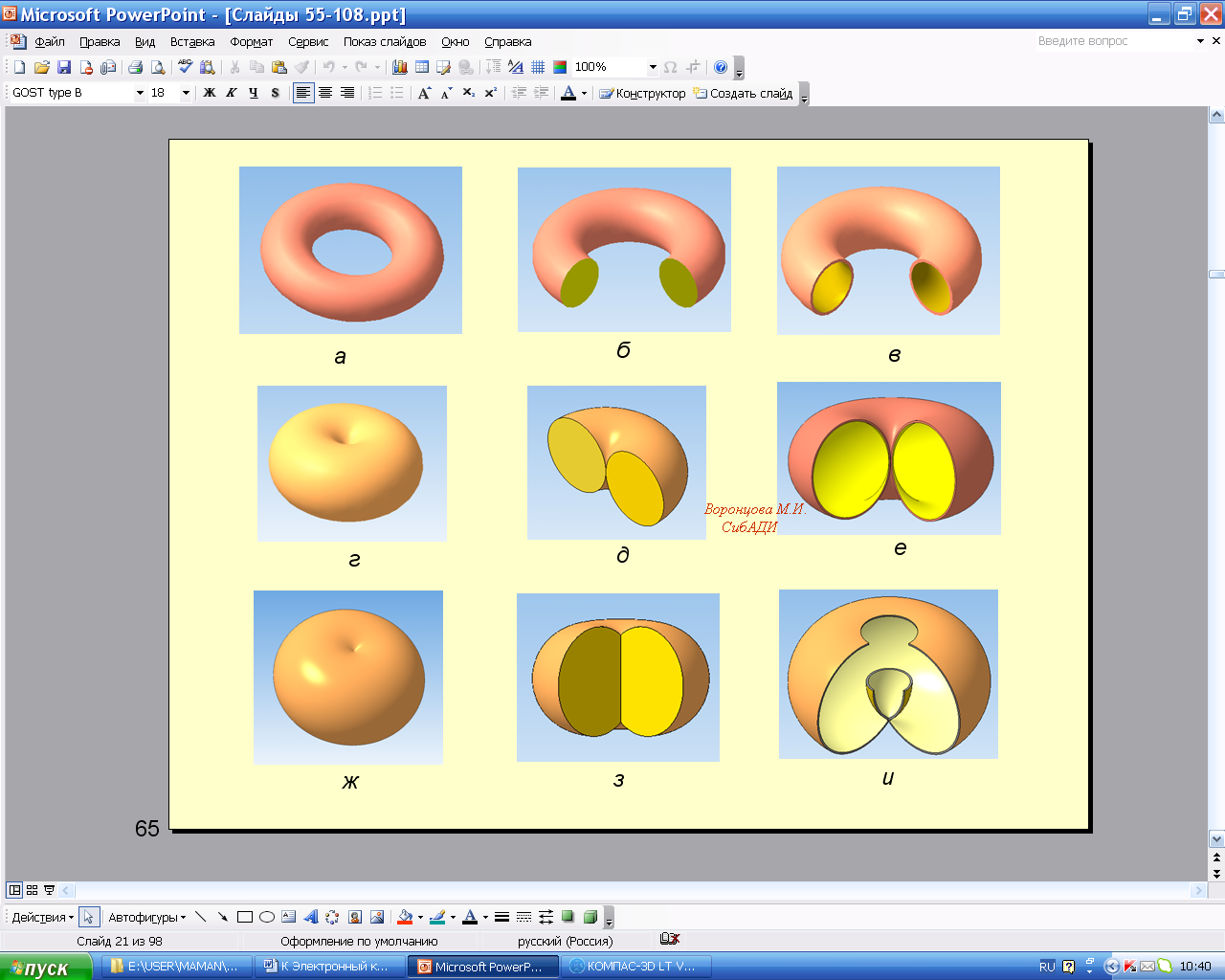
Рис. 5.73. Разновидности тора

На рис. 5.74, а изображен тор-бочка, а на рис.5.74, б – тор-глобоид.

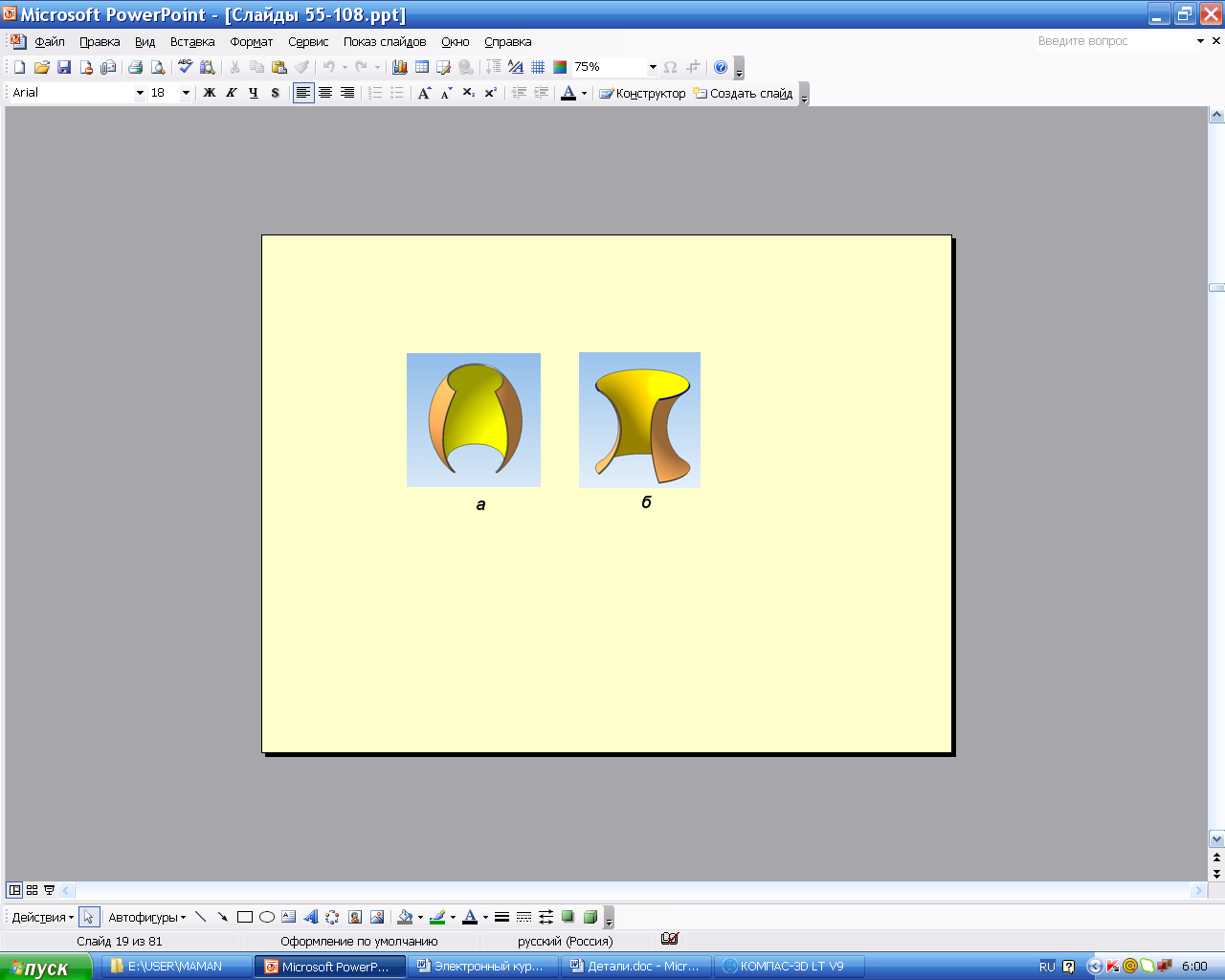
Рис. 5.74. Разновидности тора

7. Гиперболоид вращения образуется вращением гиперболы вокруг оси: двуполостный гиперболоид образуется при вращении гиперболы вокруг действительной оси (рис. 5.75), однополостный - при вращении вокруг мнимой оси. Однополостный гиперболоид рассматривают как линейчатую поверхность, образованную вращением одной из скрещивающихся прямых вокруг другой. Однополостные гиперболоиды применяют в строительной технике, сваривая легкие и прочные конструкции из труб. Примером такой конструкции является радиомачта на Шаболовке в Москве(6 гиперболоидов, установленных друг на друга).

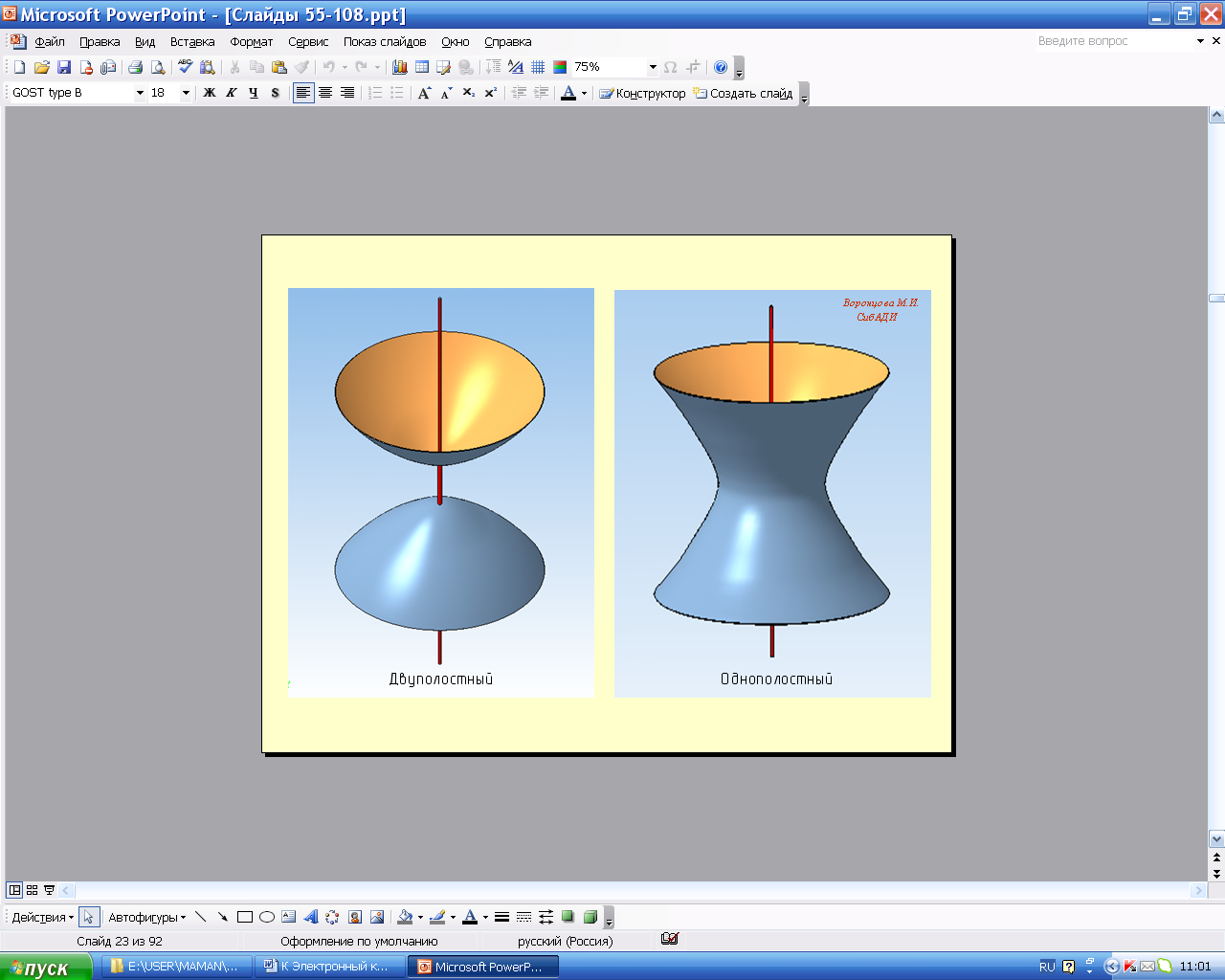
Рис. 5.75. Гиперболоиды