5 Функції робочого листа для роботи з матрицями

В MS Excel є функції робочого листа для роботи с матрицями, перераховані в таблиці 1.

При работі з матрицями, перед вводом формули, потрібно виділити область на робочому листі, куди буде занесений результат обчислень, а ввод формули завершати натисканням комбинації клавіш <Ctrl>+<Shift>+<Enter>.

Масиви в формулах можуть бути задані або як діапазон комірок, наприклад А1 : С3, або як масив констант, наприклад {1; 2; 3; 4; 5; 6; 7; 8; 9}, або як ім'я діапазона або масива.

Таблиця 1 – Функції обробки матриць

Функція (рос.)	Опис
МОБР(массив)	Повертає зворотню матрицю
МОПРЕД(массив)	Повертає розпізнавач матриці
МУМНОЖ (массив1;массив2)	Повертає матричний добуток двох матриць
ТРАНСП(массив)	Повертає транспоновану матрицю

6 Розв'язок системи лінійних рівнянь

Розв'яжемо як приклад систему лінійних рівнянь з двома невідомими, матриця коефіцієнтів якої записана в комірці А2:В3, а вільні члени — в комірці D2:D3 (рисунок 5).

Згадаємо, що розв'язання лінійної системи АХ = В, де А – матриця коефіцієнтів, В – стовпець (вектор) вільних членів, X – стовпець (вектор) невідомих, має вигляд X = А^-1В , де А^-1 – зворотна матриця к А. В нашому випадку

Тому, для розв'язання системи рівнянь

1. Виберіть той діапазон, в який буде введено розв'язок. Наприклад, F2:F3.

2. Введіть в нього формулу

=МУМНОЖ(МОБР(А2:ВЗ);D2:D3).

3. Завершіть введення формули натисканням комбінації клавіш <Ctrl>+<Shift>+<Enter>. MS Excel візьме формулу в рядку формул в фігурні дужки і відбудуться потрібні обчислення з елементами масиву (рисунок 36).

{=МУМНОЖ(МОБР(А2:ВЗ);D2:D3)}.

Рисунок 5 - Розв'язання системи лінійних рівнянь

Таким чином, розв'язанням системи рівнянь є вектор

Як більш складний приклад розв’яжемо систему лінійних рівнянь

А²Х= В,

де

Розв'язком цієї системи є вектор X = (А²)^-1 В. Для знаходження вектора X:

1. Введіть елементи матриці А в діапазон комірок А2:В3.

2. Введіть елементи вектора В в діапазон комірок D2:D3.

3. Виберіть діапазон F2:F3, куди помістимо елементи вектора розв'язання.

4. Введіть в цей діапазон формулу:

=МУМНОЖ (МОБР(МУМНОЖ(А2:В3;А2:ВЗ));D2:D3).

5. Завершіть введення формули натисканням комбінації клавіш <Ctrl>+<Shift>+ +<Enter>. MS Excel візьме формулу в рядку формул в фігурні дужки і відбудуться потрібні обчислення з елементами масиву.

{=МУМНОЖ (МОБР (МУМНОЖ (А2:ВЗ;А2:ВЗ));D2:D3)}.

В діапазоні комірок F2:F3 буде знайдено розв'язок системи рівнянь

7 Знаходження значення квадратичної форми

Розглянемо приклад обчислення квадратичної форми z = X^T АХ, при чому

Для знаходження значень цієї квадратичної форми:

1. Введіть елементи матриці А в діапазон комірок А2:B3 (рисунок 6).

2. Введіть елементи вектора X в діапазон комірок D2:D3.

3. Виберіть комірку G2, куди необхідно помістити значення квадратичної форми.

4. Введіть в цю комірку формулу

=МУМНОЖ(МУМНОЖ(ТРАНСП(D2:D3);А2:ВЗ);D2:D3)

5. Завершіть введення формули натисканням комбінації клавіш <Ctrl>+<Shift>+<Enter>. MS Excel візьме формулу в рядку формул в фігурні дужки і відбудуться потрібні обчислення з елементами масивів (рисунок 37).

(=МУМНОЖ(МУМНОЖ(ТРАНСП(D2:D3) ;А2:ВЗ) ;D2:D3)).

В комірці F2 буде знайдено питоме значення 196.

Хоча в даному прикладі формула повертає одно число, а не масив, тим паче, вона є формулою масиву. Тому не забудьте її введення завершити натисканням комбінації клавіш <Ctrl>+<Shift>+<Enter>. Якщо ви це не зробитте, в комірці F2 з'явиться повідомлення про помилку #знач !.

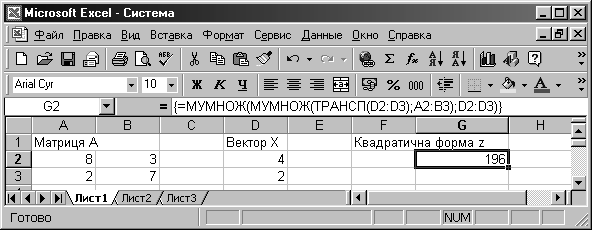
Рисунок 6 – Знаходження квадратичної форми