7.2. Исг на основе баллона

Ниже приводится схема источника сжатого газа (ИСГ) на основе баллона высокого давления. Схема ИСГ состоит из последовательного соединения баллона, электроклапана (ЭК), регулятора давления (РД) и привода. В баллоне газ находится под высоким давлением, которое падает по мере опорожнения баллона. Регулятор давления стабилизирует давление сжатого воздуха перед потребителем-приводом. Временная диаграмма изменений давлений в системе приводится ниже на графике.

График изменения давления при опорожнении баллона через регулятор давления. t_р - время работы привода.

На рисунках приведены возможные исполнения источника сжатого газа. Агрегат состоит из баллона 1(с разрезом) и воздушно-арматурного блока 2, в котором находится регулятор давления, зарядное устройство, пиропатрон включения.

Ниже показан другой пример исполнения воздушного баллона.

Одной из основных технических характеристик привода является максимальный расход привода G_z. Если задано время работы привода, то количество газа в ИСГ определяется простым соотношением

m_г = G_z*t_р.

На основании уравнения состояния pV = mRT несложно получить связь параметров газа и баллона с потребным количеством газа

Здесь V_б - объем баллона, р_бн и р_бк - начальное и конечное давления в баллоне. Соотношение получено при постоянстве температуры газа в баллоне, т.е при изотермическом процессе. При адиабатическом процессе опорожнения баллона связь массы газа с объемом будет

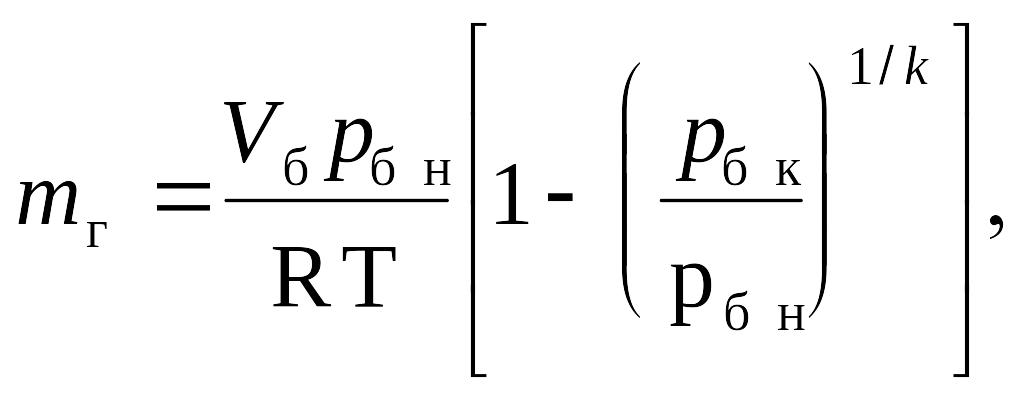
где k - показатель адиабаты.

Приведенные соотношения показывают, что при адиабатическом опорожнении из баллона при одинаковых начальном и конечном давлении можно изъять меньшее массовое количество газа. Адибатическое расширение характерно для достаточно теплоизолированного баллона при быстром опорожнении. Давление в баллоне выбирается достаточно часто в диапазоне 30…40 МПа, давление на входе в привод находится в диапазоне 1,5 … 2,5 МПа.

Конечное давление исходя из обеспечения работы регулятора давления выбирается равным

p_бк = p_z/b_k._.

Пример.

Рассмотрим некоторые расчетные результаты для опорожнения гипотетического баллона со сжатым воздухом.

Исходные данные:

Параметр	Воздух	Гелий	Размерность
Объем баллона Vб =	0,001	0,001	м3
Отношение теплоемкостей k=	1,4	1,66	-
Газовая постоянная R=	286,7	2087	Нм/(кгК)
Начальная температура Тнач =	293	293	К
Начальное давление в баллоне рбн =	30	30	МПа
Конечное давление в баллоне рбк =	1	1	МПа

1. При изотермическом процессе опорожнения баллона от р_бн до р_бк получим массовое количество, отдаваемого газа в систему

Воздух:

m_г = (V_б/RT)*(p_бн – p_бк) = 0,001*(30 – 1)*10⁶/(286,7*293) = 0,345 кг.

Гелий:

m_г = (V_б/RT)*(p_бн – p_бк) = 0,001*(30 – 1)*10⁶/(2087*293) = 0,047 кг.

2. При адиабатическом процессе опорожнения баллона от р_бн до р_бк получим массовое количество, отдаваемого газа в систему

Воздух:

m_г = (V_б/RT)* p_бн*(1 – (р_бк/ р_бн )^1/k) = 0,001*30*10⁶*0,912/(286,7*293) = 0,326 кг.

Гелий:

m_г = (V_б/RT)* p_бн*(1 – (р_бк/ р_бн )^1/k) = 0,001*30*10⁶*0,912/(2087*293) = 0,045 кг.

Из расчетов видно, что при адиабатическом процессе опорожнения баллона отбирается меньшее количество газа, а так же и при увеличении газовой постоянной.

3. Рассмотрим изменение давления в баллоне при изменении температуры на ±60⁰. Закачиваем баллон при Т_нач = 293 К до давления р_бн = 30 МПа, тогда при:

- повышении температуры на 60⁰ , Т= 273 + 60 = 333К получаем

р_бн = 30*333/293 = 34,1 МПа,

- понижении температуры на 60⁰, Т = 273 – 60 = 213К , получим

р_бн = 30*213/293 = 21,8 МПа.

Первое давление (34,1 МПа) необходимо закладывать в расет прочности баллона, второе давление (21,8 МПа) будет определять время работы системы. Это подтверждается следующими соображениями. Если баллон заправить сжатым воздухом до давления р_бн = 30 МПа при температуре 293К, а затем охладить до температуры 213К, то теперь начальное давление станет р_бн = 21,8 МПа и при опорожнении баллона от этого начального давления до требуемого конечного давления сможем получить при этом только 0,248 кг газа, а если иметь в виду, что при этом увеличится расход привода, то этот режим должен быть обязательно учтен при проектировании.

Рассматривая шаровой баллон как тонкостенный сосуд, находящийся под действием внутреннего даления р_б, в первом приближении можно для толщины стенок h записать следующее выражение

h = k₃r_вн/(2σ),

где k_{3 –} коэффициент запаса (≈2)_, r_вн – внутренний радиус баллона, σ – предел прочности материала баллона. Внутренний радиус шарового баллона определяется соотношением

Полная масса источника сжатого газа m_исг естественно равна сумме массы газа и массы баллона

m_исг=m_r[1+(( ρ_мRT*F(p_б))/σ)],

здесь ρ_м - плотность материала баллона, R – удельная газовая постоянная,T – температура газа в баллоне .

Функция F(p_б) определяется давлением в баллоне p_б, запасом прочности k₃ ,пределом прочности σ и при изменении давления p_б в диапазоне от 0 до 50 МПа, а предела прочности σ от 400 до 1000 МПа изменяется на 10%.

Приведенное выражение для массы ИСГ показывает, что она пропорциональна потребной массе газа, кроме того для баллона желательно применять материал с малой плотностью и большим пределом прочности, а также что предпочтительным является газ с меньшей газовой постоянной. В данном случае масса ИСГ составляет 1,5…3,0 потребной массы сжатого газа.

Нужно заметить, что меньшее количество газа в баллоне компенсируется меньшим потребляемым расходом газа

G_z = mA_1mp_zФ(k)Ф(RT), -------

так как в выражение для расхода входит функция Ф(RT) = √1/(RT) , то

соотношение времени работы автономной системы на воздухе t_рв и на время работы на гелии t_рг будут связаны соотношением квадратных корней из удельных газоваых постоянных

t_рг = t_рв (√R_в/√ R_г).