3.4. Течение газа по каналам переменного сечения.

Рассмотрим течение газа по каналам переменного сечения. Поток газа является неразрывным

G = Aw/v, Gv = Aw.

Продиффиринцируем это уравнение

при G = const

Adw + wdA = Gdv

и разделим на исходное

Полученное выражение называется уравнением неразрывности газового потока в дифференциальной форме.

Рассмотрим это выражение для адиабатического потока (pv^k = const)

v^kdp + kp v ^k-1dv = 0

и разделив полученное на исходное

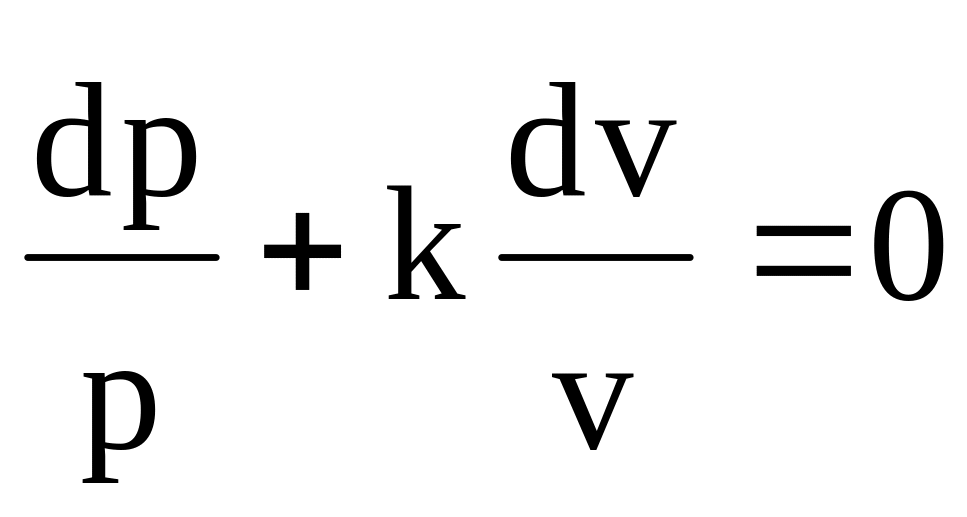
или

На основании первого закона термодинамики для теплоизолированного потока

d(w²/2) = - vdp

wdw= -vdp.

Разделим последнее на квадрат скорости

Подставим полученные выражения в уравнение неразрывности газового потока в дифференциальной форме.

в полученном выражении k>0, p>0, w²>0. Следовательно числитель дроби будет определять соотношение знаков полученного уравнения.

Полученное уравнение связывает знак изменения площади dA потока с изменением давления dp и скорости w. Рассмотрим полученные результаты.

1. Рассмотрим течение газа в соплах. Соплом называется устройство, в котором газ расширяется при этом давление его падает (dp < 0). Как будет вести себя газовый поток при различной начальной скорости. При этом следует учитывать закономерность, вытекающую из первого закона термодинамики: знак приращения скорости противоположен знаку приращения давления в потоке.

1.1. Дозвуковое течение a²-w² >0, по определению приращение давления отрицательно, следовательно изменение площади должно быть отрицательным, т.е. канал сужается dA < 0. Напомним общее правило - в потоке знаки приращения скорости и давления противоположны.

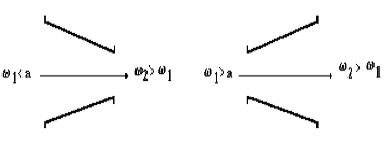
1.2. Сверхзвуковое течение

a²-w² <0, канал расширяется dA > 0. В обоих случаях происходит разгон потока.

2. Рассмотрим течение газа в диффузорах. Диффузором называется устройство, в котором газ сжимается при этом давление его растет (dp > 0). Как будет вести себя газовый поток при различной начальной скорости:

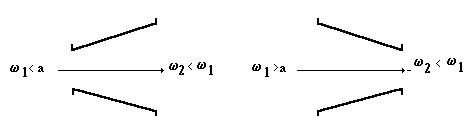1.1. Дозвуковое течение

a²-w² >0, канал расширяется dA > 0

2.2. Сверхзвуковое течение

a²-w² <0, канал сужается dA > 0. В обоих случаях поток тормозится.

Из проведенного анализа следует, что в зависимости от скорости потока на входе в канал переменного сечения возможно его торможение или разгон, что определяется конфигурацией канала.

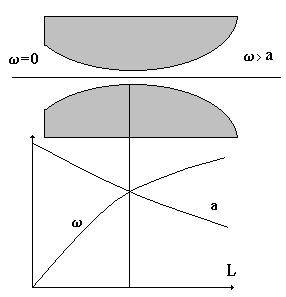
3.5. Сопло Лаваля.

В технических устройствах часто возникает необходимость превращения потенциальной энергии давления газа в кинетическую энергию движущегося потока. Для этого необходимо разогнать газ до максимальной скорости. Максимальный разгон газа будет при его расширении до окружающего давления. Устройством, обеспечивающим данный процесс является сопло Лвавля, предложенное Карлом Густавом Патриком де Лавалем (1845-1913) шведским инженером специалистом по паровым турбинам.

Лаваль (Laval) Карл Густав Патрик де (9.5.1845, Орса, ≈ 2.2.1913, Стокгольм), шведский инженер и изобретатель. По национальности француз. Окончил технологический институт и университет (1872) в Упсале. В 1878 сконструировал центробежный сепаратор непрерывного действия (для молока). В 1889 построил паровую турбину активного типа. Впервые применил расширяющиеся сопла, гибкий вал, диск равного сопротивления, позволивший достигать очень высоких окружных скоростей (419 м/сек). Кроме того, в турбинах Л. были предусмотрены многие новые элементы, часть из которых используется в современном турбостроении. Л. разработал также теорию сопла. Вследствие ряда конструктивных недостатков и относительно небольшой мощности турбины Л. не получили распространения, но сыграли важную роль в развитии турбостроения.Он соединил два сопла, обеспечивая разгон газа от нулевой скорости до сверхзвуковой, при этом газ расширялся до окружающего давления.

В критическом сечении сопла устанавливается скорость потока, равная скорости звука

Пример.

В качестве примера проведем оценку параметров воздушного течения. В прессе сообщалось, что вокруг земли имеется воздушная река. Река зарождается в Северной Америке (предположительно из-за торнадо), пересекает Атлантический океан, Гималаи, Японию, Тихий океан, еще раз Северную Америку и пропадает в районе Британских островов. Река течет на высоте 7 - 9 километров со скоростью 300 - 400 км/час. Ширина реки 100 - 200 км. Течет она уже давно.

Рассмотрим расход сжатого воздуха в этой реке.

Исходные данные для расчета примем следующие

Сечение потока А = 100 км*2км = 2*10⁸ м²,

Скорость потока v = 400 км/час = 111 м/сек,

Давалние в потоке на этой высоте около p = 0,03 МПа,

Температура в потоке T = 230 K

Удельная газовая постоянная R =286,7 Дж/кгК

Плотность воздуха определяется из уравнения состояния

 = 0,03*10⁶/(286,7*230) = 0,455 кг/м³.

Расход воздуха в реке через принятое сечение будет

G = Av

G = 2*10⁸*111* 0,455  1*10¹⁰ кг/сек.

Мы получили колосальное количества газа пролетающее через сечение в одну секунду, но это ничтожно по сравнению с массой атмосферы земли (Масса атмосферы земли составляет 5,15*10¹⁸ кг). Для полного перемещения массы воздуха атмосферы этой рекой потребуется около 1000 лет.

Если повернуть этот поток по радиусу от земл, то мы будеи иметь реактивный даигатель, оценка тяги которого будет

F = G*v.

F = 10¹⁰* 111 10¹³ Ньютонов.

при тяге баллистической ракеты порядка 3*10⁹ Ньютона (10000 ракет). (10⁶Н)

Масса земли составляет 5976*10²¹ кг.