2.6. Термодинамические процессы.

Первый закон термодинамики устанавливает связь между подведенной теплотой, внутренней энергией и работой. Уравнеие состояния определяет связь между параметрами ТРТ. Рассмотрим, что происходит с ТРТ при подводе теплоты. Очевидно предположить, что параметры изменятся. Раньше говорилось, что это изменение состояния ТРТ назвается процессом. Преобразование теплоты в работу и внутреннюю энергию зависит от вида процесса.

Ряд процессов имеет аналитическое описание:

- изохорный, при v = const,

- изобарный, при p = const,

- изотермический, при T = const,

- адиабатический, при отсутствии теплообмена q =0,

- политропный, при постоянной теплоемкости c_п = const.

Практические случаи описания работы различных элементов пневмоавтоматики и пневмопривода удается подвести под тот или иной процесс и получить необходимые проектные выводы.

Анализ термодинамических процессов обычно проводится по одному шаблону:

- определяем кривую процесса на pv-диаграмме,

- определяем связь между основными параметрами состояния p₁,v₁,T₁ и р₂,v₂,T₂,

- определяем изменение внутренней энергии системы,

- определяем работу процесса,

- определяем изменение энтальпии,

- определяем изменение энтропии (в данном курсе понятие энтропии не рассматривается, т.к. оно необходимо, в основном, для проверки гипотез – настоящий курс прикладной и посвящен рассмотрению провереных гипотез описания процессов в элементах пневмоавтоматики). (Энтропия не убывает).

Будем считать газ идеальным.

2.6.1. Изохорный процесс.

В этом процессе v = const, следовательно dv = 0.

Из уравнения состояния получим

p/T = R/v = const,

откуда

Графически в координатах p-v процесс изображается вертикальной прямой.

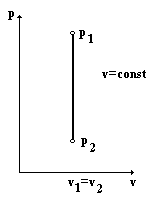
Из первого закона термодинамики следует

dq = du = c_v dT, так как dv =0.

В этом процессе вся теплота идет на изменение внутренней энергии системы.

Энтальпия системы определяется i = c_p dT.

2.6.2. Изобарный процесс.

В этом процессе p = const, следовательно dp = 0.

Из уравнения состояния получим

v/T = R/p = const,

откуда

это соотношение называется законом Гей-Люссака.

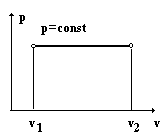
Из первого закона термодинамики следует

dq = di = c_pdT, так как dp =0.

В этом процессе вся теплота идет на изменение энтальпии системы.

Энтальпия системы определяется

i = c_p dT.

Внутренняя энергия системы

u = c_v dT.

Работа газа в процессе

l = pdv = p(v₂ - v₁).

2.6.3. Изотермический процесс.

В этом процессе T = const, следовательно dT = 0.

Из уравнения состояния получим

pv = RT = const,

откуда

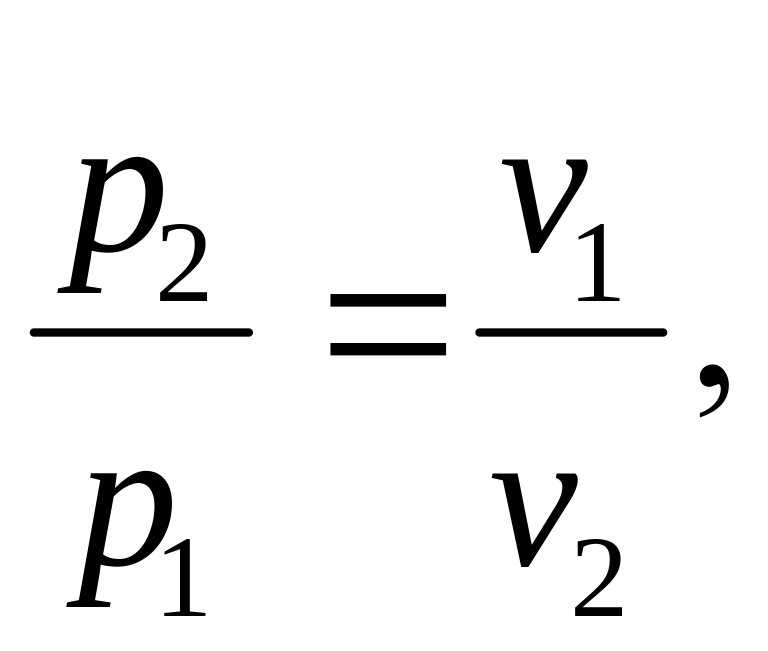
(Закон Бойля-Мариотта).

Так как внутренняя энергия и энтальпия определяются изменением температуры

du = c_v dT = 0, di = c_pdT = 0,

то они в этом процессе неизменны.

Из первого закона термодинамики получаем

dq = c_v dT + pdv = pdv = dl.

В этом процессе вся теплота идет на совершение работы системой.

Для определения работы процесса нужно проинтегрировать приращение работы при условии p = RT/v

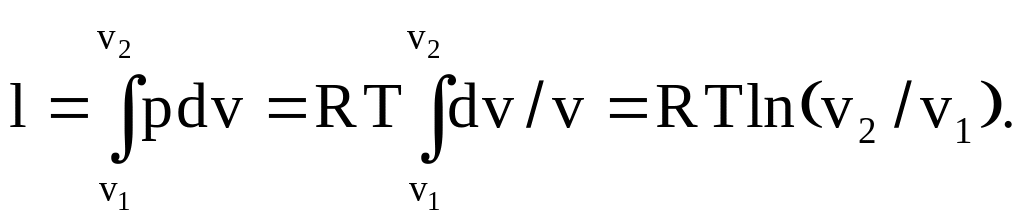
Следует отметить, что работа процесса зависит от начальных условий (T).

Так как теплоемкость есть c = dq/dT , а dT = 0, то теплоемкость этого процеса равна бесконечности. Ниже приведен график изменения параметров в процессе.