4.1. Передача теплоты через плоскую стенку.
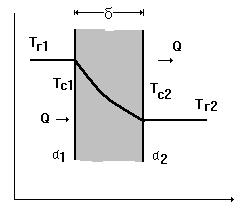
Рассмотрим передачу теплоты через плоскую бесконечную стенку в предположении установившегося режима. Схема передачи теплоты приводится ниже
Задано: Тг1 - температура газа слева от стенки, Tг2 - температура газа справа от стенки, Tc1 - температура стенки слева, Tc2 - температура стенки справа, a1 - теплопроводность стенки слева, a2 - теплопроводность стенки справа, Q теплота подведенная к стенке, l - теплопроводность материала стенки, d - толщина стенки.
Необходимо определить: коэффициент теплопередачи стенки.
Рассмотрим последовательно процесс передачи теплоты через плоскую стенку. Процесс передачи теплоты от газа к стенке описывается уравнением Ньютона-Рихмана
Q = a1A(Tг1 - Tс1).
Процесс передачи теплоты по материалу стенки на основании уравнения Фурье после интегрирования будет (стенка принята плоской и бесконечной, для упрощения интегрирования уравнения Фурье)
Q = (l/d)A(Tc1 - Tc2).
Процесс передачи теплоты от стенки к газу описывается уравнением Ньютона-Рихмана
Q = a2A(Tс2 - Tг2).
Разрешим приведенные уравнения относительно температуры
Tг1 - Tс1= Q/( a1A)
Tc1 - Tc2= Q/(A(l/d))
Tс2 - Tг2= Q/(a2A).
После суммирования уравнений получим
откуда можно записать
Q = kтA(Tг1 - Tг2),
где
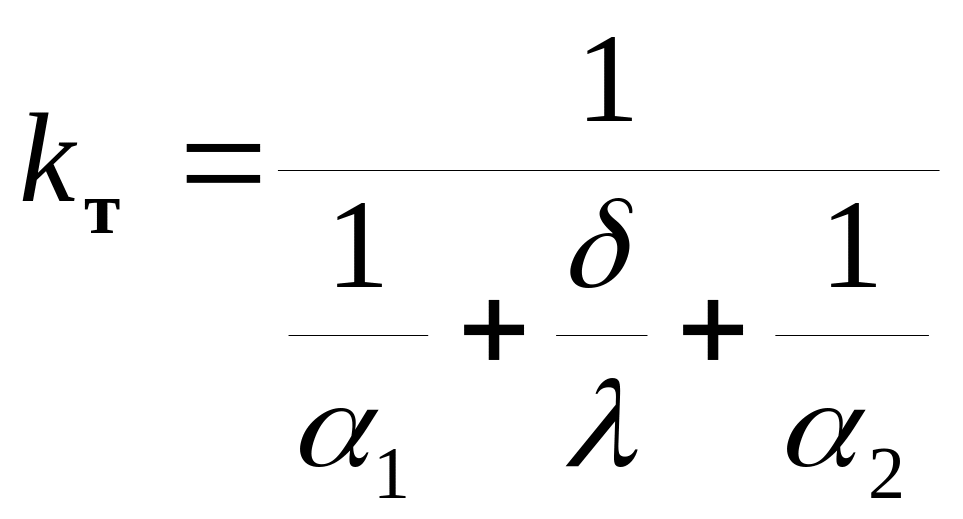
kт - коэффициент теплопроводности стенки в данных условиях. Выражение для коэффициента и его составляющие ясны из приведенных выкладок.