Не согласен 1 2 3 4 5 6 7 Согласен

Оценки степени согласия с утверждением о допустимости телесных наказаний после предъявления видеозаписи / текста приведены в таблице.

С помощью методов описательной статистики выполнить сравнительный анализ результатов двух разных способов воздействия на испытуемых.

№	Экспериментальная группа	Контрольная группа
1	4	4
2	1	7
3	5	2
4	5	3
5	3	5
6	5	1
7	3	5
8	6	2
9	7	4
10	3	5
11	6	5
12	5	2
13	7	1
14	6	3
15	6	4
16	7	4
17		3
18		6

Теоретические сведения

Меры центральной тенденции

К характеристикам положения относятся следующие оценки центральной тенденции: мода (Мо), медиана (Ме) и среднее арифметическое (M).

Важное значение имеет такая величина признака, которая встречается чаще всего в изучаемом ряду, в совокупности. Такая величина называется модой (Мо).

При расчете моды может возникнуть несколько ситуаций:

1. Два значения признака, стоящие рядом, встречаются одинаково часто. В этом случае мода равна среднему арифметическому этих двух значений.

2. Два значения, встречаются также одинаково часто, но не стоят рядом. В этом случае говорят, что ряд данных имеет две моды, т.е. он бимодальный.

3. Если все значения данных встречаются одинаково часто, то говорят, что ряд не имеет моды.

Чаще всего встречаются ряды данных с одним модальным значением признака. Если в ряду данных встречается два или более равных значений признака, то говорят о неоднородности совокупности.

Вторая числовая характеристика ряда данных называется медианой (Ме) – это такое значение признака, которое делит ряд пополам. Иначе, медиана обладает тем свойством, что половина всех выборочных значений признака меньше её, половина больше. При нечетном числе элементов в ряду данных, медиана равна центральному члену ряда, а при четном среднему арифметическому двух центральных значений ряда.

Вычисление медианы имеет смысл только для порядкового признака.

Среднее арифметическое значение признака вычисляется по формуле (1):

(1)

где x_i – значения признака, n – количество данных в рассматриваемом ряду.

Среднее арифметическое значение признака, вычисленное для какой-либо группы, интерпретируется как значение наиболее типичного для этой группы человека. Однако бывают случаи, когда подобная интерпретация несостоятельна (в случае, если существует большая разница между минимальным и максимальным значениями признака).

Меры изменчивости

Используя для описания ряда значений признака, только меру центральной тенденции, можно сильно ошибиться в оценке характера изучаемой совокупности. Это хорошо видно на следующем примере. Допустим, мы изучаем средний возраст в двух группах, состоящих каждая из 6-ти человек. Значения признака распределились следующим образом:

1 группа – 10, 10, 10, 50, 50, 50

2 группа – 30, 30, 30, 30, 30, 30

Подсчитав среднее значение в каждой из групп, получим М₁= 30 и М₂=30. Т.е. мы получили одинаковые значения, тогда как совершенно очевидно, что выборки взяты из разных совокупностей. Ошибка произошла из-за разброса значений возраста в этих группах.

Существует несколько способов оценки степени разброса или рассеивания данных. Основными характеристиками рассеивания являются: размах (R), дисперсия (D), среднеквадратическое (стандартное) отклонение (σ – сигма), коэффициент вариации (V).

Простейший из параметров распределения, размах – это разность между максимальным и минимальным значениями признака: R = x_max – x_min.

Дисперсия показывает разброс значений признака относительно своего среднего арифметического значения, то есть насколько плотно значения признака группируются вокруг M; чем больше разброс, тем сильнее варьируются результаты испытуемых в данной группе, тем больше индивидуальные различия между испытуемыми:

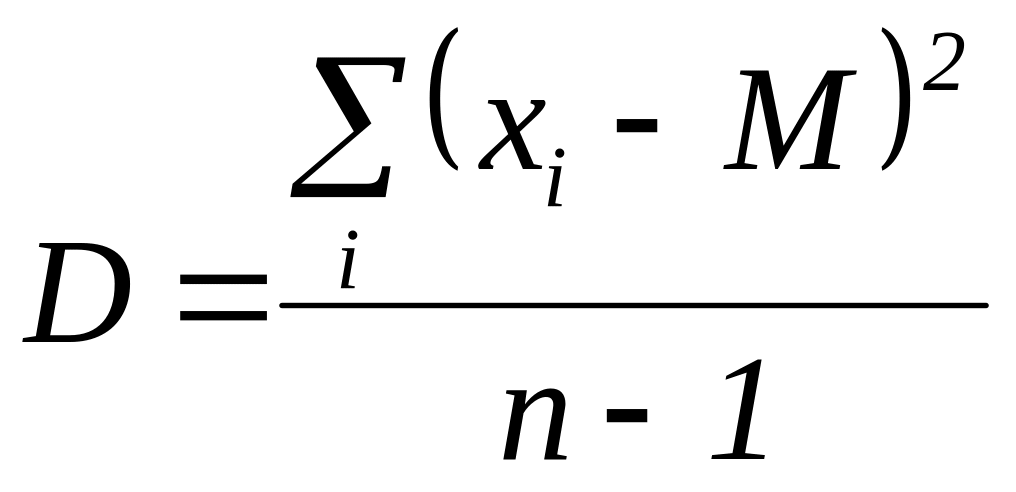(2)

где x_i – значения признака, M – среднее значение признака, n – количество данных в рассматриваемом ряду.

Из формулы видно, что дисперсия имеет "квадратный размер": если величина измерена в баллах, то дисперсия характеризует ее разброс в "баллах в квадрате", и т.п. Большую наглядность в отношении разброса имеет среднеквадратическое отклонение (стандартное отклонение), так как его размерность соответствует размерности измеряемой величины:

(3)

где D – дисперсия выборки

Коэффициент вариации вообще не имеет размерности, что позволяет сравнивать вариативность случайных величин, имеющих различную природу:

(4)

где σ – стандартное отклонение выборки, M – среднее значение признака.

Алгоритм расчета эмпирических и теоретических частот

1. Данные сортируются по убыванию.

2. Подсчитывается частота повторения каждого значения – это и есть эмпирическая частота (m). Вычисляется относительная частота по формуле .

3. Вычисляется среднее ряда (М).

4. Вычисляется стандартное отклонение (σ).

5. Находится теоретическая относительная частота с помощью функции NORMDIST

6. Вычисление эмпирических асимметрии (SKEW) и эксцесса (KURT).

Асимметрия – это показатель симметричности/скошенности кривой распределения, а эксцесс определяет ее островершинность. При левосторонней асимметрии ее показатель является положительным значения признака. При правосторонней – показатель отрицательный и преобладают более высокие значения. У всех симметричных распределений (в том числе и у нормального распределения) значение асимметрии равно нулю. Если в распределении преобладают значения близкие к среднему арифметическому, то формируется островершинное распределение. В этом случае показатель эксцесса стремится к положительной величине. У нормального распределения эксцесс равен нулю. Если у распределения две вершины (бимодальное распределение), то его эксцесс стремится к отрицательной величине.

7. Вычисление критических значений асимметрии и эксцесса по формулам:

Распределение считается нормальным, если эмпирический результат абсолютной величины показателей асимметрии и эксцесса превышает их критические значения или равен им. Критические значения вычисляются по следующим формулам:

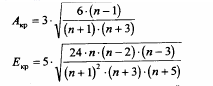
Пример 1

У студентов первого и второго курса был исследован уровень самооценки. Сделать сравнительный анализ, используя методы описательной статистики. Результаты тестирования приведены в таблице.

№	Группа 1	Группа 2
1	0,12	0,54
2	0,47	0,43
3	0,38	0,56
4	0,23	0,35
5	0,19	0,98
6	0,63	0,73
7	0,56	0,35
8	0,55	0,96
9	0,58	0,75
10	0,45	0,34
11	0,35	0,35
12	0,73	0,53
13	0,21	0,36
14	0,35

1. Вычислим медиану с помощью функции MEDIAN.

2. Вычислим медиану с помощью функции MODE.

3. Вычислим с помощью функции AVERAGE среднее выборок.

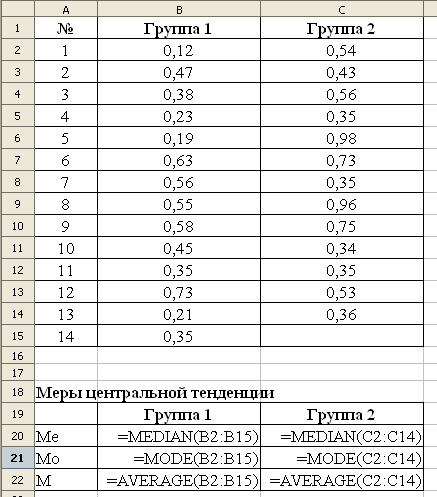
В результате расчетов получены значения

Показатель	Группа 1	Группа 2
Ме	0,42	0,53
Мо	0,35	0,35
М	0,41	0,56

Медиана и среднее в группе 2 выше, чем в группе 1, что свидетельствует о том, что уровень самооценки в группе 2 значительно выше. Моды признаков в обеих группах абсолютно одинаковые.

4. Вычислим дисперсию с помощью функции VAR.

5. Вычислим стандартное отклонение с помощью функции STDEV.

6. Вычислим с помощью формулы =(F21/B22)*100 коэффициент вариации для группы 1 и скопируем формулу с помощью маркера заполнения.

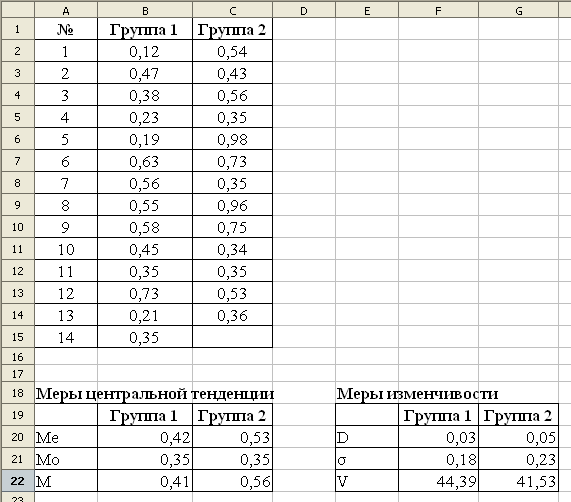
Поскольку показатели разброса данных (дисперсия и стандартное отклонение) меньше для показателей группы 1, то это свидетельствует о том, что первая выборка более однородная.

Показатель	Группа 1	Группа 2
D	0,03	0,05
σ	0,16	0,23
V	44,39	41,53

Пример 2

В группе из 30 добровольцев-студентов, был проделан опыт по изучению глазодвигательной координации. Задача заключалась в том, чтобы поражать предъявляемые на дисплее движущиеся мишени. Были предъявлены 10 последовательностей из 25 мишеней. Построить кривую распределения величины, отражающей количество пораженных мишеней.

Вычисление эмпирических частот (в ячейке Е2) осуществляется с помощью функции =COUNTIF($B$2:$B$16;D2) дальше протянуть.

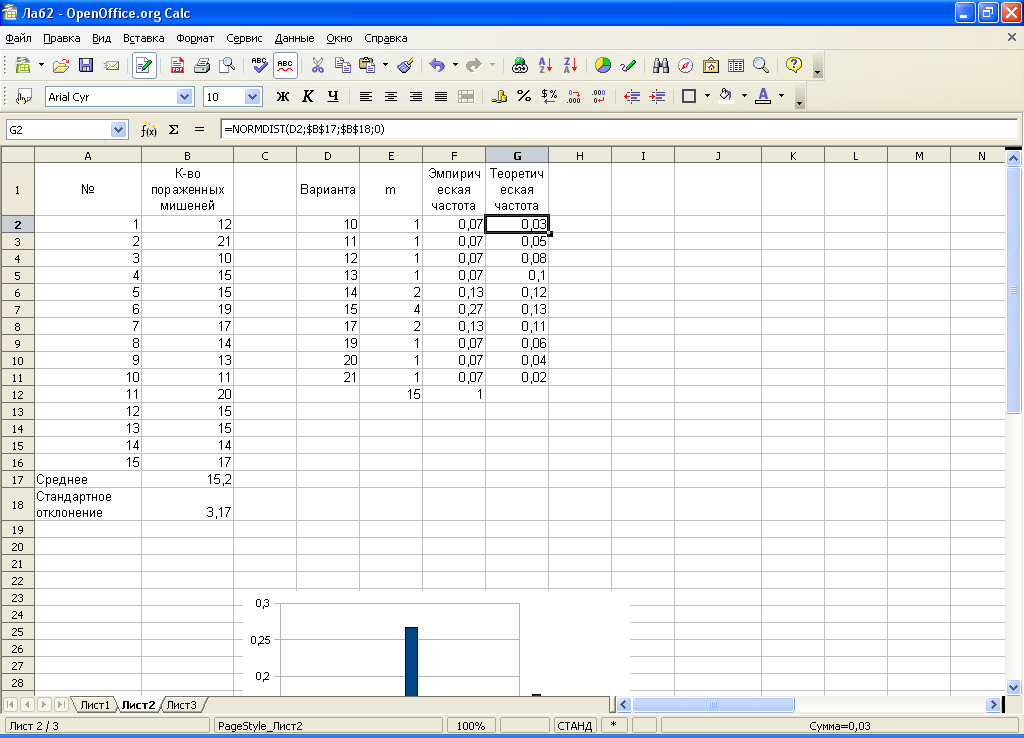
Построен график и гистограмма распределений:

Значения асимметрии и эксцесса на основании наблюдаемых значений, вычислены с помощью статистических функций =SKEW(B2:B16) и =KURT(B2:B16) и равны соответственно: , . Критические значения в соответствии с формулами вычисляются:

=3*SQRT(6*(A16-1)/((A16+1)*(A16+3)))

=5*SQRT((24*A16*(A16-2)*(A16-3))/(((A16+1)^2)*(A16+3)*(A16+5)))

	Эмпирические	Критические
Асимметрия	0,29	1,62
Эксцесс	-0,42	3,9

и , т.е. эмпирические значения А и Е меньше критических значений. Можно сделать следующий вывод: распределение результативного признака в данном примере не отличается от нормального распределения.