Фінансові ренти

Потік платежів, усі члени якого позитивні величини, а часові інтервали між двома послідовними платежами постійні, називають фінансовою рентою, або ануїтетом.

Нарощена сума річної звичайної постійної ренти:

,

де — коефіцієнт нарощення ренти, значення якого подаються в додатках.

Річна рента, нарахування відсотків m разів на рік. Це випадок, коли відсотки нараховуються m разів на рік на платежі, які вносяться один раз на рік, а відсотки нараховуються за ставкою j/m. Нарощена сума членів цієї зростаючої скінченої геометричної прогресії дорівнюватиме:

.

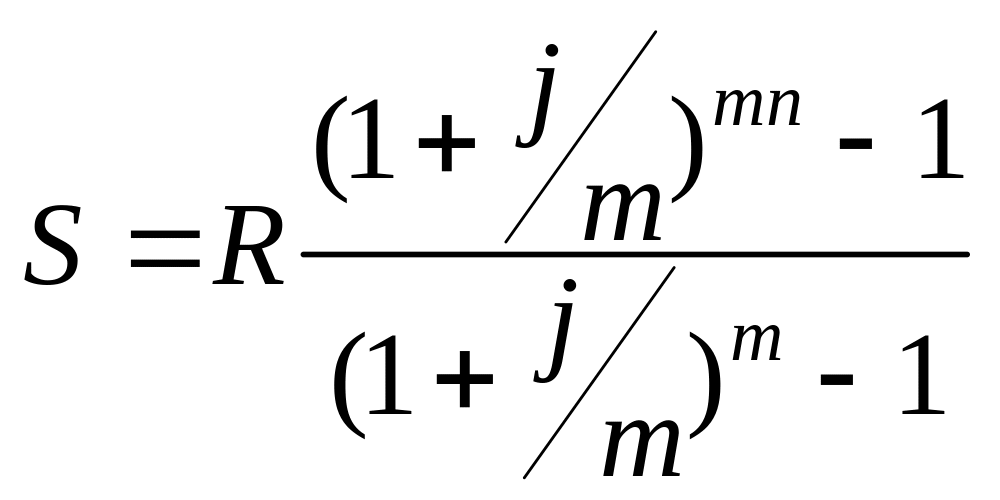Рента р-термінова (m=1). Визначимо нарощену суму за умови, що рента виплачується р разів на рік рівними платежами R/p, а відсоток нараховується один раз наприкінці року:

.

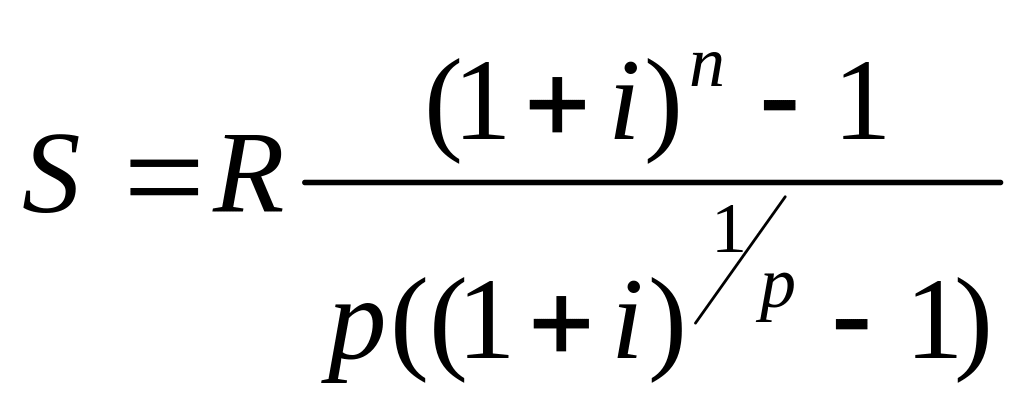Ренти р-термінові (p = m). Число членів ренти на рік дорівнює числу нарахувань відсотків протягом року p = m:

.

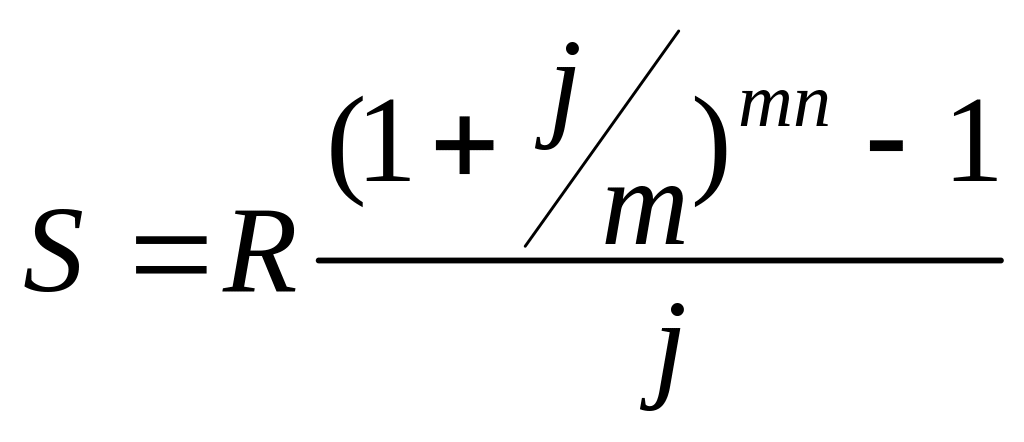Рента р-термінова . Загальний випадок р-термінової ренти з нарахуванням відсотків m разів на рік:

.

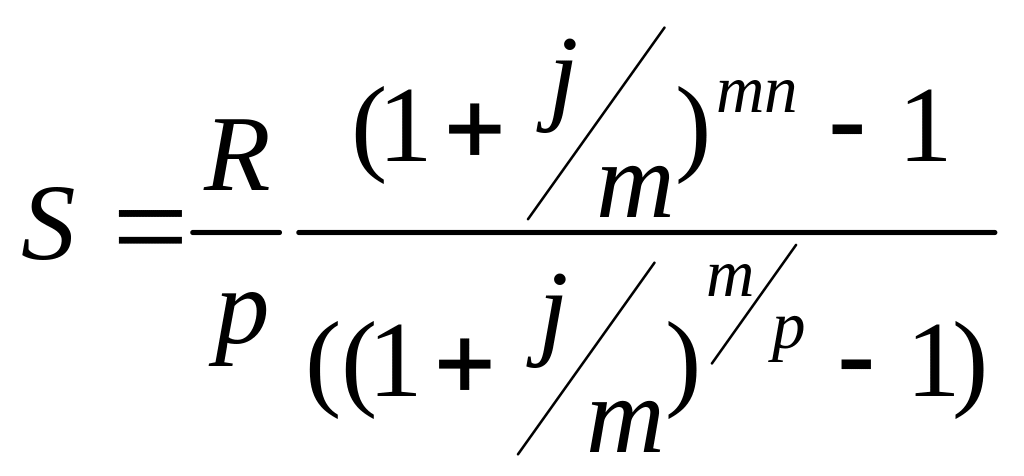Сучасна величина річної ренти визначається як сума геометричної прогресії за такою формулою:

,

де А — сучасна величина ренти; a_n;i — коефіцієнт приведення ренти. Цей коефіцієнт показує, у скільки разів сучасна величина більша за її член.

Графічно сучасну величину ренти можна представити таким чином (рис 1):

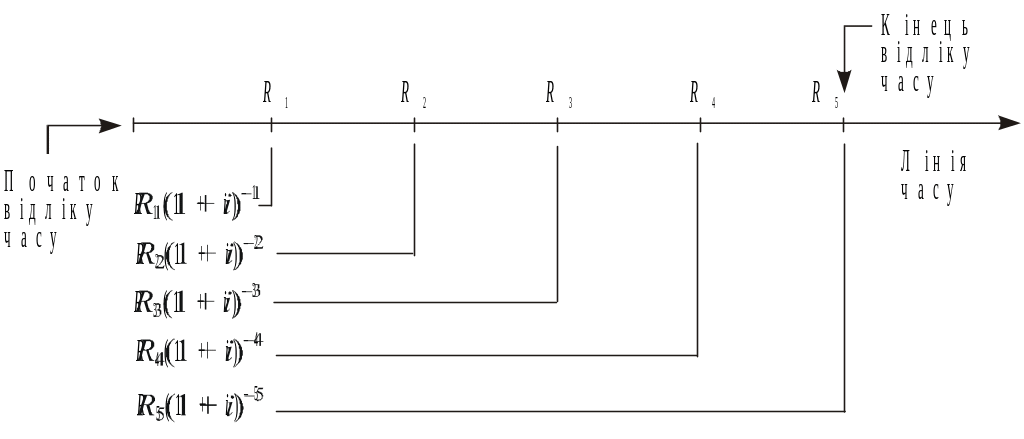
Рис. 1. Розрахунок сучасної величини ренти

Річна рента з нарахуванням відсотків m разів на рік.

.

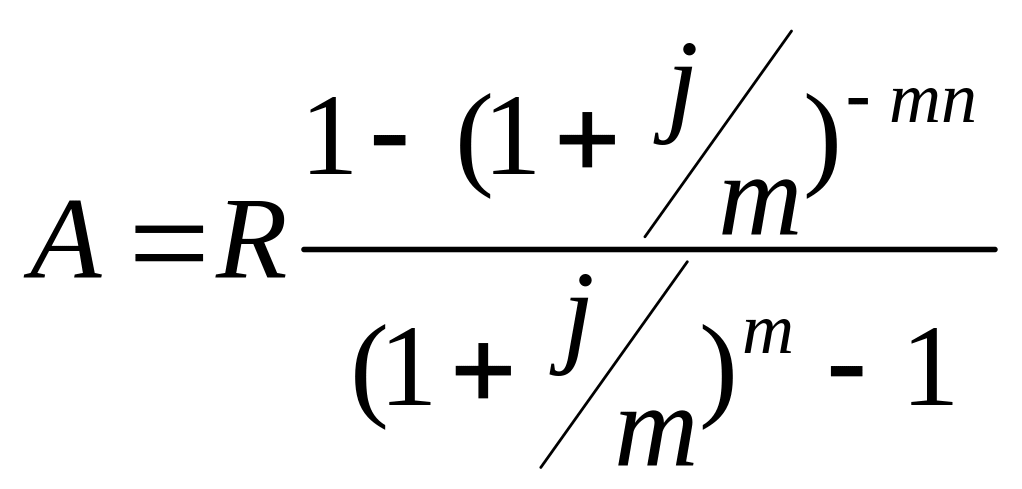Якщо платежі здійснюються не один, а р разів на рік, а відсотки нараховуються один раз на рік, то коефіцієнт приведення має вигляд:

,

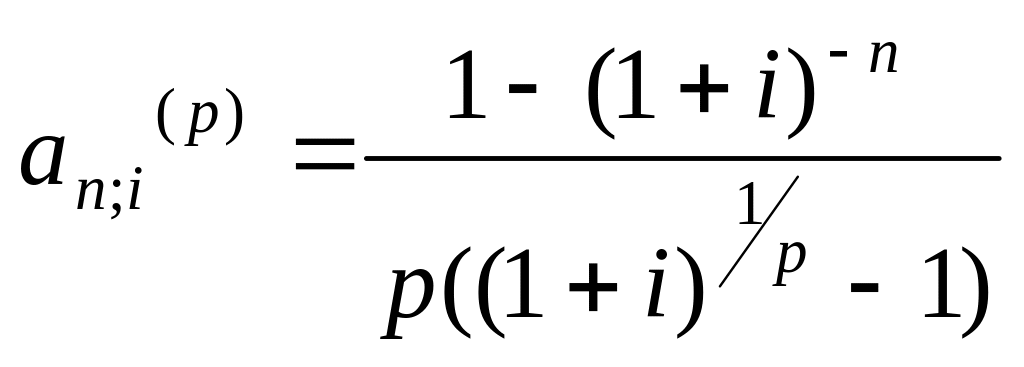а сучасна величина ренти розраховується за формулою:

.

Загальний випадок знаходження сучасної величини ренти, коли відсотки нараховуються m разів, виплати відбуваються р-разів на рік, а :

.

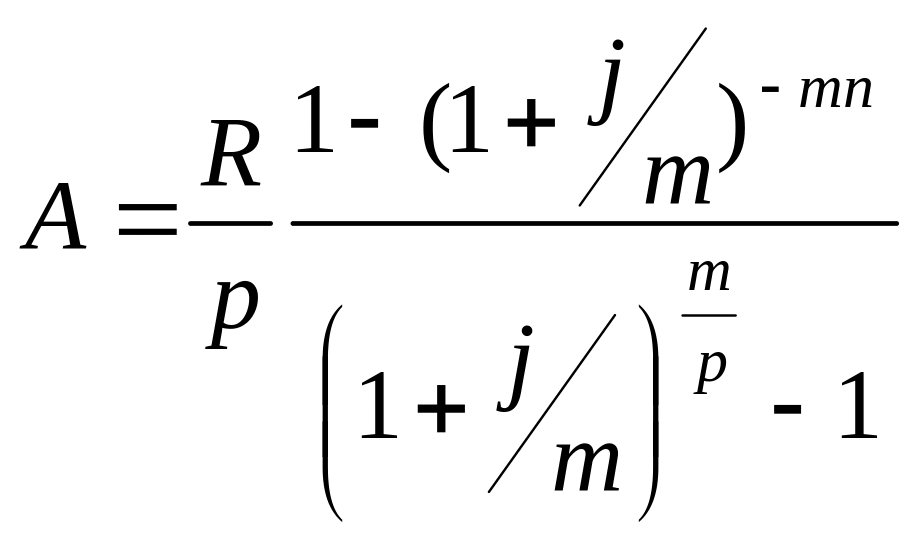Сучасну величину ренти можна отримати шляхом дисконтування нарощеної суми, тобто . Нарощену суму можна також отримати за значенням сучасної величини, тобто S = A(1 + i)ⁿ.

Вічна рента — це послідовність необмеженого числа платежів, які сплачуються протягом нескінченої кількості років.

Коефіцієнт приведення вічної ренти:

.

Формула сучасної величини вічної ренти має такий вигляд:

.

Якщо сума боргу визначена на якийсь момент у майбутньому і передбачається, що борг буде сплачено шляхом створення спеціального фонду на основі послідовних внесків протягом n років при нарахуванні на них відсотків за ставкою і, член ренти необхідно визначити на основі формул, які характеризують нарощену суму S:

.

Якщо поточний борг сплачується послідовними платежами, сума боргу дорівнює сучасній величині ренти, то член ренти визначається за такою формулою:

.

Розрахунок строку ренти здійснюється шляхом перетворення формул нарощеної або сучасної величини ренти.

Якщо рента річна і відсотки капіталізуються за річною ставкою і, то:

; ;

; .

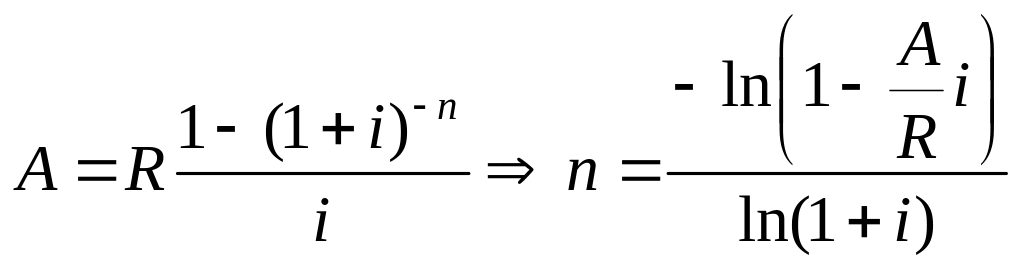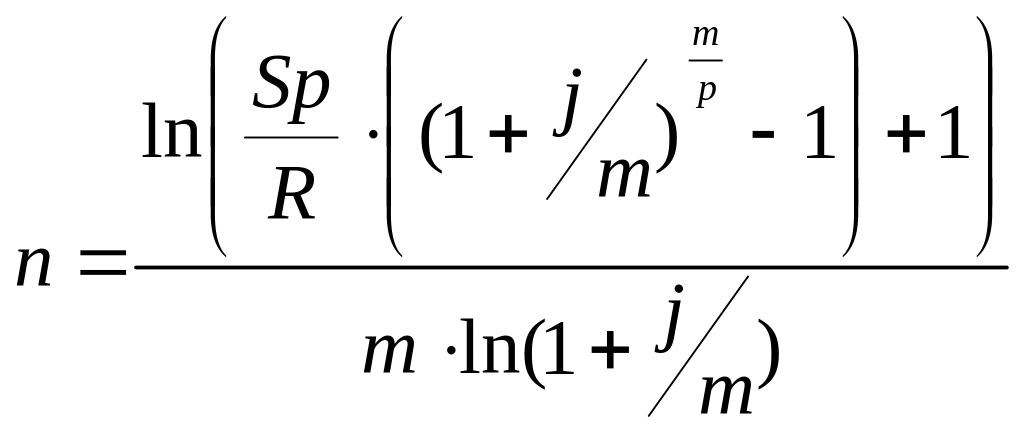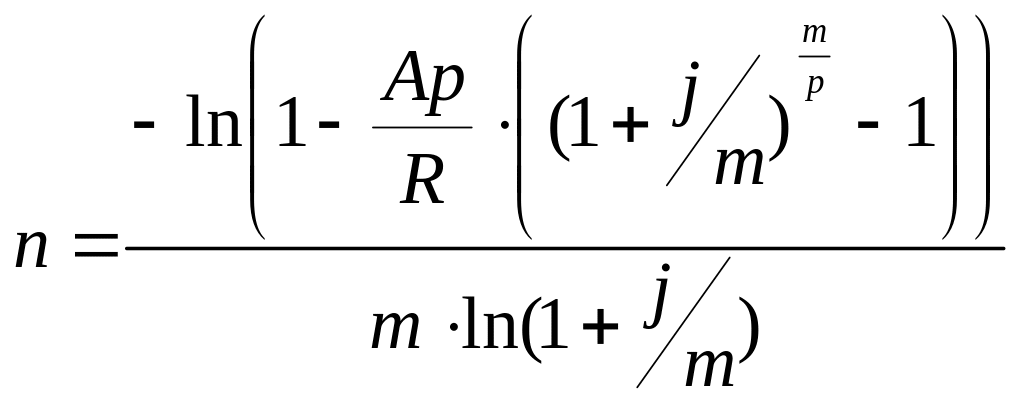Конверсія фінансових рент

Конверсією фінансових рент називається заміна потоку рентних платежів іншим платежем. У простому вигляді зміна умов ренти полягає в заміні ренти одночасним платежем. Також кілька рент можуть бути об’єднані в одну.

Якщо передбачається, що конверсія рент не повинна призводити до зміни фінансових наслідків для кожної сторони, то вона повинна відповідати принципу фінансової еквівалентності.

Серед різновидів конверсій можна виокремити такі: викуп ренти, відстрочка платежів, консолідація боргів.

Викуп ренти передбачає заміну одноразовим платежем усіх розподілених у часі платежів (наприклад, компенсація фонду, який створюється шляхом внесків або відрахувань). Згідно з принципом фінансової еквівалентності, викуп ренти — це виплата сучасної величини цієї ренти на даний момент.

Відстрочка платежів — це заміна одноразового платежу фінансовою рентою, тобто надання кредиту. Для збереження принципу фінансової еквівалентності сучасну величину ренти прирівнюють до величини платежу, який замінюється. Тоді за заданою сучасною величиною визначають розмір члена ренти та кількість платежів або термін ренти.

Приклад. Вартість партії товарів 100 тис. грн., що сплачується протягом трьох років. Кредит надається під 10 % річних платежів, які вносяться кожні півроку. Покупцеві надана відстрочка на три місяці, при цьому відсотки за час відстрочки приєднуються до вартості товарів. Як здійснюватиметься погашення кредиту?

Розв’язання: Спочатку необхідно визначити вартість товарів на кінець відстрочки:

Ця сучасна величина повинна бути сплачена за три роки.

Консолідація ренти — це об’єднання кількох рент в одну. Принцип фінансової еквівалентності у даному разі передбачає виконання такої рівності:

,

де А — сучасна величина рент, які замінюються; A_q — сучасна величина q-ї ренти (q = 1, 2, .., k).

При об’єднанні рент можуть виникнути найрізноманітніші задачі, зокрема: а) визначення розміру члена об’єднаної ренти; б) визначення терміну об’єднаної ренти. В обох випадках повинні бути задані інші параметри рент.