
- •Курсовая работа на тему: «Автоматизация рабочего места мастера колесно-роликого участка»
- •Содержание
- •1. Структурная схема арм 3
- •1.7. Структурная схема арм 7
- •2. Техническое обеспечение арм 8
- •3. Программное обеспечение арм 10
- •4. Математическое обеспечение арм: Выбор оптимальных стратегий 15
- •5. Математическое обеспечение арм: Моделирование производственных процессов 21
- •6. Математическое обеспечение арм: Экспертные системы и модели экспертизы
- •Введение
- •1. Структурная схема арм
- •1.1Назначение подразделений
- •1.2. Должностные обязанности руководителя (работника) подразделения
- •1.3. Назначение и основные задачи арм
- •1.4. Технические требования к арм
- •1.5. Выбор режима работы арм (индивидуальное, сетевое, индивидуально-сетевое)
- •1.6. Схема арм с учетом его режима работы
- •1.7. Структурная схема арм
- •2. Техническое обеспечение арм
- •2.1. Требования к техническому обеспечению арм
- •2.2. Структурная схема комплекса технических средств арм
- •2.3. Схема размещения оборудования
- •2.4. Критерии выбора параметров технических средств арм для офисной конфигурации.
- •2.5. Формирование вариантов конфигураций технических средств арм. Формулы конфигураций
- •3. Программное обеспечение арм
- •3.1 Общее программное обеспечение арм
- •3.2. Функциональное программное обеспечение
- •3.3. Перечень выбранного типового по и узко-ориентированных программ
- •3.4. Методика определения технико-экономического критерия конкурентоспособности арм
- •3.5. Выбор оптимального варианта арм. Программа определения конкурентоспособности
- •4. Математическое обеспечение арм: Выбор оптимальных стратегий
- •4.1. Классификация моделей поиска оптимальных стратегий
- •Методика расчета выигрыша (дохода) и параметров проектных вариантов машин
- •4.2. Формулировка задачи поиска оптимальных стратегий в соответствии с вариантом Выбор оптимальной модели машины
- •4.3. Алгоритм расчета и программа. Результаты расчетов. Выводы.
- •Математическое обеспечение арм: Моделирование производственных процессов
- •Модели вагоноремонтного производства
- •Моделирование случайных процессов по методу Монте-Карло
- •5.2. Постановка задачи построения математической модели в соответствии с вариантом
- •6. Математическое обеспечение арм: Экспертные системы и модели экспертизы производства
- •6.1. Классификация и назначение экспертных систем Классификация экспертных систем
- •6.2. Структурная схема экспертной системы Структурная схема аэс
- •6.3. Постановка и описание задачи экспертизы производства в соответствии с вариантом Метод экспертных оценок (метод простого ранжирования)
- •4.1. Технология решения задач ранжирования признаков и определения коэффициентов весомости
- •6.4. Разработка программы автоматизации экспертизы. Результаты расчетов. Выводы.
- •Список литературы
- •1. М.М. Болотин. Сборник электронных пособий по дисциплине:
3.3. Перечень выбранного типового по и узко-ориентированных программ

3.4. Методика определения технико-экономического критерия конкурентоспособности арм
Численные значения технико-экономического критерия можно определять по формуле:
 ,
,
где
 -
интегральный показатель конкурентоспособности
по техническим параметрам;
-
интегральный показатель конкурентоспособности
по техническим параметрам;
 количество,
исследуемых технических параметров;
количество,
исследуемых технических параметров;
 коэффициент
весомости
коэффициент
весомости
 го
технического параметра:
го
технического параметра:
 абсолютный
вес
го
технического параметра;
абсолютный
вес
го
технического параметра;
 эмпирический
коэффициент (
эмпирический
коэффициент ( .
.
В качестве технических параметров можно, например, принимать следующие характеристики системного блока и монитора:
 тактовая
частота (
тактовая
частота ( );
);
 объем
оперативной памяти (
объем
оперативной памяти ( );
);
 средняя
наработка до отказа (
средняя
наработка до отказа ( );
);
 объем
памяти жесткого диска (
объем
памяти жесткого диска ( );
);
 объем
памяти видеокарты (
объем
памяти видеокарты ( );
);
 шум вентиляторов
(
шум вентиляторов
(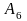 );
);
 время отклика (
время отклика ( ) и др. (набор
параметров выбирает разработчик АРМ);
) и др. (набор
параметров выбирает разработчик АРМ);
 или
или
 - относительный показатель
конкурентоспособности, сравниваемых
параметров системного блока или монитора
(первое
соотношение применяется для показателей,
имеющих тенденцию роста, а второе –
снижения: первые пять показателей имеют
тенденцию роста, а два последних –
тенденцию снижения).
Увеличение
относительного показателя должно
соответствовать улучшению качества
продукта (АРМ);
- относительный показатель
конкурентоспособности, сравниваемых
параметров системного блока или монитора
(первое
соотношение применяется для показателей,
имеющих тенденцию роста, а второе –
снижения: первые пять показателей имеют
тенденцию роста, а два последних –
тенденцию снижения).
Увеличение
относительного показателя должно
соответствовать улучшению качества
продукта (АРМ);
 абсолютное значение
го
технического параметра для проектируемого
варианта;
абсолютное значение
го
технического параметра для проектируемого
варианта;
 абсолютное
значение
го
технического параметра для базовой
модели конфигурации АРМ (базовая модель
конфигурации АРМ и ее характеристики
задаются до начала расчетов).
абсолютное
значение
го
технического параметра для базовой
модели конфигурации АРМ (базовая модель
конфигурации АРМ и ее характеристики
задаются до начала расчетов).
 интегральный
показатель конкурентоспособности по
экономическим параметрам (см. материалы
лекции или работу [1]);
интегральный
показатель конкурентоспособности по
экономическим параметрам (см. материалы
лекции или работу [1]);
 коэффициент
весомости
коэффициент
весомости
 го
экономического параметра;
го
экономического параметра;
 среднегодовые
затраты на разработку АРМ (
среднегодовые
затраты на разработку АРМ ( ),
приобретение технических и программных
средств (
),
приобретение технических и программных
средств ( ),
техническое обслуживание и ремонт АРМ
(
),
техническое обслуживание и ремонт АРМ
( )
соответственно для проектируемого и
базового вариантов АРМ.
)
соответственно для проектируемого и
базового вариантов АРМ.
Показатель средней наработки до отказа, как правило, в технических документах на ПЭВМ не указывается. Этот параметр можно приближенно определить по величине срока гарантии на элементы системного блока. Среднее значение этого параметра можно принимать 4422 ч, минимальное – 3368 ч, максимальное – 5578 ч.
Стоимость системного блока проектного варианта АРМ при увеличении показателя наработки до отказа по сравнению со средним значением можно определять по формуле:
 ,
,
где
 средняя
наработка до отказа для
го
варианта СБ и средняя наработка до
отказа
средняя
наработка до отказа для
го
варианта СБ и средняя наработка до
отказа
 =4422
ч.;
=4422
ч.;
 стоимость
проектного варианта СБ в зависимости
от параметров его комплектующих.
стоимость
проектного варианта СБ в зависимости
от параметров его комплектующих.
3.5. Выбор оптимального варианта арм. Программа определения конкурентоспособности

Вывод: Лучший вариант – АРМ3

4. Математическое обеспечение арм: Выбор оптимальных стратегий
4.1. Классификация моделей поиска оптимальных стратегий
Классификация моделей поиска оптимальных стратегий
Элементы теории поиска оптимальных стратегий
Различают три вида моделей поиска оптимальных стратегий:
Модели принятия решений в условиях определенности;
Модели принятия решений в условиях риска;
Модели принятия решений в условиях стохастической неопределенности.
В качестве критериев для задач с полной определенностью принимают минимум удельных приведенных затрат, максимум прибыли или максимум технико-экономического критерия конкурентоспособности.
Для моделей принятия решений в условиях риска считается, что каждая стратегия может привести к одному из множества исходов, отличающихся вероятностью появления (вероятности появления ситуаций или событий считаются известными).
Решение задач осуществляют в форме матрицы выигрышей или рисков (в строках первого столбца располагаются стратегии, а в следующих столбцах первой строки ситуации и вероятности их появления, в каждой клеточке матрицы на пересечении ой строки и го столбца записывается выигрыш или риск). В качестве критериев оптимизации применяют:
«оптимизация в среднем»
 -
максимальное значение среднего выигрыша;
-
максимальное значение среднего выигрыша;
критерий Лапласа (принцип
недостаточного основания Лапласа:
вероятности всех событий полагаются
одинаковыми)
 - максимальное значение суммарного
выигрыша;
- максимальное значение суммарного
выигрыша;
где
 расчетный
доход для
стратегии
и
ой
ситуации;
расчетный
доход для
стратегии
и
ой
ситуации;
 вероятность
появления
ой
ситуации;
вероятность
появления
ой
ситуации;
максиминный критерий
Вальда:
 ;
;
критерий оптимизма
– пессимизма Гурвица:
 (
( коэффициент
везучести
коэффициент
везучести
 );
);
критерий максимакса
– критерий крайнего оптимизма
 .
.
«минимальный средний риск»:
 ;
;
минимаксный критерий
Сэвиджа:
 .
.
Под риском понимается разность между максимальным и текущим доходами для рассматриваемой ситуации:
 .
.
Для решения задач поиска оптимальных стратегий можно применить интегрированный пакет Microsoft Office/ Microsoft Excel.
